20. Численное интегрирование. Формула центральных прямоугольников. Геометрическая иллюстрация, элементарная и составная формулы, оценка погрешности.

Требуется найти

В прикладных задачах этот интеграл может выражать площадь, объём, работу переменной силы и т.д.

Формулы прямоугольников.

Для простоты шаг – будем считать постоянным.

Элементарная квадратурная формула прямоугольников:

Составная квадратурная формула прямоугольников (центральных прямоугольников):

Формула левых прямоугольников:

Формула правых прямоугольников:

Обозначение 6.1.

Оценка: Пусть функция дважды непрерывно дифференцируема на отрезке . Тогда

Погрешность формулы прямоугольников

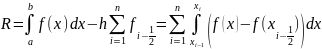
21. Численное интегрирование. Формула трапеций. Геометрическая иллюстрация, элементарная и составная формулы, оценка погрешности.

Требуется найти

В прикладных задачах этот интеграл может выражать площадь, объём, работу переменной силы и т.д.

Формула трапеций.

Элементарная квадратурная формула трапеций:

Составная квадратурная формула трапеций:

Теорема 6.2. Пусть функция дважды непрерывно дифференцируема на отрезке . Тогда

(6.7)

22. Численное интегрирование. Формула Симпсона. Элементарная и составная формулы, оценка погрешности (без док-ва).

Требуется найти

В прикладных задачах этот интеграл может выражать площадь, объём, работу переменной силы и т.д.

Формула Симпсона.

Элементарная квадратурная формула Симпсона:

Идея построения. Это так называемая формула парабол. На каждом элементарном отрезке строится интерполяционный многочлен второй степени (парабола), затем этот многочлен интегрируется.

Составная квадратурная формула Симпсона:

Теорема 6.3. Пусть функция четырежды непрерывно дифференцируема на отрезке . Тогда

(6.9)

Замечание 6.1. Оценки (6.5), (6.7), (6.9) означают, что формулы прямоугольников и трапеция имеют второй порядок точности относительно , а формула Симпсона – четвёртый порядок точности. Из тех же оценок следует, что формулы прямоугольников и трапеций точны для многочленов первой степени, а формула Симпсона – для многочленов третьей степени.

23. Численное интегрирование. Понятие о формулах Ньютона-Котеса. Правило Рунге апостериорной оценки погрешности.

Требуется найти

В прикладных задачах этот интеграл может выражать площадь, объём, работу переменной силы и т.д.

Формулы Ньютона-Котеса.

Идея построения. Интеграл представляют в виде суммы интегралов по элементарным отрезкам. На каждом таком отрезке подынтегральная функция аппроксимируется легко интегрируемой функцией.

В случае, когда аппроксимация осуществляется с помощью интерполяционных многочленов, построенных на основе равноотстоящих значений , имеем квадратурные формулы Ньютона-Котеса:

Теорема 6.4. Пусть функция имеет на отрезке непрерывную производную порядка . Тогда для погрешности формулы (6.10) справедлива оценка

где .

Без доказательства.

Замечание 6.2. Оценки (6.11) означает, что формула имеют -й порядок точности относительно , и, что формула точна для многочленов степени .

Замечание 6.3. Формулы прямоугольников, трапеций и Симпсона – частный случай формулы Ньютона-Котеса.