Контрольное задание по дисциплине «Теория вероятностей и математическая статистика» Вариант 4

1. На диаграмме Венна событие изображается…

2. Вероятность события есть неотрицательное число, то есть

а) б) в) г)

д) е) ж) з)

3. Известны вероятности несовместных событий , , . Указать вероятности событий, которые образуют полную группу

а) , , б) , ,

в) , , г) , ,

4. Даны вероятности событий , и : , , . Укажите верное утверждение

а) и независимы и несовместны б) и независимы и совместны

в) и зависимы и совместны г) и зависимы и несовместны

5. Внутрь правильного треугольника наудачу брошена точка. Вероятность того, что точка окажется внутри треугольника, вершины которого являются серединами сторон исходного треугольника, равна… а) б) в) г)

6. Сколько существует вариантов рассаживания 6 гостей на 6 стульях?

а) 36 б) 180 в) 720 г) 300

7. На плоскости даны 10 точек, причем три из них не лежат на одной прямой. Сколько существует лучей с началом в любой из данных точек, проходящих через любую другую из данных точек?

а) 90 б) 360 в) 500 г) 100

8. На полке стоят 12 книг. Надо взять 5 книг. Сколькими способами это можно сделать?

а) 792 б) 17 в) 60 г) 300

9. В игральной колоде 36 карт. Наугад выбирается одна карта. Вероятность того, что эта карта – туз, равна… а) б) в) г)

10. Катя и Аня пишут диктант. Вероятность того, что Катя допустит ошибку равна 0,6, вероятность ошибки у Ани 0,4. Вероятность того, что обе девочки напишут диктант без ошибок, равна…

а) 0,25 б) 0,4 в) 0,48 г) 0,24

11. Среди 6 ламп имеется 2 неисправных. Лампы включают по очереди до выявления обеих неисправных. Вероятность того, что эксперимент закончится на 3 лампе, равна…

а) 0,2 б) 0,33 в) 0,66 г)

12. В урне 2 белых и 4 черных шара. Извлекают по очереди два шара, причем после первого извлечения шар возвращается в урну. Вероятность того, что оба шара белые, равна…

а) б) в) г)

13. В урне 6 белых шаров и 8 черных. Из урны извлекают шары до появления белого шара (без возвращения). Вероятность того, что будет проведено всего 3 опыта, равна…

а) 1 б) 0,9 в) 0,21 г) 0,79

14. Бросают игральную кость до появления на грани кубика 3 очков. Вероятность того, что эксперимент закончится на втором броске, равна…

а) б) в) г)

15. По цели производится 4 выстрела. Вероятность попадания в одном выстреле равна . Вероятность того, что в цель попали ровно 2 раза, равна:

а) 0,8 б) 0,3456 в) 0,1536 г) 0,4

16. Вероятность того, что в результате пяти бросков игральной кости нечетное количество очков выпадет не менее 4 раз, равна…

а) 0,3125 б) 0,2645 в) 0,1875 г) 0,5

17. Событие может наступить лишь при условии появления одного из двух несовместимых событий и , образующих полную группу событий. Известны вероятность и условные вероятности , . Вероятность события равна…

а) б) в) г)

18. В первой урне 2 черных и 3 белых шаров. Во второй урне 1 черный и 2 белых шара. Из наудачу выбранной урны извлекают один шар. Вероятность того, что шар белый равна…

а) б) в) г)

19. Один из двух стрелков произвёл выстрел по мишени. Вероятности попадания для каждого стрелка соответственно равны , . Цель поражена. Вероятность того, что стрелял первый стрелок, равна…

а) б) в) г)

20. Имеется пять винтовок, три из которых снабжены оптическим прицелом. Вероятность попадания в цель при выстреле из винтовки с оптическим прицелом, равна 0,95, для винтовки без оптического прицела – 0,7. Цель не поражена. Вероятность того, что выстрел был из винтовки без оптического прицела, равна…

а) б) в) 0,2 г) 0,8

2 1. Дан графический закон распределения дискретной случайной величины (многоугольник распределения). Ряд распределения случайной величины имеет вид…

а) б)

в) г)

22. Дискретная случайная величина принимает значения -1, 1, 2 с соответствующими вероятностями , 0,5, 0,3. Математическое ожидание случайной величины равно…

а) 1 б) 0,9 в) 1,9 г) 1,3

23. Дан ряд распределения случайной величины:

	-2		6
		0,3	0,4

Мода случайной величины равна…

а ) 6 б) 0,5 в) г) 0,3

24. Дан график функции распределения случайной величины

со значениями и . Вероятность значения равна….

а) 0,8 б) 0,2 в) 0,6 г) 0,4

25. Дан ряд распределения случайной величины :

	1	4	5	8
	0,3			0,4

Математическое ожидание . Вероятность равна…

а) 0,2 б) 0,1 в) 0,4 г) 0,3

26. Дан ряд распределения случайной величины :

	2

. Математическое ожидание , дисперсия . Значение вероятности равно…

а) 0,6 б) 0,4 в) 0,5 г) 0,3

27. В урне 2 белых и 4 черных шара. Шары извлекаются из урны без возвращения до появления черного шара. Случайная величина – количество извлеченных белых шаров. Ряд распределения случайной величины имеет вид…

а) б) в) г)

28. Стрелок производит 30 выстрелов по мишени. Вероятность попадания при одном выстреле 0,6. Случайная величина – количество промахов. Математическое ожидание случайной величины равно…

а) 12 б) 18 в) 15 г) 20

29. Игральную кость бросают 36 раз. Случайная величина – количество выпавших «двоек». Дисперсия случайной величины равна…

а) б) в) г)

30. Случайная величина задана функцией распределения

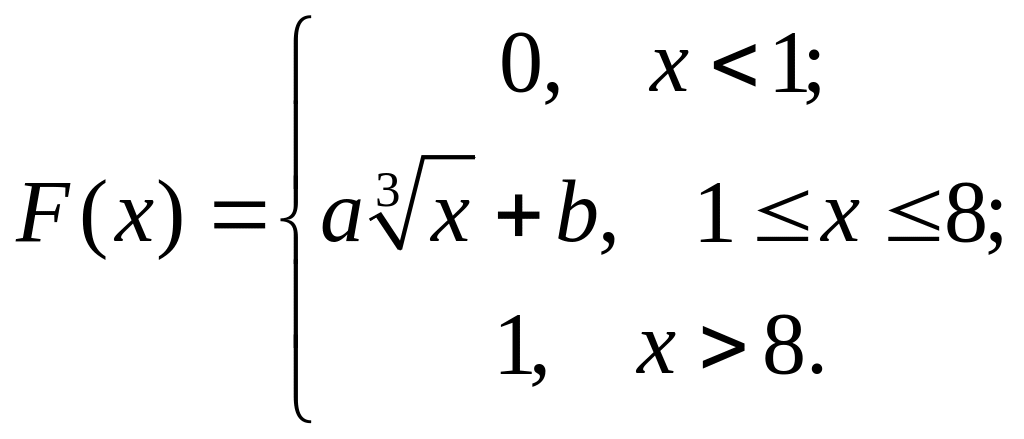
Параметр равен…

а) 8 б) 1 в) -1 г) 0

31. Соответствие между возможными значениями случайной величины и их вероятностями называют…

a) функцией распределения дискретной случайной величины

б) законом больших чисел

в) законом распределения дискретной случайной величины

г) законом случайной величины

3 2. График функции плотности распределения вероятностей случайной величины имеет вид

Тогда значение равно…

а) б) в) г)

33. Случайная величина распределена по равномерному закону на отрезке . Математическое ожидание случайной величины равно…

а) б) в) г)

34. Случайная величина распределена по равномерному закону на отрезке [5; 7]. Вероятность попадания случайной величины в интервал равна…

а) б) в) г)

35. Случайная величина распределена по экспоненциальному закону с параметром . Функция распределения вероятностей случайной величины имеет вид…

а) б)

в) г)

36. Случайная величина распределена по показательному закону с параметром . Дисперсия случайной величины равна…

а) 0,5 б) 0,25 в) 4 г) 25

3 7. График функции плотности распределения вероятностей случайной величины имеет вид

5 Математическое ожидание случайной величины

равно…

а) 0,2 б) 0,04 в) 4 г) 0,25

38. Случайная величина распределена по экспоненциальному закону с параметром . Вероятность попадания случайной величины в интервал равна…

а) б) в) г)

39. Закон распределения случайной величины задан функцией плотности . Среднее квадратичное отклонение случайной величины равно…

а) 1 б) 0 в) 9 г) 3

40. Функция плотности распределения вероятностей случайной величины имеет вид . Точки перегиба кривой Гаусса…

а) 1; 9 б) 1; 3 в) 3; 9 г) 0; 5