
- •Уважаемые студенты!!!! Информация к .. Исполнению и размышлению.
- •Контрольное задание по дисциплине «Теория вероятностей и математическая статистика» Вариант 1
- •Контрольное задание по дисциплине «Теория вероятностей и математическая статистика» Вариант 2
- •1. На диаграмме Венна событие изображается…
- •3. Известны вероятности несовместных событий , , . Указать вероятности событий, которые образуют полную группу
- •4. Даны вероятности событий , и : , , . Укажите верное утверждение
- •Контрольное задание по дисциплине «Теория вероятностей и математическая статистика» Вариант 3
- •1. На диаграмме Венна событие изображается…
- •3. Известны вероятности несовместных событий , , . Указать вероятности событий, которые образуют полную группу
- •4. Даны вероятности событий , и : , , . Укажите верное утверждение
- •Контрольное задание по дисциплине «Теория вероятностей и математическая статистика» Вариант 4
- •1. На диаграмме Венна событие изображается…
- •3. Известны вероятности несовместных событий , , . Указать вероятности событий, которые образуют полную группу
- •4. Даны вероятности событий , и : , , . Укажите верное утверждение
- •Контрольное задание по дисциплине «Теория вероятностей и математическая статистика» Вариант 5
- •1. На диаграмме Венна событие изображается…
- •3. Известны вероятности несовместных событий , , . Указать вероятности событий, которые образуют полную группу
- •4. Даны вероятности событий , и : , , . Укажите верное утверждение
- •Контрольное задание по дисциплине «Теория вероятностей и математическая статистика» Вариант 6
- •1. На диаграмме Венна событие изображается…
- •3. Известны вероятности несовместных событий , , . Указать вероятности событий, которые образуют полную группу
- •4. Даны вероятности событий , и : , , . Укажите верное утверждение
- •Контрольное задание по дисциплине «Теория вероятностей и математическая статистика» Вариант 7
- •1. На диаграмме Венна событие изображается…
- •3. Известны вероятности несовместных событий , , . Указать вероятности событий, которые образуют полную группу
- •4. Даны вероятности событий , и : , , . Укажите верное утверждение
- •Контрольное задание по дисциплине «Теория вероятностей и математическая статистика» Вариант 82
- •1. На диаграмме Венна событие изображается…
- •3. Известны вероятности несовместных событий , , . Указать вероятности событий, которые образуют полную группу
- •4. Даны вероятности событий , и : , , . Укажите верное утверждение
- •Контрольное задание по дисциплине «Теория вероятностей и математическая статистика» Вариант 9
- •1. На диаграмме Венна событие изображается…
- •3. Известны вероятности несовместных событий , , . Указать вероятности событий, которые образуют полную группу
- •4. Даны вероятности событий , и : , , . Укажите верное утверждение
- •Контрольное задание по дисциплине «Теория вероятностей и математическая статистика» Вариант 10
- •1. На диаграмме Венна событие изображается…
- •3. Известны вероятности несовместных событий , , . Указать вероятности событий, которые образуют полную группу
- •4. Даны вероятности событий , и : , , . Укажите верное утверждение
Уважаемые студенты!!!! Информация к .. Исполнению и размышлению.
1. Контрольная работа выполняется на листах формата А;4 (стандартных).
2. На каждое задание должно быть представлено РЕШЕНИЕ,
а не просто выбор ответа.
3. Если в задании вопрос теоретического плана, необходимо
сначала привести определение или формулировку свойства,
затем указать правильный вариант ответа или несколько, если это
указано в условии.
4.Работы, выполненные не по указанным правилам, признаются незачтенными
и будут возвращены для повторного выполнения.
В этом случае экзамен для Вас не состоится.
5.Самостоятельно выполненная контрольная работа –
залог Вашего успеха на предстоящем экзамене.
Напоминаю,
вариант определяется по последней цифре номера зачетной книжки.
С надеждой на понимание.
Борисова Е.В,
ТвГТУ, Тверь, 2012
Контрольное задание по дисциплине «Теория вероятностей и математическая статистика» Вариант 1
1.
На диаграмме Венна событие
![]() изображается…
изображается…
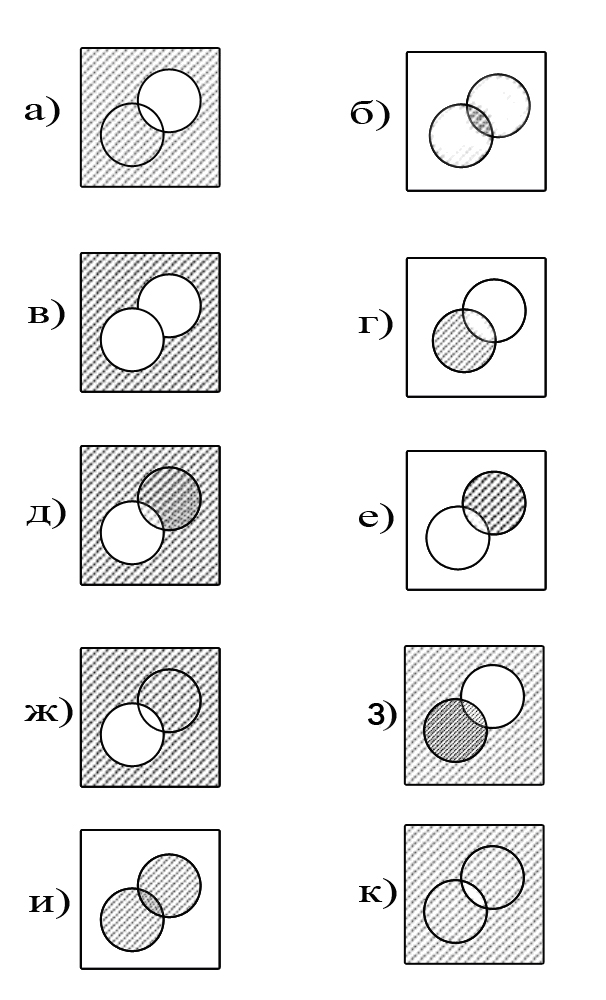
2. Вероятность случайного события равна…
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
д)
![]() е)
е)
![]() ж)
ж)
![]() з)
з)
![]()
3.
Известны вероятности несовместных
событий
![]() ,
,
![]() ,
,
![]() .
Указать вероятности событий, которые
образуют полную группу
.
Указать вероятности событий, которые
образуют полную группу
а)
![]() ,
,
![]() ,
,
![]() б)
б)
![]() ,
,
![]() ,
,
в)
,
,
г)
![]() ,
,
![]() ,
,
![]()
4. Даны
вероятности событий
,
и
![]() :
:
![]() ,
,
![]() ,
,
![]() .
Укажите верное утверждение
.
Укажите верное утверждение
а) и независимы и несовместны б) и независимы и совместны
в) и зависимы и совместны г) и зависимы и несовместны
5. Внутрь квадрата наудачу брошена точка. Вероятность того, что точка окажется внутри треугольника, вершины которого являются серединами трех сторон квадрата, равна…
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
6. Сколькими способами можно расставить 4 различные книги на книжной полке?
а) 24 б) 4 в) 16 г) 20
7. В футбольной команде 11 человек. Необходимо выбрать капитана и его заместителя. Сколькими способами это можно сделать?
а) 22 б) 11 в) 150 г) 110
8. Имеются помидоры, огурцы и лук. Сколько различных салатов можно приготовить, если в каждый салат должно входить 2 различных вида овощей?
а) 3 б) 6 в) 2 г) 1
9. В урне находятся 45 шариков, из которых 17 белых. Потеряли 2 белых шарика. Вероятность того, что выбранный наугад шарик будет белым равна…
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
10. Бросают два игральных кубика. Вероятность того, что на выпавших гранях четные значения, равна…
а) 0,25 б) 0,33 в) 0,5 г) 0,125
11. Среди 6 ламп имеется одна неисправная. Лампы включают по очереди до выявления неисправной. Вероятность того, что эксперимент закончится на 4 лампе, равна…
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
12. В урне 2 белых и 1 черный шар. Извлекают по очереди два шара, причем после первого извлечения шар возвращается в урну. Вероятность того, что оба шара белые, равна…
а)
б)
в)
![]() г)
г)
![]()
13. Вероятность появления некоторого события в одном испытании равна 0,3. Опыты проводятся до появления указанного события. Вероятность того, что придется проводить третий опыт, равна…
а) 1 б) 0,9 в) 0,21 г) 0,49
14. Бросают игральную кость до появления на грани кубика 2 очков. Вероятность того, что эксперимент закончится на третьем броске, равна…
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
15. По
цели производится 4 выстрела. Вероятность
попадания в одном выстреле равна
![]() .
Вероятность того, что в цель попали
ровно 3 раза, равна:
.
Вероятность того, что в цель попали
ровно 3 раза, равна:
а) 0,4116 б) 0,2646 в) 0,0756 г) 0,6
16. Вероятность того, что в результате четырех бросков монеты выпадет более 2 раз орел, равна…
а) 0,3125 б) 0,2645 в) 0,125 г) 0,5
17.
Событие
может наступить лишь при условии
появления одного из двух несовместимых
событий
![]() и
и
![]() ,
образующих полную группу событий.
Известны вероятность
,
образующих полную группу событий.
Известны вероятность
![]() и условные вероятности
и условные вероятности
![]() ,
,
![]() .
Вероятность события
равна…
.
Вероятность события
равна…
а) 0,66 б) 0,3125 в) 0,42 г) 0,4375
18. В первой урне 2 черных и 3 белых шаров. Во второй урне 2 черных и 1 белый шаров. Из наудачу выбранной урны извлекают один шар. Вероятность того, что шар черный равна…
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
19.
Один из двух стрелков произвёл выстрел
по мишени. Вероятности попадания для
каждого стрелка соответственно равны
![]() ,
,
![]() .
Цель поражена. Вероятность того, что
стрелял второй стрелок, равна… а)
б)
.
Цель поражена. Вероятность того, что
стрелял второй стрелок, равна… а)
б)
![]() в)
в)
![]() г)
г)
![]()
20.
Имеется пять винтовок, три из которых
снабжены оптическим прицелом. Вероятность
попадания в цель при выстреле из винтовки
с оптическим прицелом, равна 0,95, для
винтовки без оптического прицела –
0,7. Вероятность того, что цель поражена
из винтовки с оптическим прицелом,
равна… а)
![]() б)
б)
![]() в) 0,2 г) 0,8
в) 0,2 г) 0,8
2 1.
Дан графический закон распределения
дискретной случайной величины
(многоугольник распределения). Ряд
распределения случайной величины имеет
вид…
1.
Дан графический закон распределения
дискретной случайной величины
(многоугольник распределения). Ряд
распределения случайной величины имеет
вид…
а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
22. Дискретная
случайная величина принимает значения
2, 5, 9 с соответствующими вероятностями
0,3, 0,1,
![]() .
Математическое ожидание случайной
величины равно…
.
Математическое ожидание случайной
величины равно…
а) 5,5 б) 6,5 в) 7,5 г) 8
23. Дан ряд распределения случайной величины:
|
-4 |
1 |
3 |
5 |
|
0,1 |
0,3 |
|
0,2 |
Мода случайной величины равна…
а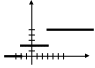 )
5 б) 3 в)
0,4 г)
0,3
)
5 б) 3 в)
0,4 г)
0,3
24. Дан
график функции распределения
![]() случайной величины
случайной величины
со значениями
![]() и
и
![]() .
Вероятность значения
равна…
.
Вероятность значения
равна…
а) 0,8 б) 0,2 в) 0,6 г) 0,4
25. Дан ряд распределения случайной величины :
|
1 |
4 |
5 |
8 |
|
|
0,1 |
|
0,4 |
Математическое
ожидание
![]() .
Вероятность
равна…
.
Вероятность
равна…
а) 0,2 б) 0,1 в) 0,4 г) 0,3
26. Дан ряд распределения случайной величины :
|
2 |
|
|
|
|
![]() .
Математическое ожидание
.
Математическое ожидание
![]() ,
дисперсия
,
дисперсия
![]() .
Значение случайной величины
равно…
.
Значение случайной величины
равно…
а) 3 б) 4 в) 5 г) 6
27. В урне 2 белых и 3 черных шара. Шары извлекаются из урны без возвращения до появления черного шара. Случайная величина – количество извлеченных белых шаров. Ряд распределения случайной величины имеет вид…
а)
![]() б)
б)
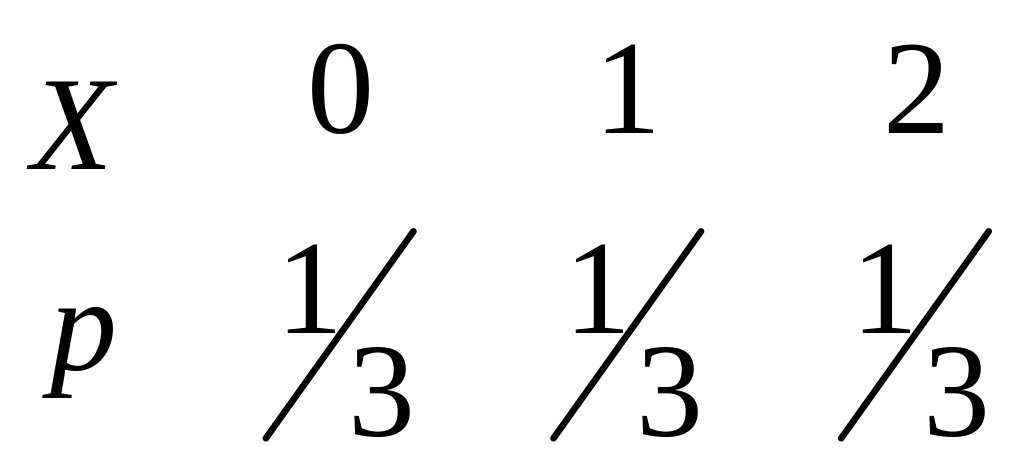 в)
в)
 г)
г)

28. Стрелок производит 30 выстрелов по мишени. Вероятность попадания при одном выстреле 0,4. Случайная величина – количество попаданий. Математическое ожидание случайной величины равно…
а) 12 б) 18 в) 15 г) 20
29. Игральную кость бросают 36 раз. Случайная величина – количество выпавших «двоек». Дисперсия случайной величины равна…
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
30.
Дана функция распределения случайной
величины
:
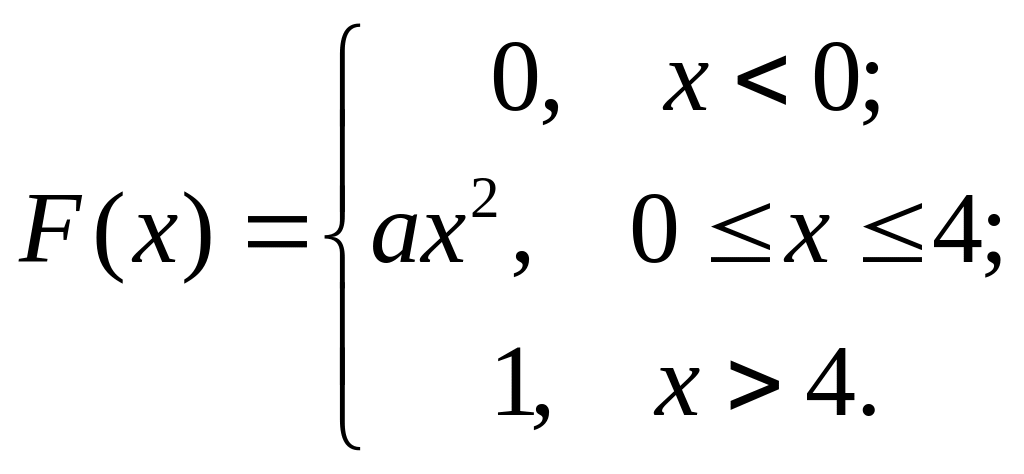
Параметр
![]() равен…
равен…
а) 8 б) 0,125 в) 0,04 г) 0,0625
31. Дисперсия постоянной величины равна…
a)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
3 2.
График
функции плотности распределения
вероятностей случайной величины
имеет вид
2.
График
функции плотности распределения
вероятностей случайной величины
имеет вид
Тогда значение равно…
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
33. Случайная
величина
распределена по равномерному закону
на отрезке
![]() .
Математическое ожидание случайной
величины равно…
.
Математическое ожидание случайной
величины равно…
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
34. Случайная
величина
распределена по равномерному закону
на отрезке [2; 10]. Вероятность попадания
случайной величины в интервал
![]() равна…
равна…
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
35. Случайная
величина
распределена по экспоненциальному
закону с параметром
![]() .
Функция распределения вероятностей
случайной величины имеет вид…
.
Функция распределения вероятностей
случайной величины имеет вид…
а)
![]() б)
б) ![]()
в)
![]() г)
г)
![]()
36. Случайная
величина
распределена по показательному закону
с параметром
![]() .
Дисперсия случайной величины равна…
.
Дисперсия случайной величины равна…
а) 0,5 б) 0,25 в) 4 г) 2
3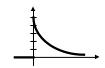 7.
График
функции плотности распределения
вероятностей случайной величины
имеет вид
7.
График
функции плотности распределения
вероятностей случайной величины
имеет вид
![]() Тогда
математическое ожидание случайной
Тогда
математическое ожидание случайной
величины равно…
а) 5 б) 0,2 в) 0,04 г) 25
38. Случайная
величина
распределена по экспоненциальному
закону с параметром
![]() .
Вероятность попадания случайной величины
в интервал
.
Вероятность попадания случайной величины
в интервал
![]() равна…
равна…
а)
![]() б)
б) ![]() в)
в)
![]() г)
г)
![]()
39. Закон
распределения случайной величины
задан функцией плотности
![]() .
Среднее квадратическое отклонение
случайной величины равно…
.
Среднее квадратическое отклонение
случайной величины равно…
а) 16 б) 5 в) 4 г) 2
40. Функция
плотности распределения вероятностей
случайной величины
имеет вид
![]() .
Точка максимума кривой Гаусса имеет
абсциссу…
.
Точка максимума кривой Гаусса имеет
абсциссу…
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
