3. Режими руху рідини. Число Рейнольдса

У 1883 р. англійський фізик Осборн Рейнольдс установив існування двох режимів руху рідин - ламінарного і турбулентного.

Змінюючи за допомогою крана витрату рідини, через прозору трубу лабораторної установки Рейнольдс спостерігав дві різні картини руху підфарбованої струмини рідини.

Два режими руху він назвав ламінарним (від латинського - шаровий) і турбулентним (від латинського - бурхливий, обурений). Це чисто зовнішні, візуальні відмінності двох режимів руху. Коло інженерного застосування цих відмінностей обмежене. Більш важливі енергетичні відмінності між ламінарним і турбулентним режимами Руху. Під час тубулентного руху окремі частки рідини рухаються не паралельно осі труби, а хаотично.

Аналізуючи вплив на режим руху різних параметрів, Рейнольдс запропонував характеризувати його безрозмірним критерієм, складеним з величин, що найбільше впливають на режим течії. Цей критерій називають критерієм Рейнольдса, або числом Рейнольдса. Для випадку напірної течії в круглих трубах

(2.13)

де V- середня швидкість;

d - внутрішній діаметр труби;

v - кінематичний коефіцієнт в'язкості.

З фізичної точки зору цей критерій характеризує співвідношення інерційних сил і сил тертя, зумовлених в'язкістю рідини.

У результаті численних дослідів з рідинами різної в'язкості і на трубах різного діаметра Рейнольдс зазначив два критичні значення критерію Re: нижнє критичне - Re_KpH^=::2320; верхнє критичне - Re_Kp =13800. При Re<Re_KpH течія ламінарна. У практичних розрахунках використовують, як правило, тільки Re_кр.н. Вважають, що якщо Re< Re_крН=2320, то буде ламінарний режим, а коли Re > Re_кр.в, то буде турбулентний. Причому, індекс "Н" опускають і пишуть так: Re_кр =2320.

Швидкості, що відповідають критичним числам Рейнольда, також називають критичними. Наприклад, нижня критична швидкість - це швидкість, нижче якої настає ламінарний рух. Її можна визначити так: (2.14)

У всіх експериментальних визначеннях критичного значен­ня числа Re_Kp за перехідний режим від ламінарного до турбулент­ного беруть такий, який відповідає руйнуванню візуалізованих струменів рідини, тобто початку хаотичного перемішування рухо­мої маси рідини. Основні причини переходу ламінарного режиму у турбулентний такі:

1. Втрата стійкості ламінарного руху і наступний розвиток у струмені випадкових завихрувань.

2. Вплив кінцевих завихрувань, які утворює струмінь.

За ідеєю Тейлора, причиною турбулентності є вихори, що за­роджуються на нерівностях поверхні ( шорсткості ), по якій тече або яку обтікає струмінь.

Для інженерної практики дуже важливим є визначення втрат при різних режимах руху рідини.

4. Втрати напору

Рухома рідина на своєму шляху переборює сили тертя об стінки труби або каналу та різні місцеві опори , які трапляються на шляху потоку (крани , засувки, коліна, переходи, трійники то­що), внаслідок чого частка питомої енергії або напір втрачається.

Втрати напору враховуються четвертим членом рівняння Бернуллі. В усіх гідравлічних розрахунках водопровідно-ка­налізаційних систем необхідно враховувати такі втрати напору, тому що за цими втратами підбирають необхідний нагнітач (насос або компресор).

Втрати напору бувають двох видів: втрати напору вздовж потоку h_wl (втрати напору по довжині) і втрати напору на місце­вих опорах h_wm.

Сумарні втрати напору визначаються за формулою

(2.15)

де h_wl - сумарні втрати напору по довжині трубопроводу (русла і т. п.) на всіх його ділянках; h_wm - сумарні втрати напору на місце­вих опорах.

Втрати напору по довжині потоку зумовлені довжиною лінії подачі, шорсткістю стінок каналу (трубопроводу), в'язкістю ріди­ни, яка перекачується.

Втрати напору на місцевих опорах пов'язані з деформацією (зминанням) потоку, зміною характеру та напряму його руху. При цьому утворюються вихори, на формування яких і витра­чається частина енергії (напору).

Якщо відомі всі основні величини потоку (z, р, v), то втрати напору між двома перерізами можна визначити із рівняння Бер­нуллі (2.16)

(2.16)

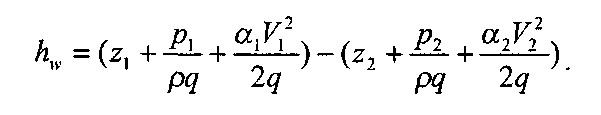
У системах водопостачання і водовідведення дуже важли­вим є визначення втрат напору в трубопроводах. Адже на загальні втрати напору в системі подачі вибираються необхідні насоси, компресори. Якщо в будь-якій системі подачі води втрати напору більші, ніж напір, який утворює відповідний насос, то така систе­ма працювати не буде.

Місцеві втрати напору виникають у місцях, де змінюється конфігурація потоку, яка призводить до деформації епюр роз­поділу швидкостей. На зміну конфігурації потоку витрачаєтьсядодаткова енергія. Відрізки потоку, в межах яких спостерігається зміна конфігурації, називаються місцевими опорами. Такими місцевими опорами є крани, клапани, коліна, різкі' звуження чи розширення труби або русла річок та ін.

Слід зазначити, що згаданії, вище втрати напору в цілому не втрачаються. Вони зумовлені переходом механічної енергії пото­ку в теплову. Щей ирощес є незворотним.

Механізмі дії сили опору дуже складний. Аналітично поки що не одержані точні теоретичні співвідношення до ш розрахун­ку. Для цього часто використовують емпіричні або напівемпіричні залежності.

Втрати напору по довжині будуть відмінними для різних видів руху потоку.

Визначення втрат напору при рівномірному рухові рідини у трубі

При ламінарному режимі у трубі постійного діаметра для визначення витрат і середньої швидкості руху рідини існують такі залежності:

Рис.12 – Схема до розрахунку втрат напору

У цих формулах Р₁ та Р₂ тиски відповідно на почат­ку і у кінці видаленого трубопроводу. Тоді визначаємо зміну тиску

(2.18)

Якщо у (2.18) замість динамічної в'язкості µ підста­вити кінематичну в'язкість v і густину ρ (µ=vρ),а потім розділити рівняння (2.18) нa pg , то одержимо

(2.19)

Ліва частина рівняння (2.19) представляє втрати напору на видаленій ділянці труби. Тоді рівняння (2.19) прийме вигляд

(2.20)

або, помноживши і поділивши на V, отримаємо:

Vd , (2.21)

де Re = — - число Рейнольдса.

v

Якщо помножити і поділити рівняння (2.21) на 2, то одер­жимо основне рівняння для визначення втрат напору по довжині трубопроводу (рівняння Дарсі - Вейсбаха)

(2.22)

де коефіцієнт гідравлічного тертя для ламінарного режиму руху потоку. Тобто втрати напору по довжині труби про­порційні її довжині, коефіцієнту гідравлічного тертя, а також швидкісному напорові за середньою швидкістю та обернено про­порційні діаметру труби.

Коефіцієнт λ - число абстрактне, значення якого вперше з'ясував Дарсі. Взагалі, рівняння Дарсі - Вейсбаха (2.22) є універ­сальним розрахунковим рівнянням, за допомогою якого можна визначити втрати напору по довжині труби як при ламінарному, так і при турбулентному режимах руху рідини. Структура форму­ли не змінюється, але коефіцієнт гідравлічного тертя для турбу­лентного режиму розраховуєтья залежно від ступеня розвитку турбулентності.

З цього приводу Нікурадзе в своїх дослідах виділив три ха­рактерні зони: зона гідравлічно гладких труб, перехідна зона і зо­на розвинутої турбулентності

Місцеві гідравлічні опори і втрати напору на них

Водоводи, нафтопроводи, канали тощо, по яких тече рідина, насичені різними поворотами, різними звуженнями чи розширен­нями, переходами, діафрагмами, засувками чи дисковими затво­рами і тому подібними елементами, які чинять додатковий опір руху рідини. На ділянках, де вони розташовані, втрачається час­тина енергії потоку. Оскільки довжина цих опорів незначна, то їх називають місцевими гідравлічними опорами.

Щодо природи втрат енергії потоку, то всі місцеві опори ма­ють одну загальну ознаку: на будь-якому місцевому опорі потік деформується. У результаті цього зростає градієнт швидкості, ут­ворюються вихори, а також відриви потоку від стінок, що викли­кає значні втрати напору в перерізі, де розташовано місцевий опір.

В інженерній практиці дотримуються такого правила: якщо довжина трубопроводу значна, а місцевих опорів відносно небага­то, то втрати напору на місцевих опорах не розраховують, а збільшують втрати напору по довжині на 8-10%.

Якщо трубопроводи порівняно короткі, а місцевих опорів багато (наприклад на збірному колекторі насосної станції), то обов'язково визначаються втрати напору на кожному місцевому опорі.

Втрати напору на такому місцевому опорі розраховуються за формулою:

(2.23)

де τ - коефіцієнт місцевого опору (вибирається залежно від виду місцевого опору); V- середня швидкість потоку переважно за цим опором.

Значення коефіцієнта місцевого опору вибирається залеж­но від його виду (кран, коліно, засувка чи інші)