23. Точные методы решения задач рнм

Движение жидкостей в пласте описываются диф- уравнениями в частных производных. Они выводятся из закона Дарси и уравнения неразрывности.В простейших случаях их решают аналитически, в более полной форме – с применением приближенных и численных методов.

Можно использовать методы:

1. функции комплексного переменного,

2. интегрального преобразования Лапласа,

3. автомодельного решения,

4. разделения переменных и др.

Задача 1. Плоское движение однородной несжимаемой жидкости в однородном недеформируемом бесконечном пласте с точечным источником описывается уравнением Лапласа ∂²p/∂²x+∂²p/∂²y=0 (1)

Введем потенциал фильтрации и ф-цию F(z)=Ф+iΨ (2) от комплексной переменной z=x+iy, (3) Ψ – функция линий тока.В курсе математ. физики доказывается, что F(z) можно представить в виде

(4)

отсюда (5)

Задача 2. Течение жидкости в неограниченном плоском пласте к бесконечной цепочке скважин

Достаточно рассмотреть одну полосу с одной скважиной и сформулировать задачу так: Определить дебит скважины по жидкости в полосообразной залежи шириной 2а.Плоскость (х,у) можно рассматривать как плоскость комплексной переменной z=x+iy и путем замены эту полосу можно преобразовать в неограниченную плоскость, для которой записывают решение аналогично (5). Затем переходят к исходным переменным и получают решение в виде

(6)

24. Метод эквивалентных фильтрационных сопротивлений

Метод эквивалентных фильтрационных сопротивлений — основной аналитический метод определения количественной связи между дебитами скважин и давлениями на их забоях и на контуре питания пласта (нагнетания воды) в условиях жесткого водонапорного режима. Сущность метода состоит в замене пол­ного фильтрационного сопротивления реального потока жидко­стей сложной конфигурации несколькими эквивалентными (равнозначными) последовательными или параллельными филь­трационными сопротивлениями простейших (прямолинейно-па­раллельных, плоскорадиальных) потоков. Понятно, что такая замена вносит определенную погрешность в результаты рас­чета, которая однако допустима при недостаточной точности исходной геолого-промысловой информации..

Рассмотрим простейший случай вытеснения нефти агентом, обладающим свойствами нефти (разноцветные жидкости), из однородного пласта по модели поршневого вытеснения (рис. 4.10).

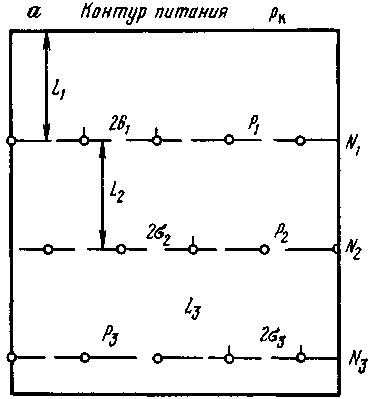
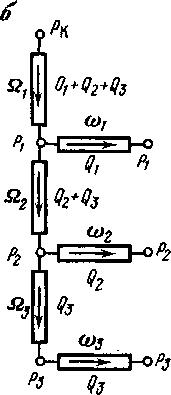
Рис. 4.10. Схема вытеснения нефти агентом:

а — расположение рядов скважин; б — эквивалентная электрическая схема рядов скважин

С помощью электрической схемы (рис. 4.10, б) построим систему уравнений для определения неизвестных дебитов рядов скважин. Если забой­ные давления во всех скважи­нах каждого ряда одинаковые, то Q₁ = n₁q₁, Q₂ = n₂q₂, Q₃ = n₃q₃

где Q_i — суммарный дебит i-го ряда скважин.

Из условия баланса закачки и отборов имеем

Q_н = Q₁ + Q₂ + Q₃

Перепад забойных давлений между:

нагнетательным и первым рядами добывающих скважин

p_н – p_с1 = Q_н(ω_н + Ω₁)+ Q₁ω₁

25. Проявление упругого режима. Основная формула упругого режима (по Щелкачеву в.Н.)

Разработка нефтяного месторождения при уп­ругом режиме  это осуществление процесса извлечения нефти из недр в усло­виях, когда Рпл превышает давление насыщения, поля давлений и скоростей продвижения нефти и воды, насыщающих пласт, а также воды в его законтурной области неустановившиеся, изменяющиеся во времени в каждой точке пласта.

С уменьшением пластового давления до значения, меньшего, чем давление насыщения, из нефти начнет выделяться растворенный в ней газ и режим пласта изменится  упругий режим сменится режимом растворенного газа или газонапорным.

Теорию упругого режима используют для решения следующих задач РНМ:

1.Определение параметров пласта по КВД. Суть методики: скважину эксплуатируют с постоянным дебитом, останавливают скважину, на забой спускают манометр, регистрируют изменение Рс до восстановления, по графику Рс=Рс(t) определяют гидропроводность и пьезопроводность пласта.

2. Гидропрослушивание. Суть метода:

-выбирают две скважины A и B. На забой скважины В спускают манометр;

-в скважине А изменяют режим ее работы,

-в скважине В регистрируют изменение ее дебита Δq и Рзаб.

- по кривой Рзаб.(t) определяют гидропроводность пласта между скважинами А и В.

3. Расчет изменения Р_пл на внешнем контуре нефтеносности или Р_ср по площади месторождения при разработке его в естественном режиме. Если нефтяное месторождение разрабатывается без воздействия на пласт и это месторождение окружено обширной водоносной областью с достаточно хорошей проницаемостью пород в этой области, то отбор нефти из месторождения и понижение пластового давления в нем вызовут интенсивный приток воды из законтурной в нефтеносную область разрабатываемого пласта.

4. При расчетах восстановления давления на контуре нефтеносного пласта в случае перехода на разработку месторождения с применением заводнения или при расчетах утечки воды в законтурную область пласта, если задано давление на контуре нефтеносности.

Если НМ в некот-й момент времени начинает разрабатываться с применением законтурного заводнения, то приток воды в нефтенасыщенную часть из законтурной области будет уменьш-ся, т.к. вытеснение нефти из пласта осущ-ется закачиваемой в пласт водой. С повышением давл-я на линии нагнетания приток воды в нефтенасыщенную часть месторождения из законтурной области сначала прекратится, а затем закачиваемая в пласт вода начнет утекать в законтурную область.

5. Расчет определения времени выхода на установившийся режим после пуска нагнетательной скв-ны.

Для того чтобы осуществлять расчеты процессов разработки нефтяных месторождений при упругом режиме, необходимо прежде всего получить дифференциальное уравнение этого режима, при выводе к-го исходят из уравнения не­разрывности массы фильтрующегося вещества:

За счет деформации твердого скелета пласта при изменении напряжения изменяется пористость пласта. β_с - коэффициент сжимаемости скелета пласта.

Пусть плотность жидкости линейно зависит от давления Р:

β_ж- коэффициент сжимаемости жидкости.

Закон Дарси (8)

При Р_r = const, учитывая (2)- (5), из (1) получим дифференциальное уравнение упругого режима.

где β=β_с+mβ_ж. χ и β – коэффициенты пьезопроводности и упругоемкости пласта.

Приближенные методы расчета давления при упругом режиме в замкнутой области:

Задача 1. Рассматривается радиальный приток жидкости к скважине с постоянным дебитом в неограниченном круговом пласте

При t=0 в области Р=Р_о

Законтурная водоносная область по размерам неограниченная. Отбор из скважин компенсиру­ется притоком воды из-за контура:

Решение, полученное Ван Эвердингеном и Херстом;

Функция φ(ρ,τ) записывается в виде интеграла от Бесселевых функций. При ρ=r/R=1 она ап­проксимируется формулой

Задача 2. Эта же задача при переменном дебите жидкости рассчитывается по интегралу Дюамеля.

Решение Щелкачева В.Н для случая работы скважины с постоянным дебитом в бесконечном круговом пласте: (12)

Еi- интегрально-показательная функция..

Формулу (12) Щелкачев назвал основной формулой теории упругого режима.

первым и вторым рядами добывающих скважин

p₁ – p₂ = – Q₁ω₁ +(Q₂ + Q₃)Ω₂+Ω₂ω₂

вторым и третьим рядами этих скважин

p₂ – p₃ = – Q₂ω₂ + Q₃(ω₃ + Ω₃)

Для любого ряда добывающих скважин

p_{i – 1} – p_i = Q_нω_н+ Ω₁ + Q_i ω_i – Q_{i – 1}ω_{i – 1} (4.30)

где i =1, 2, . . ., N, N — число рядов добываю­щих скважин.

Расчеты по формуле (4.30) показывают, что при одина­ковых забойных давлениях в рядах скважин суммарный дебит первых двух рядов со­ставляет более 90% от общего дебита. Это свиде­тельствует о высокой степени экранирующего влия­ния рядов при водонапорном режиме. В ре­альных условиях это влияние проявляется в зна­чительно меньшей степени.

По мере продвижения водонефтяного раздела период раз­работки залежи подразделяют на этапы — время продвижения фронта вытеснения от предыдущего ряда скважин до рассмат­ривае­мого. По теории поршневого вытеснения нефти из одно­родного пласта линия нагнетания перено­сится вслед за фрон­том вытеснения. В реальных условиях зонально-неоднородных и послойно-неоднородных пластов обводнение скважин про­ис­ходит по пропласткам неравномерно, что за­трудняет перенос фронта нагнетания.

Формулу для притока жидкости к скважине в полосообразной залежи запишем в виде

р_к–р_c=q [μL/(2аkh)+μln(а/(πr_c))/(2πkh)] (12)

Первое слагаемое характеризует фильтрацион­ное сопротивление при движение жидкости от контура до оси скважин (внешнее сопротивле­ние), второе- сопротивление при радиальном движении от кругового контура r_к=а/π до окруж­ности радиусом r_с

( внутреннее сопротивление)

Задача. Рассмотрим элемент однорядной системы с расстоянием между нагнетательной и до­бывающей скважинами L. Расстояние между скважинами в ряду 2а. Вытеснение поршневое, расстояние фронта заводнения от нагнетатель­ного ряда х_ф.

Запишем формулу для дебита по аналогии (12). В левой части должно быть 4 слагаемых:

• радиальное течение воды от контура r_с до r_к=а/π,

• прямолинейного течения воды от нагнета­тельного ряда до фронта воды,

• прямолинейного течения нефти от фронта до добывающего ряда,

• радиальное течение нефти от контура r_к=а/π до r_с

р_к –р_c=q/(2h) [μ_в ln(a/(π r_с))/ (π k_в)+ μ_в х_ф /(2 а k_в)+μ_н(L- х_ф)/(2аk_н)+ μ_н ln(а/(πr_c))/(πk_н)] (13).

Здесь L- расстояние от оси скважин до контура, Р_к – давление на контуре.

Задача 3.Приток жидкости с постоянным дебитом q к точечному стоку в однородном бесконечном пласте толщиной h при упругом режиме. Течение плоскорадиальное.

Задача описывается уравнением k/ μ (∂²p/∂r²+1/r(∂p/∂r))=β∂p/∂t (7)

Путем замены ξ=r/(æt)^1/2 уравнение (7) приводят к дифференциальному уравнению первого порядка, имеющем аналитическое решение. Затем возвращаются к исходным переменным и получают решение в виде

p_к-p=- qμ Ei[-r²/(4 æt) ] (8)

Это решение Щелкачев назвал основным уравнением упругого режима

Задача 4.Пусть имеется прямолинейный однородный пласт толщиной h, ограниченный двумя галериями. Начальное пластовое давление Р₀. Из левой галерии отбирают нефть с дебитом q, а на правой галерии х=l давление постоянно Р₀. Пласт разрабатывается в упругом режиме. Требуется определить распределение давления в пласте во времени.

Задача является одномерной и описывается уравнением (9)

Для решения можно использовать метод разделения переменных (метод Фурье) (10)

Уравнение (9) приводится к системе двух обыкновенных диф.уравнений: одно для φ, другое – для Ψ.

С учетом начальных и граничных условий, решение получим в виде (Р₁- значение давления при х=0, t→∞).

(11)