1.23 Проектирование боевых м-мов

Процесс прокладывания уточных нитей в зеве основы состоит из двух операций: прокладывания с большой скоростью уточной нити с одной стороны ткацкого станка на другую и закрепления по краям вырабатываемой ткани уточной нити, т. е. образова­ния кромок. В одних конструкциях эти операции выполняются одним и тем же механизмом, а в других они разделены и осу­ществляются отдельными, не зависящими друг от друга, механизмами.

Конструкции механизмов для прокладывания нити через зев разделяются на челночные и бесчелночные.

Челнок несет в себе уточную паковку. При бесчелночном же прокладывании уточная нить сматывается с неподвижно установленной бобины; в этом случае, как правило, требуется установка специальных кромочных устройств.

Челночные механизмы име­ют ряд положительных показателей:

1) могут перерабатывать любую пряжу; 2) могут работать на станках самой различной ширины; 3) качество тканей впол­не удовлетворительное; 4) кромки получаются без дополнитель­ных устройств.

Однако в связи с дальнейшим повышением производительности станков челночные боевые механизмы ограничивают скорость ткацких станков в силу большой массы и габаритов челнока с паковкой, а также из-за шума, производимого бое­выми механизмами.

К боевым механизмам предъявляют сле­дующие основные требования.

1. При правильном полете челнока с одной стороны станка на другую он должен лететь вдоль бруса и, таким образом, его относительная траектория должна быть прямой линией. Для соблюдения этого условия необходимо чтобы:

1) в челночной коробке в процессе разгона челнок двигался прямолинейно под действием ведущего прямолинейно-направ­ляющего механизма и 2) в зеве во время свободного полета челнок под действием сил инерции прижимался к берду для сохранения направления.

2. Разгон челнока в челночной коробке должен протекать по известному закону. Процесс боя должен проходить так, чтобы скорость челнока от нуля до максималь­ного значения изменялась плавно, без скачков.

3. Скорость вылета челнока в зев должна быть строго определенной: с одной стороны, она должна быть достаточной для быстрого пролета из одной челночной коробки в другую. С другой стороны, при высоких скоростях динамические сопротивления возрастают пропорционально квадрату скорости.

4. Процесс влета челнока в зев должен быть строго увязан с процессом открытия зева, с одной стороны, и положением батана — с другой. Движение челнока через зев должно быть согласовано с движениями батана и ремизок.

5. Положение челнока после влета в челночную коробку должно быть строго фиксировано. Это особенно важно при автоматическом ткачестве.

6. Тормозное устройство в челночных коробках должно предохранить гонок от быстрого разрушения челноком. С другой стороны, сам челнок не должен обгорать от нагревания, вызы­ваемого сильным трением.

7. При проектировании боевого механизма необходимо предусматривать возможность регулирования размеров звеньев для изменения силы боя.

8. Необходимо, чтобы материал челнока отличался легко­стью, прочностью и хорошо сопротивлялся износу от трения.

9. Боевой механизм должен быть прочен, прост по конструк­ции, удобен для обслуживания и безопасен для рабочих.

10. С одновременным обеспечением прочности звеньев боевого механизма не следует увеличивать вес и моменты инерции их масс.

11. Боевой механизм должен быть эластичным, легко вос­принимать упругий заряд в начале боя и отдавать энергию в конце боя.

После установления требований, предъявляемых к работе боевого механизма, конструктор может переходить к выбору кинематической схемы механизма и к определению кинемати­ческих размеров и взаимного расположения звеньев.

Боевые механизмы, в зависимости от расположения деталей их в станке, можно разделить на три основные группы:

1) верхнего боя; 2) нижнего боя; 3) среднего боя.

С другой стороны, боевые механизмы классифицируются по способу передачи движения погонялке.

В этом отношении боевые механизмы также подразделяются на три группы:

1) кулачковые; 2) кривошипные; 3) пружинные.

Проектирование боевого механизма нижнего боя

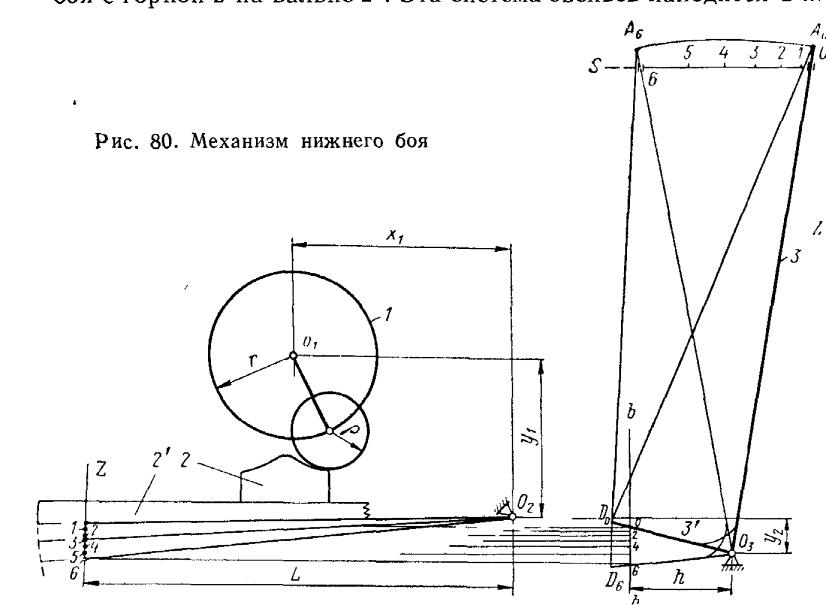
Проектирование механизма нижнего боя

В боевой шайбе 1 проступного вала (рис. 80) при радиусе r закреплена ось каточка радиуса , контактирующего в фазе боя с горкой 2 на вальке 2'. Эта система звеньев находится в плоскости поперечного разреза станка. Конец валька в перпендикулярной плоскости ZZ контактирует с отростком 3' башмака погонялки 3 с осью вращения О₃, установленной на подбатанном вале. Погонялка совершает переносное движение вместе с батаном и относительное вращательное движение в плоскости батана.

Разметка путей звеньев боевого механизма производится следующим образом. Вычерчивается кинематическая схема механизма с базисными размерами х₁, у₁ и y₂, определяющими взаиморасположение неподвижных осей. Затем выбираются кинематические размеры кривошипа r, радиус каточка , длины валька L, плеча отростка погонялки h и длины погонялки R = O₃A, на которой установлен гонок, движущийся по линии склиза SS и одновременно перемещающийся вдоль погонялки. От начального положения гонка O производим по линии склиза батана разметку путей челнока согласно ранее полученному графику путей Y_S (см. рис. 79, в).

Рассматривая погонялку с ее отростком в виде жесткого треугольника О₃AD (рис. 80), строим для размеченных точек ряд последовательных положений этого звена так, что каждый раз плечо погонялки O₃A занимает последовательные положения 0 - 6 на линии SS движения гонка. Отмечаем точки пересечения линии O₃D отростка погонялки со следом bb плоскости движения валька и переносим эти точки в левую проекцию на след ZZ плоскости движения погонялки. Перенесенные таким образом точки определяют последовательные положения валька 2' или разметку его положений.

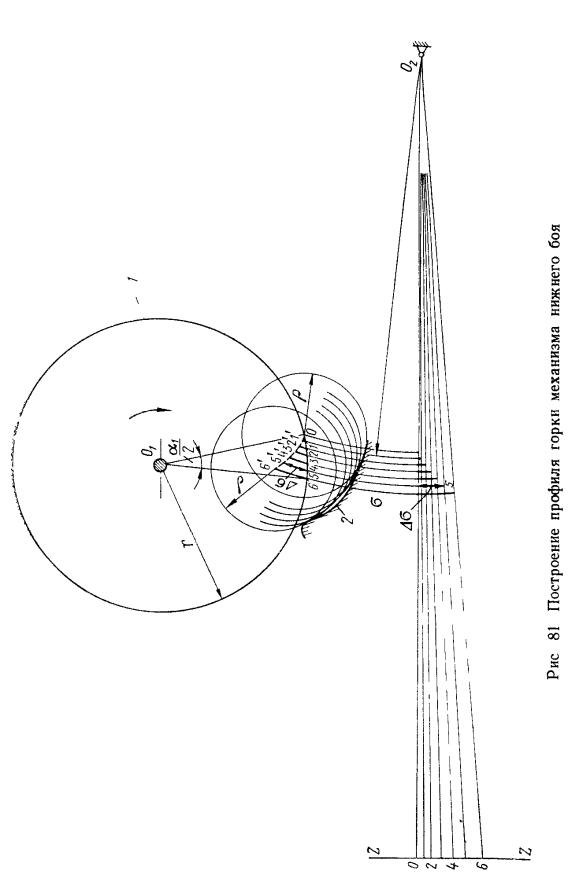
Для построения профиля горки 2 (рис. 81) воспроизводим на чертеже указанные промежуточные положения валька и фиксируем положения каточка боевой шайбы в начальный момент боя (положение О). От этого начального положения отложим в направ- лении вращения боевой шайбы угол боя по проступному валу и разделим дугу окружности радиуса r на равное число делений в соответствии с числом выбранных промежуточных положений механизма. Через эти точки делений проводим дуги  с центром в O₂, пересекающие линии положений валька. Отмечаем по каждой дуге длину приращений дуг  между линией начального положения валька и его последующими положениями. Переносим  по дуге  от точек 0 - 6 внутрь окружности шайбы. Ко-нечные точки 0 - 6' отложенных таким образом дуг принадлежат теоретическому профилю горки. Описывая вокруг этих точек окружности радиуса каточка  и построив плавную огибающую к окружностям, получим практический профиль горки.

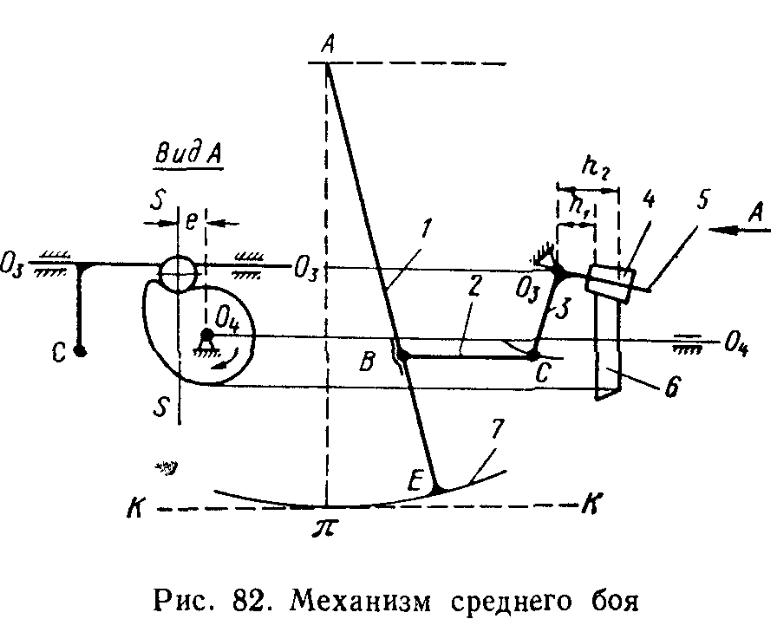
Проектирование боевого механизма среднего боя

В механизме среднего боя обеспечивается прямолинейное движение закрепленного на конце погонялки гонка. Наиболее широкое применение в автоматических ткацких станках имеют механизмы с погонялкой 1 (рис. 82), которая в кинематическом отношении представляет собой спицу колеса, перекатывающегося частью своего обода (башмак 7) по плоскости кронштейна KK подбатанного вала. Погонялка вмонтирована в челночную коробку батана и вместе с ним совершает переносное движение. Хомутом 2 она сочленена со стременем 3 веретена, вращающимся относительно оси О₃ и несущим каточек 4, контактирующий с боевым кулачком 6, установленном на проступном вале О₄. Как видно из боковой проекции слева, ось шпинделя каточка 5 движется в плоскости SS. Эта плоскость смещена относительно оси О₄ на расстояние e, называемое эксцентриситетом кулачка 6.

Полагая, что погонялка в своем движении относительно батана при перекатывании по кронштейну KK движется без скольжения, все ее остальные точки описывают циклоидальные траектории: точки на окружности башмака — обычные циклоиды, точки на радиусе спицы АЕ — укороченные циклоиды (вне радиуса —удлиненные циклоиды).

Рассмотрим способ построения укороченной циклоиды для точки В (рис. 83) сочленения погонялки с хомутом. Допустим, что погонялка радиуса A₀E₀ занимает начальное положение на горизонтальной прямолинейной направляющей КК. Дуга ₀ баш-

мака погонялки касается этой направляющей в точке ₀ —мгновенном центре вращения или полюсе скоростей.

Если задано любое другое положение точки А (обозначено соответствующими индексом 0—6), например, А₁ конца погонялки, то аналогичным образом находим соответствующий мгновенный центр вращения ₁ и дугу башмака ₁ радиуса A₁E₁. Определим на дуге ₁ ту точку ₁, которая в условиях перекатывания без скольжения совпадает с мгновенным центром ₁ при положении погонялки A₁E₁. Длина перекатывания ₀₁ должна быть равна длине дуги перекатывания по башмаку, т. е. ₀₁=₀₁’. Определив таким образом точку ₁’ на дуге ₀, находим длину дуги ₁’E₀ до основания погонялки Е и отложим ее по дуге ₁ от мгновенного центра ₁.

Определяем новое положение основания Е погонялки на дуге ₁. Соединив эту точку с концом погонялки, получим новое положение погонялки, на котором откладываем неизменное расстояние B₀E₀ и определяем положение точки В₁. Ряд последовательных построений точек В представляет собой геометрическое место укороченной циклоиды.

При вертикальном положении погонялки А₃E₃ циклоида имеет наинизшую точку. Мгновенный центр вращения ₃ cовпадает с точкой E₃. В последующих положениях основание Е погонялки располагается по левой части дуг башмака .

На линии пути aa гонка А (рис.84) производим разметку путей для четырех промежуточных положений механизма A₀ – A₃ точки А и строим соответствующие положения точки В на укороченной циклоиде. Из точек B₀ – B₃ и т. д. засекаем неизменной длиной хомута ВС дуговую траекторию _c шарнирного сочленения С хомута со стременем. Кинематическая длина стремени СО₃ и ось шпинделя каточка О₃S взаимно перпендикулярны и образуют прямой угол.

Таким образом, выполняем разметку положений оси О₃S шпинделя каточка и точки 0, 1, 2, 3 и т.д. пересечения этих осей плоскостями I—I и II—II, принадлежащими боковым граням кулачка.

Если кинематическая схема боевого механизма выполнена в уменьшенном масштабе, то для построения точек пересечения осей OS с кулачковыми плоскостями в натуральном масштабе достаточно увеличить соответствующее расстояние h₁ и h₂ до натурального размера h_H. Так как разметка точек S₀ – S₃ используется в дальнейшем для построения профилей боевого кулачка, то положение точек рекомендуется зафиксировать ординатами

y₀ – y₃ относительно горизонтальной оси O₃X.

Расчёт деталей боевого механизма на прочность

Основным фактором, определяющим силовую нагрузку боевого механизма, является инерционное сопротивление звеньев. Силы инерции отдельных звеньев распределяются внутри звена соразмерно элементарным точечным массам и их ускорениям. Рассмотрим хомут боевого механизма (рис. 87) с равномерно распределенной вдоль его длины l массой m, совершающий ускоренное поступательное движение в направлении своей длины и нагруженный силой сопротивления P₀. Для ускоренного движения тела необходимо наличие на ведущем его конце силы

,

где - ускорение тела.

Расчет такого тела на прочность следует вести по наибольшей силе P_K, а деформация удлинения l определяется по среднему усилию

или

.

Рассмотрим веретено боевого механизма с массами m_D шпинделя с каточком, m₀ вала веретена и m_C стремени (рис.88). Веретено догружено силой сопротивления P_C и вращается ускоренно под действием силы

,

где _B – угловое ускорение;

J_B – момент инерции массы веретена;

h₁ и h₃ – плечи.

Если необходимо определить прогиб конца стремени f_C точки С, то при расчете следует принять во внимание силу Р₀ и инерционные сопротивления массы стремени соразмерно распределению масс вдоль стремени и ускорениям W его точек.

При определении деформации скручивания вала веретена в расчет принимается, помимо силы Р₀, вся масса стремени m_C и часть (половина) массы вала m₀.

Лишь при расчете деформации изгиба шпинделя каточка надо учитывать как силу Р₀, массы m_C и m₀, так и всю массу шпинделя с каточком.

Приведенную к концу D стремени деформацию определяем с учетом силы Р₀ и половины момента инерции массы веретена при приведенном значении податливости

,

где е₁— податливость точки С при изгибе стремени в см/кг;

е₂ — угловая податливость вала веретена в 1/кГ*см;

e₃ — податливость при изгибе шпинделя каточка в точке D в см/кг.

В основу нашего последующего анализа положим схему нагрузки боевого механизма замещающими массами, показанную на рис. 89. Замещающая масса челнока и гонка m₁ сосредоточена в точке A, а замещающая масса погонялки m₂ —в точке В. Масса хомута m₃ разделена пополам и сосредоточена cоответственно в точках В и С. Дополнительно в точке С сосредоточена половина замещающей массы веретена m₄. Податливость звеньев механизма на участках между точками положения замещающих масс обозначены соответствующими индексами этих масс.

Рассматриваемый контур (как колебательная система) имеет четыре степени подвижности (свободы). Но в этом контуре основную роль играют колебания погонялки при ее относительно высокой податливости. Собственные колебания хомута и веретена при их меньшей податливости имеют малую амплитуду и более высокую частоту. Кратковременный процесс заряда боевого механизма происходит в одноименных фазах колебаний отдельных масс.

Таким образом, отношения путей, скоростей и ускорений точек B и С приложения масс m₂, m₃ и m₄ к пути, скорости и ускорению точки А является постоянными, равными . При этом колебательный контур имеет одну степень подвижности. Исходя из такой позиции построена и теория проф. А. П. Малышева по боевым механизмам.

Стрела прогиба f₁ конца А погонялки (рис. 90, а) под действием сопротивления челнока составляет (без влияния легкой массы конца погонялки)

,

где —фактическое ускорение челнока.

Рассматривая равновесие погонялки и пренебрегая поступательной частью ее движения, определяем из уравнения моментов относительно мгновенного центра  вращения движущее усилие Р_B со стороны хомута ВС

.

Из равновесия хомута ВС (рис. 90, б)

.

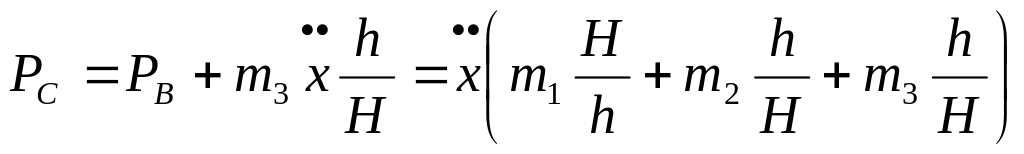Среднее значение силы, действующей на хомут

.

По силе Р_BC находив удлинение хомута

и приведенную к точке А деформацию от хомута

.

Деформацию веретена l_C в точке С определяем по приведенной податливости e_3-4 и усилию

.

Относя эту деформацию к точке А, получим

.

Суммируя прогибы и группируя слагаемые с одноименными массами, имеем:

.

Как видно из у равнения, каждый член этого выражения представляет собой произведение силы инерции замещающей массы звена, условно помещенной в точке А погонялки, на податливость части ведущего контура, заключенного между фактическим положением данной массы и ведущей точкой D.

Если помимо инерционных сил учитывается сила R сопротивления трения челнока, то приведенная к точке А деформация определяется аналогично деформации от :

.

Деформация f₅ от действия силы пружины Р_ПР, прикрепленной к погонялке (см. рис. 89) без начальной ее затяжки, определится

или

где С_n — жесткость пружины;

x — перемещение точки А.

Деформация пружины равна

.

Деформация от силы натяжения пружины на веретене очень мала и ею пренебрегаем.

Таким образом, можно представить приведенную к концу погонялки A деформацию , как сумму

Суммарная приведенная деформация представляет собой разность между номинальным путем s движения конца погонялки и фактическим x в динамических условиях (рис. 91).

,

где s —номинальный (кинематический) путь точки А;

x—фактический путь.

Тангенсы углов и наклона касательных к кривым s и x дадут мгновенное значение номинальных и фактических скоростей движения в процессе его разгона.