3. Методические указания к расчету индекса рентабельности инвестиций

Индекс рентабельности инвестиций, который еще называют индексом прибыльности, относится к классу относительных, показателей эффективности инвестиционного проекта. Он рассчитывается как частное от деления суммы приведенных будущих поступлений на приведенную стоимость затрат.

t_k

_ΣP(t)α(t)

t=1

P I= (4.3)

t_k

_ΣЗ(t)α(t)

t=0

Используя для выбора лучшего инвестиционного проекта индекс прибыльности, следует помнить, что его значение для эффективных проектов больше единицы.

4. Методические указания к расчету внутренней нормы прибыли

Под внутренней нормой прибыли понимают значение ставки дисконтирования

(р), при которой чистый приведенный доход от проекта (NРV) равен нулю.

IRR = р, при этом NРV = 0.

Если проект финансируется за счет кредита коммерческого банка, то значение IRR показывает максимальную величину банковской, процентной ставки, которая может быть покрыта за счет чистых доходов от проекта.

Данный показатель может быть рассчитан приближенно графическим методом и точно путем определения корней многочлена, коэффициентами которого являются значения чистого приведенного дохода по годам расчетного периода. Рассмотрим эти два метода.

Формула для расчета NРV может быть записана следующим образом:

_t=tk

NРV=_Σ[P(t)-З(t)]·(1+p)^-t (4.4)

^t=0

Изменяя величину ставки дисконтирования р, можно найти её значение, при котором NРV станет равным нулю. Это и будет величиной IRR, что показано на рис. . 4.2.

N PV

IRR

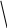
25 50 75 P%

Рис 4.2

Для более точного определения IRR составим следующий многочлен. .Пусть расчетный период Т = 5 годам, а шаг расчета t равен одному году и принимает последовательно значения 0, 1,2, 3, 4, 5. Зная, что IRR = р при NРV = 0, составим следующее уравнение.

NРV = [Р(0) - З(0)]·(1+p) ^-0 +[Р(1) - З(1)]·(1+p)^-1+ [P(2)-З(2)]·(1+p)^-2 +[P(3) - З(3)]·(1+р)^-3 +[Р(4) – З(4)]·(1+р)^-4+[Р(5) – З(5)]·(1+р)^-5

Далее запишем это уравнение в виде многочлена а_о + а_1х + ... + а_n-1x^n-1 + а_nхⁿ = 0

1

Г де х= _1+p (4.5)

Найдем корки этого многочлена. Среди них наименьший положительный. Подставив его значение в (4.5) и учитывая, что при этом р = 1КК, найдем значение внутренней нормы прибыли.

5. Методические указания к расчету дисконтированного периода окупаемости проекта

Дисконтированным периодом окупаемости проекта называется время, за которое сумма дисконтированных денежных поступлений от реализации проекта покроет сумму дисконтированных затрат. Период окупаемости обычно измеряется в годах или месяцах.

Его можно определить графическим методом, для чего необходимо построить зависимость чистого приведенного дохода от величины расчетного периода (Т). Точка пересечения этого графика от времени дает значение периода окупаемости проекта (DРР), что показано на рис. 4.3.

N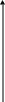 PV

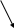
1 2 3 4 5 Т[в годах]

Рис. 4.3

Таблица 4.1

Первый инвестиционный проект

№ шага расчета	Ставка дисконти­рования %	Оценки элементов денежного потока в рублях *1000, выбираются в соответствии с предпоследней цифрой зачетной книжки
		0	1	2		3		4		5		6		7		8		9
		ПРИТОК денежных средств
0	-	-	-	-	-		-		—		—		-		—		—
1	23	300	320	330	340		360		370		380		390		400		410
2	23	320	360	380	360		370		380		390		405		-450		520
3	23	350	360	380	390		380		390		420		470		480		540
4	23	410	360	380	400		390		420		450		430		510		560
5	23	420	370	380	400		410		165		490		445		540		570
		ОТТОК денежных средств
0	-	С	С	С	С		С		С		С		С		С		С
1	23	180	190	190	200		200		240		240		250		250		288
2	23	180	190	195	220		200		240		240		250		250		295
3	23	190	200	210	220		200		244		242		255		260		300
4	23	190	200	210	220		210		248		244		255		260		300
5	23	190	200	210	225		210		250		245		255		260		300

где С инвестиционные затраты на проект, сделанные до начала эксплуатации проекта.

С = последняя цифра зачетной книжки *1000+1000

Таблица 2 Второй инвестиционный проект

Номер шага расчета	Ставка дисконти­рования %	Оценки элементов денежного потока в рублях *1000, выбираются в соответствии с предпоследней цифрой зачетной книжки
		0	1	2		3		4		5		6		7		8		9
		ПРИТОК денежных средств
0	-	-	-	-	-		-		—		—		-		—		—
1	23	334	345	353	400		440		445		490		530		590		650
2	23	405	360	360	440		460.		470		500		540		610		440
3	23	450	360	400	430		480		480		520		550		600		460
4	23	540	370	450	400		480		М490		520		550		630		450
5	23	540	520	500	490		470 '		1510		530		560		600		480
		ОТТОК денежных средств
0	-	С	С	С	С		С		С		С		С		С		С
1	23	210	220	225	230		235		240		245		250		255		260
2	23	215	220	225	230		235		240		245		250		255		275
3	23	220	220	230	235		245		240		255		260		270		280
4	23	225	225	230	240		245		250		255		260		270		285
5	23	230	225	230	240		245		250		255		260		270		285

где С инвестиционные затраты на проект, сделанные до начала эксплуатации проекта.

С = последняя цифра зачетной книжки *1000+1000

ЗАДАЧА. Имеются пять объектов для инвестиций: А, В, С, О и Е. Для каждого объекта известна его прибыльность (в процентах от вложенной суммы), надежность (измеряется в баллах от 1 до 10) и оценка срока функционирования объекта после инвестиции-. Требуется распределить некоторую сумму инвестиций между этими объектами с учетом следующих ограничений:

• общая сумма инвестиций не должна превышать заданное значение 5;

• инвестиция в один объект не может быть больше 25% от общей суммы 3;

• общая сумма инвестиций в объекты с надежностью менее 6 баллов не должна превышать 33% от общей суммы 5;

• не менее 40% всех средств должны быть вложены в объекты со сроком функционирования более 5 лет.

Бакалавр должен методом подбора (методом проб и ошибок) найти решение по распределению инвестиций, удовлетворяющее заданным ограничениям, и рассчитать общую прибыль для каждого решения. Общая прибыль рассчитывается путем умножения прибыльности каждого объекта, выраженной в долях единицы, на сумму инвестиции в тот объект и последующего суммирования по всем объектам..

Примечание. решения, которые бакалавр представит в контрольной работе, должны достаточно заметно отличаться друг от друга по величине инвестиций (по крайней мере для одного из объектов это отличие должно составлять не менее 5-10%).

Вариант исходных данных задачи выбирается в соответствии с цифрами зачетной книжки и годом ее выполнения

ВАРИАНТЫ КР

Прибыль Проекта (тыс руб.)	последняя цифра зачетной книжки
	1	2	3	4	5	6	7	8	9	0
А	30	34	7	53	61	41	49	85	8	8
В	80	1	79	89	90	67	48	1	47	74
С	78	52	14	39	26	70	48	45	69	4
D	8	80	16	85	98	37	54	94	88	95
Е	23	78	39	37	14	53	28	4	54	27

Риск Проекта (баллов)	последняя цифра зачетной книжки
	1	2	3	4	5	6	7	8	9	0
А	18	18	17	20	40	4	3	17	13	35
В	29	13	15	10	32	21	0	16	20	17
С	31	20	28	4	24	6	27	3	14	30
D	6	32	29	27	6	6	36	0	21	24
Е	19	38	31	3	33	13	31	21	36	32

Срок Проекта (лет)	Год выполнения КР
	2006	2007	2008	2009	2010	2011	2012	2013	2014	2015
А	2	11	3	11	4	2	9	4	12	2
В	9	11	1	2	4	9	2	2	11	6
С	12	3	12	8	2	6	5	2	2	10
D	1	8	9	3	9	4	6	1	11	5
Е	7	7	5	1	6	9	12	7	11	7

Задание.

1. Найти 4 сочетания значений инвестиций, удовлетворяющие заданным ограничениям

2. Найти сочетание инвестиций, обеспечивающее максимум прибыли

3. Найти сочетание инвестиций, обеспечивающее минимум финансового риска

Пример выполнения и оформления задачи

ЗАДАЧА. Имеются пять объектов для инвестиций: A, B, C, D и E. Максимальная общая сумма инвестиций составляет 700тыс.долл. Прибыльность каждого объекта (в процентах от вложенной суммы), надежность (оценивается в баллах от 1 до 10) и оценка срока функционирования объекта после инвестиции приведены ниже:

Объект	A	B	C	D	E
Прибыльность %	11	12	16	40	11
Надежность, баллы (R)	9	8	4	5	9
Срок функц., лет	3	7	12	4	2

Требуется распределить инвестиции между этими объектами с учетом следующих ограничений:

• общая сумма инвестиций не должна превышать заданное значение 5;

• инвестиция в один объект не может быть больше 25% от общей суммы 3;

• общая сумма инвестиций в объекты с надежностью менее 6 баллов не должна превышать 33% от общей суммы 5;

• не менее 40% всех средств должны быть вложены в объекты со сроком функционирования более 5 лет.

Требуется найти два решения по распределению инвестиций, удовлетворяющих заданным ограничениям, рассчитать общую прибыль для каждого решения и указать более выгодное решение.

Введем обозначения:

SА - инвестиция в объект А,

SВ - инвестиция в объект В,

SС - инвестиция в объект С,

SD - инвестиция в объект D,

DЕ - инвестиция в объект Е.

Запишем ограничения с учетом указанных обозначений.

1) Ограничение на общую сумму инвестиций:

SА+SВ+SС+SD+SЕ <= 700.

2) Ограничения на размер инвестиции в один объект:

SА<=0,25*700; SВ<=0,25*700; SС<=0,25*700; SD<=0,25*700; SЕ<=0,25*700.

3) Ограничение на общую сумму инвестиций в объекты с надежностью менее 6 баллов:

SС+SD<= 0,33*700.

4) Ограничение на общую сумму инвестиций в объекты со сроком функционирования более 5 лет:

SВ+ SC=0,40*700.

5) Естественные дополнительные ограничения на неотрицательность

инвестиций:

SА >= 0; SВ >= 0; SС >= 0; SD>= 0; SЕ >= 0.

RA·SA+SB·RB+SC·RC+SD·RD+SE·RE

6 ) R= ,

100

где, RA – риск (надежность) инвестиций в объекте А.

Найдены следующие два решения задачи, удовлетворяющие заданным ограничениям.

РЕШЕНИЕ 1.

Объекты	А	В	С	D	Е
Инвестиции	140	160	120	110	170

Выполнение ограничений:

1) SA+SB +SC +SD +SE =700

Ограничение SA+SB +SC +SD +SE <= 700 выполнено.

2) 0,25*700=175.

Ограничения SА<=175, SВ<=175, SС<=175, SD<=175, SЕ<=175

выполнены.

3) 0,33*700=231; SС+SD=120+110=230.

Ограничение SС+SD<=231 выполнено.

4) 0,40*700=280; SВ+SC=160+120=280

Ограничение SВ+ SC>=280 выполнено .

5) Ограничения SА >=0, SВ >=0, SС >=0, SD >= 0, SЕ >= 0 выполнены

Общая прибыль:

0,11 * 140+0,12* 160+0,16* 120+0,40* 110+0.11 * 170=116,5.