15. Дифференциальное уравнение вынужденных колебаний и его решение

. Решение уравнения: общее решение однородного уравнения: , + частное решение: .

16. Понятие о резонансе

Резонанс – явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы (частоты вынуждающего переменного напряжения) к частоте, равной или близкой собственной частоте колебательной системы. резонансная частота - частота, при которой амплитуда А смещения (заряда) достигает максимума. рез= . Арез=х0/(2 )

17. Сложение гармонических колебаний одного направления. Метод векторных диаграмм.

Колеблющееся тело может участвовать в нескольких колебательных процессах, тогда необходимо найти результирующее колебание, иными словами, колебания необходимо сложить. Сложим гармонические колебания одного направления и одинаковой частоты

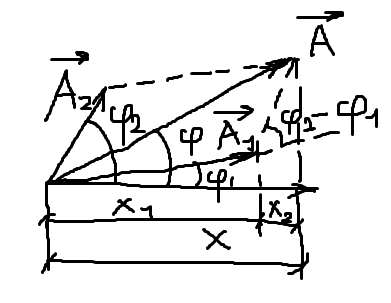. Используем метод векторных диаграмм. Т.к. векторы А1 и А2 вращаются с одинаковой угловой скоростью , то разность фаз

2-1 между ними остается постоянной. Уравнение

результирующего колебания: х=х1+х2=Аcos (t+), где

амплитуда А и фаза  задается соотношением:

.

С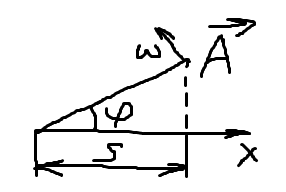 умма двух гармонических колебаний одного направления есть гармонические колебания в том же направлении и с той же частотой, что и у складываемых колебаний. Амплитуда результирующего колебания зависит от разности фаз складываемых колебаний. 1) 2-1=2mπ, где (m=0,1,2,…), тогда А=А1+А2. 2) 2-1=(2m+1)π, где (m=0,1,2,…), тогда А=|А1-А2|.

Метод векторных диаграмм: гармонические колебания изображаются

графически методом вращающегося вектора амплитуды или методом

векторных диаграмм. Из произвольной точки 0, выбранной на оси х, под

углом , равным начальной фазе колебаний, откладывают вектор А,

модуль которого равен амплитуде А рассматриваемого колебания. Если

вектор будет вращаться вокруг т. 0 с угловой скоростью , то проекция вектора на ось х будет совершать колебания по закону s=A*cos(t+)

18. Биения

Б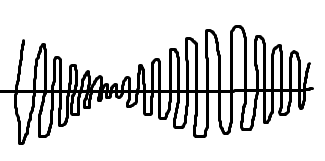 иениями называются периодические изменения амплитуды колебаний, возникающие при сложении 2-х гармоничных колебаний с близкими частотами.

Пусть амплитуды равны А, а частоты равны  и +, причем

<<,

х1=Аcost, х2=Аcos(+)t, результирующее колебание имеет вид

x=(2A cos(t/2))cost . – гармонические колебания с частотой , амплитуда которых изменяется по закону Абиения=| 2A cos(t/2)| с частотой = (частота биения вдвое больше частоты изменения cos, поскольку Абиения берем по модулю)

19. Сложение двух взаимно перпендикулярных гармонических колебаний.

Для простоты начало отсчета выберем так, чтобы начальная фаза первого колебания была равна нулю, и запишем , где α – разность фаз обоих колебаний; А и В – амплитуды складываемых колебаний. Уравнение траектории результирующего колебания находится исключением из выражения параметра t. После несложных преобразований получим уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно: . Так как траектория результирующего колебания имеет форму эллипса, то такое колебание называется эллиптически поляризованным.