Вероятности ошибок (уровень значимости и мощность)
Вероятность ошибки
первого рода при проверке статистических
гипотез
называют уровнем
значимости
и обычно обозначают греческой буквой
(отсюда
название
-errors).
Вероятность ошибки
второго рода не имеет какого-то особого
общепринятого названия, на письме
обозначается греческой буквой
(отсюда
-errors).
Однако с этой величиной тесно связана
другая, имеющая большое статистическое
значение — мощность
критерия. Она
вычисляется по формуле
.
Таким образом, чем выше мощность, тем
меньше вероятность совершить ошибку
второго рода.
Обе эти характеристики обычно вычисляются с помощью так называемой функции мощности критерия. В частности, вероятность ошибки первого рода есть функция мощности, вычисленная при нулевой гипотезе. Для критериев, основанных на выборке фиксированного объема, вероятность ошибки второго рода есть единица минус функция мощности, вычисленная в предположении, что распределение наблюдений соответствует альтернативной гипотезе. Для последовательных критериев это также верно, если критерий останавливается с вероятностью единица (при данном распределении из альтернативы).
В статистических тестах обычно приходится идти на компромисс между приемлемым уровнем ошибок первого и второго рода. Зачастую для принятия решения используется пороговое значение, которое может варьироваться с целью сделать тест более строгим или, наоборот, более мягким. Этим пороговым значением является уровень значимости, которым задаются при проверке статистических гипотез. Например, в случае металлодетектора повышение чувствительности прибора приведёт к увеличению риска ошибки первого рода (ложная тревога), а понижение чувствительности — к увеличению риска ошибки второго рода (пропуск запрещённого предмета).
16. Приведите формулу расчета коэффициента детерминации r2 и объясните его роль при определении качества построенного уравнения регрессии.
Коэффициент
детерминации
(
- R-квадрат)
— это доля дисперсии
зависимой переменной, объясняемая
рассматриваемой моделью
зависимости, то есть объясняющими
переменными. Более точно — это единица
минус доля необъяснённой дисперсии
(дисперсии случайной ошибки модели, или
условной по факторам дисперсии зависимой
переменной) в дисперсии зависимой
переменной. Его рассматривают как
универсальную меру связи одной случайной
величины от множества других. В частном
случае линейной зависимости
является
квадратом так называемого множественного
коэффициента
корреляции
между зависимой переменной и объясняющими
переменными. В частности, для модели
парной линейной регрессии коэффициент
детерминации равен квадрату обычного
коэффициента корреляции между y
и x.
Истинный коэффициент детерминации модели зависимости случайной величины y от факторов x определяется следующим образом:
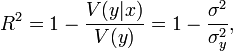
где
—
условная (по факторам x) дисперсия
зависимой переменной (дисперсия случайной
ошибки модели).
В данном определении используются истинные параметры, характеризующие распределение случайных величин. Если использовать выборочную оценку значений соответствующих дисперсий, то получим формулу для выборочного коэффициента детерминации (который обычно и подразумевается под коэффициентом детерминации):
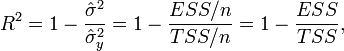
где
-сумма
квадратов остатков регрессии,
-
фактические и расчетные значения
объясняемой переменной.
-
общая сумма квадратов.
В случае линейной
регрессии
с константой
,
где
—
объяснённая сумма квадратов, поэтому
получаем более простое определение в
этом случае — коэффициент
детерминации — это доля объяснённой
суммы квадратов в общей:
Необходимо подчеркнуть, что эта формула справедлива только для модели с константой, в общем случае необходимо использовать предыдущую формулу.