Пример: простейшая (парная) регрессия

В случае парной линейной регрессии формулы расчета упрощаются (можно обойтись без матричной алгебры):

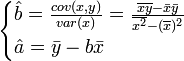
12. Сформулируйте условия Гаусса-Маркова в методе наименьших квадратов (мнк).

Теорема Гаусса-Маркова. При выполнении перечисленных пяти условий оценки неизвестных коэффициентов модели регрессии, полученные классическим методом наименьших квадратов, имеют наименьшую дисперсию в классе всех линейных несмещённых оценок.

Можно сделать вывод, что оценки коэффициентов модели регрессии, полученные классическим методом наименьших квадратов, являются оптимальными оценками, т.е. несмещенными, состоятельными и эффективными.

13. Что представляет собой нуль-гипотеза и в каких ситуациях она отвергается?

Нулевая гипотеза – это основное проверяемое предположение, которое обычно формулируется как отсутствие различий, отсутствие влияние фактора, отсутствие эффекта, равенство нулю значений выборочных характеристик и т.п. Примером нулевой гипотезы в педагогике является утверждение о том, что различие в результатах выполнения двумя группами учащихся одной и той же контрольной работы вызвано лишь случайными причинами.

Другое проверяемое предположение (не всегда строго противоположное или обратное первому) называется конкурирующей или альтернативной гипотезой. Так, для упомянутого выше примера гипотезы Н₀ в педагогике одна из возможных альтернатив Н₁ будет определена как: уровни выполнения работы в двух группах учащихся различны и это различие определяется влиянием неслучайных факторов, например, тех или других методов обучения.

Выдвинутая гипотеза может быть правильной или неправильной, поэ­тому возникает необходимость проверить ее. Так как проверку произво­дят статистическими методами, то данная проверка называется статистической.

При проверке статистических гипотез возможны ошибки (ошибочные суждения) двух видов:

— можно отвергнуть нулевую гипотезу, когда она на самом деле верна (так называемая ошибка первого рода);

— можно принять нулевую гипотезу, когда она на самом деле не верна (так называемая ошибка второго рода).

Ошибка, состоящая в принятии нулевой гипотезы, когда она ложна, качественно отличается от ошибки, состоящей в отвержении гипотезы, когда она истинна. Эта разница очень существенна вследствие того, что различна значимость этих ошибок. Проиллюстрируем вышесказанное на следующем примере.

14. В чём состоит ошибка (риск) 1 рода при тестировании гипотез?

Ошибки первого рода (англ. type I errors, α errors, false positives) и ошибки второго рода (англ. type II errors, β errors, false negatives) в математической статистике — это ключевые понятия задач проверки статистических гипотез. Тем не менее, данные понятия часто используются и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет) на основе некоего критерия (теста, проверки, измерения), который с некоторой вероятностью может давать ложный результат.

Пусть дана выборка из неизвестного совместного распределения , и поставлена бинарная задача проверки статистических гипотез:

где  — нулевая гипотеза, а  — альтернативная гипотеза. Предположим, что задан статистический критерий

,

сопоставляющий каждой реализации выборки одну из имеющихся гипотез. Тогда возможны следующие четыре ситуации:

1. Распределение выборки 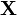соответствует гипотезе , и она точно определена статистическим критерием, то есть .

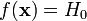2. Распределение выборки соответствует гипотезе , но она неверно отвергнута статистическим критерием, то есть .

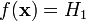3. Распределение выборки соответствует гипотезе , и она точно определена статистическим критерием, то есть .

4. Распределение выборки соответствует гипотезе , но она неверно отвергнута статистическим критерием, то есть .

Во втором и четвертом случае говорят, что произошла статистическая ошибка, и её называют ошибкой первого и второго рода соответственно.

		Верная гипотеза
Результат  применения  критерия		верно принята	неверно принята  (Ошибка второго рода)
		неверно отвергнута  (Ошибка первого рода)	верно отвергнута