39. Дайте определение гетероскедастичности наблюдений.

Гетероскедастичность - это явление неоднородности дисперсий случайных ошибок (остатков) модели регрессии (рис. 1).

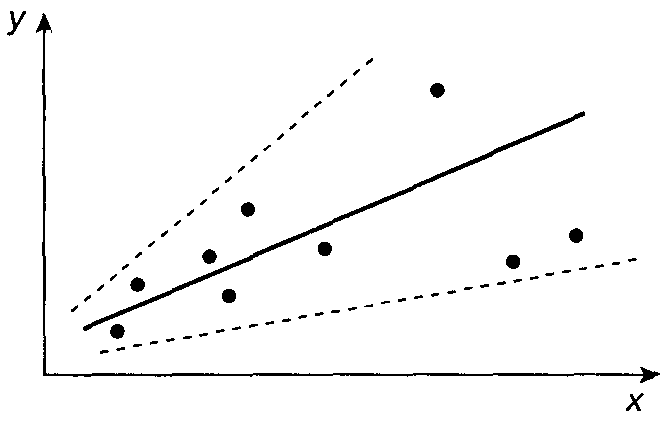
Рис. 1. Случай гетероскедастичности остатков

40. В чем заключается тестирование гетероскедастичности на основе теста Голдфелда – Квандта?

Предположим, что на основе проведённого исследования зависимость между переменными можно аппроксимировать линейной моделью множественной регрессии.

В модели множественной регрессии выбирается независимая переменная xik, от которой наиболее вероятно могут зависеть остатки модели ei.

На следующем этапе значения независимой переменной xik ранжируются

располагаются по возрастанию и делятся на равные 3 части.

Для I и III частей строятся две независимые модели регрессии вида:

Для каждой из построенных моделей регрессий рассчитываются суммы квадратов остатков:

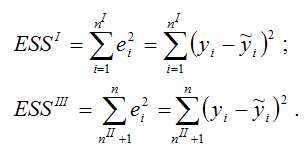
Основная гипотеза H0 предполагает постоянство дисперсий случайных ошибок модели регрессии, т. е. присутствие в модели условия гомоскедастичности:

Альтернативная гипотеза H1 предполагает непостоянство дисперсиий случайных ошибок в различных наблюдениях, т. е. присутствие в модели условия гетероскедастичности:

Данные гипотезы проверяются с помощью F-критерия Фишера-Снедекора.

Наблюдаемое значение F-критерия (вычисленное на основе выборочных данных) сравнивают с критическим значением F-критерия, которое определяется по таблице распределения Фишера-Снедекора.

Критическое значение F-критерия определяется по таблице распределения Фишера-Снедекора в зависимости от уровня значимости а и двух степеней свободы: k1=nI–l и k2=nI–l,  где l – число оцениваемых по данной выборке параметров.

Наблюдаемое значение F-критерия находят по формуле:

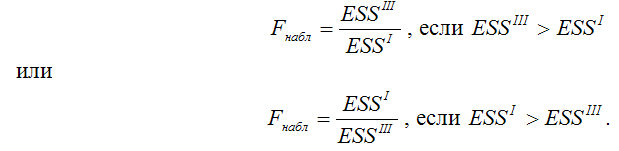
При проверке основной гипотезы возможны следующие ситуации.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) больше критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл›Fкрит, то основная гипотеза отвергается, и, следовательно, в модели регрессии присутствует гетероскедастичность, зависящая от переменной xik.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) меньше или равно критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл‹Fкрит, то основная гипотеза принимается, и гетероскедастичность в модели множественной регрессии не зависит от переменной xik.

На следующем этапе проверяются другие независимые переменные, если есть предположение об их тесной связи с G2(

Если тест Голдфелда-Квандта проводился для линейной модели парной регрессии, то вывод о принятии основной гипотезы означает гомоскедастичность построенной модели регрессии.

43. Сформулируйте теорему Айткена о коэффициентах обобщенного мнк.

МНК-оценки неизвестных коэффициентов модели регрессии, чьи случайные ошибки подвержены явлениям гетероскедастичности или автокорреляции, не будут удовлетворять теореме Гаусса-Маркова. Свойствами состоятельности и несмещённости МНК-оценки будут обладать, однако свойство эффективности в этом случае утрачивается.

Для вычисления оценок неизвестных коэффициентов модели регрессии с гетероскедастичными или коррелированными случайными ошибками используется обобщённый метод наименьших квадратов. Оценки, полученные с помощью данного метода, будут удовлетворять условиям состоятельности, несмещённости и эффективности.

В основе нормальной линейной модели регрессии среди прочих лежат условия о некоррелированности и гомоскедастичности случайных ошибок:

1) дисперсия случайной ошибки модели регрессии является величиной, постоянной для всех наблюдений:

2) случайные ошибки модели регрессии не коррелированны между собой, т. е. ковариация случайных ошибок любых двух разных наблюдений равна нулю:

Определение. Обобщённой линейной моделью регрессии называется модель, для которой нарушаются условия о гомоскедастичности и некоррелированности случайных ошибок.

Таким образом, обобщённая линейная модель регрессии характеризуется неоднородностью дисперсий случайных ошибок:

D(?i)? D(?j)?G2?const, где i?j,

и наличием автокорреляции случайных ошибок:

Cov(?i,?j)?E(?i,?j)?0 (i?j).

Матричный вид обобщённой линейной модели регрессии:

Y=X* ?+?,

где X – неслучайная матрица факторных переменных;

? – случайная ошибка модели регрессии с нулевым математическим ожиданием E(?)=0 и дисперсией G2(?):

?~N(0;G2?),

?  – ковариационная матрица случайных ошибок обобщённой модели регрессии.

Для нормальной линейной модели регрессии дисперсия случайной ошибки определялась на основе условия гомоскедастичности:

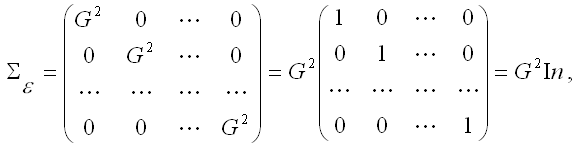
где G2=const – дисперсия случайной ошибки модели регрессии ?;

In – единичная матрица размерности n*n.

Для обобщённой модели регрессии ковариационная матрица случайных ошибок строится на основе условия непостоянства дисперсий остатков модели регрессии (гетероскедастичности) D(?i)? D(?j)?G2?const:

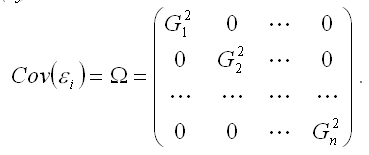
Отличие между нормальной линейной моделью регрессии и обобщенной линейной моделью регрессии заключается в матрице ковариаций случайных ошибок модели.

Теорема Айткена. В классе линейных несмещённых оценок неизвестных коэффициентов обобщённой модели регрессии оценка

будет иметь наименьшую ковариационную матрицу.

Общая формула для расчёта матрицы ковариаций ОМНК-оценок коэффициентов обобщенной модели регрессии имеет вид:

Величина G2(?)  оценивается по формуле:

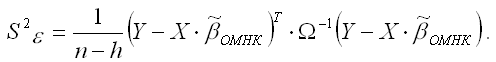
Однако значение G2(?)  не следует трактовать как дисперсию случайной ошибки модели регрессии.

Коэффициент детерминации не используется при оценке качества обобщённой линейной модели регрессии, потому что он не отвечает требованиям, предъявляемым к обычному множественному коэффициенту детерминации.

Проверка гипотез о значимости коэффициентов обобщенной линейной модели регрессии и модели регрессии в целом осуществляется с помощью тех же статистических критериев, что и в случае нормальной линейной модели регрессии.