
- •Кодеры систематического циклического кода: матричного типа и на регистрах сдвига с обратными связями: привести схемы и описать работу.
- •2 Строка
- •Кодеры несистематических циклических кодов: привести схемы и описать работу.
- •3. Низкоскоростные корреляционные коды: методы и схемы кодирования.
- •4. Низкоскоростные коды: методы и схемы корреляционного декодирования.
- •5.Коды бчх: схемы кодирования и алгоритмы декодирования.
- •7.Коды Рида-Маллера: схемы кодирования и алгоритмы декодирования.
- •8. Коды Хэмминга: схемы кодирования и алгоритмы декодирования.
- •9.Код Голея: параметры, доказательство оптимальности, схемы кодирования
- •10. Алгебро-геометрический подход
- •11.Алгоритм Берлекэмпа-Месси: его применение при декодировании помехоустойчивых кодов и при анализе линейной сложности криптографических функций
- •13.Линейные групповые коды: схемы кодирования и декодирования на основе модели смежных классов.
- •14.Минимальные многочлены и циклотомические классы, их связь с конечным полем, применение в теории кодирования.
- •15.Дуальные коды их свойства.
- •16.Методы вылавливания независимых и пачек ошибок.
- •17.Криптосистемы rsa: структура и принципы защиты информации.
- •18.Криптоанализ системы rsa.
- •19. Криптосистемы на эллиптических кривых (целые числа): структура и принципы защиты информации.
- •2 0.Криптосистемы на эллиптических кривых (расширенные поля Галуа): структура и принципы защиты информации.
- •21. Шифр aes: структура и принципы защиты информации
- •22.Криптографические протоколы метод доказательства с нулевым разглашением знаний.
- •23. Шифр Вернама и сеть Фейстеля.
- •Расшифрование
- •Алгоритмическое описание
- •24.Режимы включения криптомодулей блочных шифров
- •25.Протокол Фейге-Фиат-Шамира.
- •26. Оценка уровня нелинейности и линейной сложности криптографической функции
- •27. Линейный и дифференциальный криптоанализ
- •28.Понятие хеш-функций и их свойства.
- •29.Алгоритмы создания и проверки электронной цифровой подписи (эцп). Алгоритмы
- •Симметричная схема
- •Асимметричная схема
- •Виды асимметричных алгоритмов эп
- •30. Сверточные коды: схемы кодирования и алгоритмы декодирования.
- •1. Пороговое декодирование
- •Жесткое пороговое декодирование сск
- •1.2. Мягкое пороговое декодирование сск
- •2. Вероятностное декодирование сверточных кодов
- •2.1. Декодер Витерби
- •2.2. Последовательное вероятностное декодирование сверточных кодов
Кодеры систематического циклического кода: матричного типа и на регистрах сдвига с обратными связями: привести схемы и описать работу.
При
систематическом кодировании кодовое
слово формируется в виде
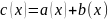
где

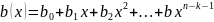
Для низкоскоростных кодов используют проверочный полином для кодирования
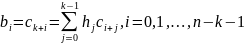
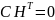

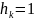
1
строка
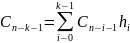
2 Строка
Кодер систематического кода по h(x)

Первые k тактов режим 1 – заполнения информационных символов. Следующие n-k тактов – режим работы 2. Схема формирует проверочные символы.
Кодирование
с помощью циклического кода в
систематической
форме включает в себя вычисление битов
четности, как результат деления
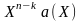 по
модулю g(X),
т.е., деление
смещенного
вправо (смещенного вверх) многочлена
сообщения на порождающий многочлен
g(X).
Сдвиг вправо приводит к освобождению
места для битов четности, которые
прибавляются к разрядам сообщения, что
в результате дает вектор кода в
систематической
форме. На n
– k
разрядов сообщения сдвиг вправо
является тривиальной операцией
и в действительности не выполняется в
схеме деления. На самом деле вычисляются
только биты четности, затем они помещаются
на соответствующие места
рядом с битами сообщения. Многочлен
четности –
это остаток от деления на порождающий
многочлен g(X).
Он находится в регистре после п
сдвигов
через (n
– k)
–
разрядный
регистр сдвига с обратной связью.
Заметим, что
первые n
– k
сдвигов по разрядам –
это просто заполнение регистра. Однако
никакой
обратной связи не будет, пока не будет
заполнен крайний справа разряд.
Следовательно, надо сократить цикл
деления, загружая входные данные
с выхода последнего разряда, как показано
на рисунке 1.
по
модулю g(X),
т.е., деление
смещенного
вправо (смещенного вверх) многочлена
сообщения на порождающий многочлен
g(X).
Сдвиг вправо приводит к освобождению
места для битов четности, которые
прибавляются к разрядам сообщения, что
в результате дает вектор кода в
систематической
форме. На n
– k
разрядов сообщения сдвиг вправо
является тривиальной операцией
и в действительности не выполняется в
схеме деления. На самом деле вычисляются
только биты четности, затем они помещаются
на соответствующие места
рядом с битами сообщения. Многочлен
четности –
это остаток от деления на порождающий
многочлен g(X).
Он находится в регистре после п
сдвигов
через (n
– k)
–
разрядный
регистр сдвига с обратной связью.
Заметим, что
первые n
– k
сдвигов по разрядам –
это просто заполнение регистра. Однако
никакой
обратной связи не будет, пока не будет
заполнен крайний справа разряд.
Следовательно, надо сократить цикл
деления, загружая входные данные
с выхода последнего разряда, как показано
на рисунке 1.

Рисунок 1– Кодирование с помощью (n – k) – разрядного
регистра сдвига
В крайнем левом разряде слагаемое обратной связи является суммой входных данных и крайнего правого разряда. Чтобы создавалась эта сумма, необходимо выполнение условия g0 = gn-k = 1 для произвольного порождающего многочлена g(X). Соединения схемы обратной связи соответствуют коэффициентам порождающего многочлена, который имеет следующий вид [2, 3]
 .
(1)
.
(1)
Процедура кодирования, использующее устройство, изображенное на рисунке 1 следующая:
При первых k сдвигах ключ 1 закрыт для передачи битов сообщения в (n – k) – разрядный регистр сдвига.
Ключ 2 установлен в нижнее положение для передачи битов сообщения на выходной регистр в течение первых k сдвигов.
После передачи k - гo бита сообщения ключ 1 открывается, а ключ 2 переходит в верхнее положение.
При остальных n – k сдвигах происходит очищение кодирующих регистров, биты четности перемещаются на выходной регистр.
Общее число сдвигов равно п, и содержимое выходного регистра представляет собой многочлен кодового слова
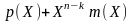 .
.
Кодеры несистематических циклических кодов: привести схемы и описать работу.
При передаче информации по каналу связи возможно ее искажение помехами. Одним из наиболее мощных методов борьбы с помехами является применение кодов, исправляющих и обнаруживающих ошибки.
Коды
задаются порождающей G
и проверочной H
матрицами, размерностью соответственно
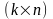 и
(
и
(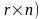 ,
удовлетворяющими условию, где
n-длина
кодового слова, k-число
информационных
,
удовлетворяющими условию, где
n-длина
кодового слова, k-число
информационных
Строками матрицы G являются k линейно независимых векторов длины n. При этом любое кодовое слово есть линейная комбинация строк G. Поэтому G называется порождающей матрицей кода.
Пространство
строк матрицы и минимальное расстояние
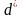 не изменяются при перестановке строк
матрицы, прибавлении к одной строке
другой, умноженной на скаляр. Поэтому
любая матрица G
может быть приведена к систематическому
виду
не изменяются при перестановке строк
матрицы, прибавлении к одной строке
другой, умноженной на скаляр. Поэтому
любая матрица G
может быть приведена к систематическому
виду
Свойство
цикличности состоит в том, что, если
слово
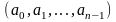 является кодовым, то его циклическая
перестановка
является кодовым, то его циклическая
перестановка
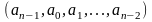 также является кодовым словом. Коды,
обладающие этим свойством, называют
циклическими.
также является кодовым словом. Коды,
обладающие этим свойством, называют
циклическими.
Циклический
код может быть задан генераторным
(порождающим) полиномом
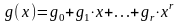 .
Полином a(x)
является кодовым словом тогда и только
тогда, когда делится на генераторный
полином без остатка:
.
Полином a(x)
является кодовым словом тогда и только
тогда, когда делится на генераторный
полином без остатка:

где v(x) – частное от деления a(x) на g(x) (полиному v(x) соответствует последовательность информационных символов).
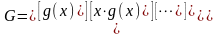
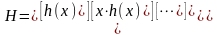
Умножения
сообщения
 на порождающую матрицу эквивалентно
перемножению
и
на порождающую матрицу эквивалентно
перемножению
и
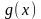 .
Действительно,
.
Действительно,
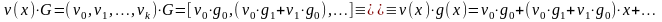
Схемная
реализация кодирующего устройства
базируется на схеме умножения многочленов.
Умножение многочлена
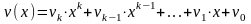 на
фиксированный многочлен
на
фиксированный многочлен
 ,
,

Произведение
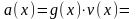
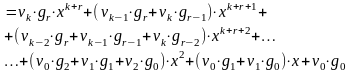
Предполагается,
что первоначально в триггерных ячейках
(рис. 4, а) – нули, коэффициенты
 известны, а на вход поступают коэффициенты
многочлена
v(x),
начиная со старших, после чего следует
r нулей.
Когда на вход подается первый элемент
многочлена
v(x)
, на выходе появится первый
известны, а на вход поступают коэффициенты
многочлена
v(x),
начиная со старших, после чего следует
r нулей.
Когда на вход подается первый элемент
многочлена
v(x)
, на выходе появится первый
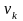 элемент произведения
элемент произведения
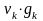 .
На втором шаге на выходе появляется
.
На втором шаге на выходе появляется
 ;
– в первой ячейке, во всех остальных
ячейках по-прежнему нули. Как видно из
схемы, выход равен
;
– в первой ячейке, во всех остальных
ячейках по-прежнему нули. Как видно из
схемы, выход равен
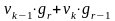 ,то
есть величине второго коэффициента
произведения. Дальнейшие операции
производятся аналогичным образом после
,то
есть величине второго коэффициента
произведения. Дальнейшие операции
производятся аналогичным образом после
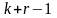 сдвигов в ячейках регистра
сдвигов в ячейках регистра
 ;
выход равен
;
выход равен
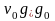 ,
то есть последнему коэффициенту
произведения
,
то есть последнему коэффициенту
произведения
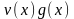 .
На последнем
.
На последнем
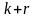 сдвиге в ячейках
сдвиге в ячейках
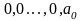 ;
на выходе
;
на выходе
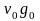 – последний коэффициент произведения.
– последний коэффициент произведения.
