Лабораторная работа № 1. Определение ускорения свободного падения для Астрахани при помощи физического маятника.

Ц ель работы: 1) изучение свободных колебаний на примере физического маятника; 2) определение ускорения свободного падения для Астрахани с помощью физического маятника.

Оборудование: 1) платформа на регулировочных ножках, закрепленная на ней стойка со шкивом; 2) часы, укрепленные на платформе; 3) физический маятник; 4) пластиковая втулка.

Краткая теория

Физический маятник. Физическим маятником называется тело, укрепленное на неподвижной горизонтальной оси, не проходящей через его центр тяжести, и способное совершать колебания относи­тельно этой оси (рис.1).

Докажем, что маятник, отклоненный на малый угол α от положения равновесия, будет совершать гармонические колебания. Обозначим через J момент инерции маятника относительно оси О. Пусть точка А является центром тяжести данного маятника. Силу тяжести можно разложить на две составляющие, одна из которых Р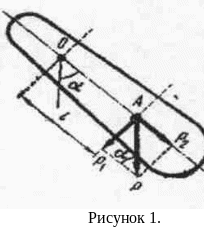 ₂ уравновешивается силой реакцией опоры. Под действием другой составляющей P₁ = Psin маятник приходит в движение. Так как угол  мал, то при малых отклонениях sin~.

Следовательно

P₁ = P = mg (1)

В соответствии с основным закон динамики для вращательного движения

Кроме того, из определения для момента силы относительно оси вращения известно, что момент .Поэтому для возвращающей силы Р₁ вращающейся момент выразится соотношением:

(2),

де  – угловое ускорение равное по определению второй производной угла поворота по времени

. (3)

l =ОA – плечо силы. Знак минус показывает, что действующая сила направлена в сторону противоположную положительному направлению отклонения маятника.

Подставляя (1) и (3) в формулу (2) получим:

(4)

Разделив обе части уравнения (4) на J.

(5)

Как показано в введении, решение уравнения (5) имеет вид  = Аcost. Однако, правильность решения можно доказать методом подстановки в данное уравнение (5) этого решения. Покажем, что частным решением последнего дифференциального уравнения является выражение вида:

 = Аcos t (6)

Для этого воспользуемся методом подстановки, показанным ранее в введении, то есть найдем первую и вторую производную от выражения (6) и введем обозначение

(7)

(8)

Из уравнений следует, что при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, частота которых зависит от массы маятника, момента инерции маятника относительно оси вращения и расстояния между осью вращения и центром инерции маятника. Сопоставим формулу для циклической частоты (7) с формулой для периода колебаний (6) получим, что период колебания физического маятника определяется выражением

При сопоставлении формул для математического маятника ( ) и для физического маятника ( ) следует, что математический маятник с длиной

будет иметь такой период колебаний, как и данный физический маятник. Величину l_пр называют приведенной длиной физического маятника. Таким образом, приведенная длина физического маятника — это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.

Точка на прямой, соединяющей точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника (см. точку 0' на рис. 2). Можно показать (рекомендуем это сделать в порядке упражнения), что при подвешивании маятника в центре качания 0' приведенная длина, а значит, и период колебаний будут теми же, что и вначале. Следовательно, точка подвеса и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания. На этом свойстве основано определение ускорения свободного падения с помощью, так называемого, оборотного маятника. Оборотным называется такой маятник, у которого имеются две параллельные друг другу, закрепленные вблизи его концов опорные призмы, на которых он может поочередно подвешиваться. Вдоль маятника может перемещаться и закрепляться на нем тяжелый груз. Перемещением грузов добиваются того, чтобы при подвешивании маятника за любую из призм период колебаний был одинаков. Тогда расстояние между опорными ребрами призм будет равно l_пр. В нашей работе в качестве такого маятника будет использован тяжелый стержень с отверстиями. Измерив период колебаний маятника и зная l_пр, можно найти ускорение свободного падения g по формуле

Т = 2π (9)