14.Минимальные многочлены и циклотомические классы, их связь с конечным полем, применение в теории кодирования.
15.Дуальные коды их свойства.
Рассматривая матрицы G и H , можно сделать следующие интересные выводы. Каждая из них содержит множество линейно независимых векторов , то есть каждая из матриц может рассматриваться как базис некоторого линейного пространства. Кроме того, каждое из этих пространств является подпространством векторного пространства, состоящего из всех наборов двоичных символов длиной n.
Скалярное произведение каждой строки матрицы G на каждую строку матрицы H равно нулю, то
H GT = 0 и G H T = 0 . (1.20)
Следовательно, можно "поменять ролями" эти две матрицы и использовать Н как порождающую матрицу, а G как проверочную матрицу некоторого другого кода.
Коды, связанные таким образом , называются дуальными друг другу, т.е., задав каким-либо образом линейный блочный код, мы автоматически задаем и второй, дуальный ему код. Правда, если исходный код был получен так, чтобы иметь минимальную избыточность при заданной исправляющей способности, то гарантировать хорошее качество дуального ему кода мы не можем . Такие коды обычно имеют исправляющую способность, одинаковую с исходными, но большую, чем у них, избыточность.
Например , если рассмотренный в качестве примера ( 7,4 )-код Хемминга имеет избыточность 7/4 и при этом позволяет исправлять одну ошибку в кодовом слове из 7 символов (об этом будем подробно говорить в следующих разделах настоящего пособия), то дуальный ему код ( 7,3 ) также исправляет одну ошибку на 7 символов, но уже имеет избыточность 7/3, то есть на 3 информационных символа содержит 4 проверочных. Дуальный код является низкоскоростным.
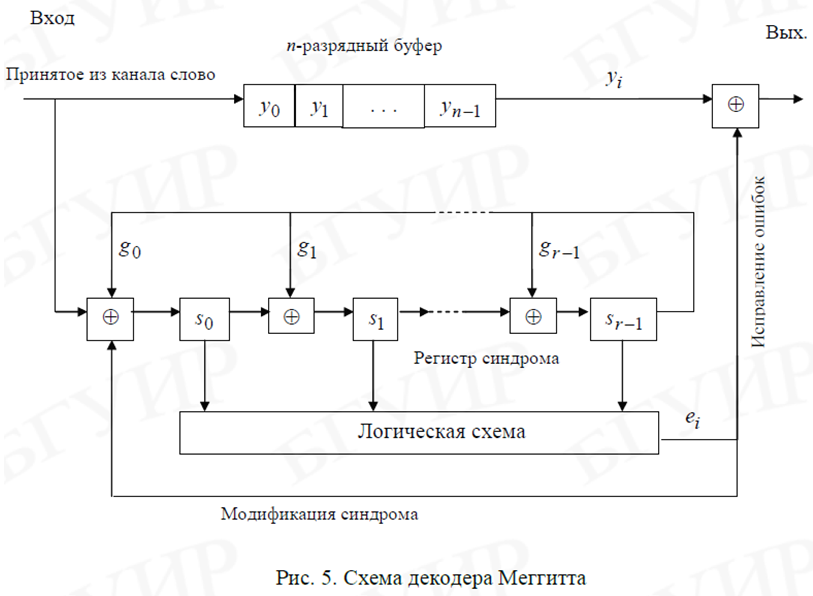
16.Методы вылавливания независимых и пачек ошибок.
17.Криптосистемы rsa: структура и принципы защиты информации.
В 1978 году R.L.Rivest, A.Shamir, L.Adleman опубликовали криптосистему с открытом ключом, которая стала известной как RSA система. Рассматриваемая система криптографии основывается на теореме Эйлера: Пусть a и n целые числа. Тогда
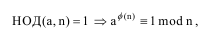
где НОД (a, n) – наибольший общий делитель чисел a и n, φ(n) - функция Эйлера
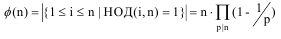
определяется для всех целых положительных n и представляет собой число чисел ряда 0,1,…, n - 1 взаимно простых с n.
Если существует каноническое разложение числа n
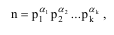
тогда
Алгоритм
RSA.
Каждый пользователь выбирает два простых
числа pu
и qu,
произведение которых образует число
.
Из
(2) следует,
что
Далее пользователь U определяет целое число e, 1< eu<φ(nu) , для которого НОД(eu, φ(nu)) = 1. С помощью алгоритма Евклида пользователь U вычисляет за 2log2φ(nu) шагов целое число du, удовлетворяющее сравнению
Пользователь U публикует числа eu и nu в открытой книге, но держит du в секрете. Числа pu и qu не публикуются.
Шифрование сообщения. Если пользователь A хочет передать сообщение m пользователю B (0 < m < nB), то A выбирает из открытой книги число eB и вычисляет зашифрованный текст:
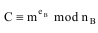
Расшифровка сообщения. Пользователь B восстанавливает сообщение
m из С, вычисляя
