9.Код Голея: параметры, доказательство оптимальности, схемы кодирования

Код Голея - совершенный двоичный код (23, 12, 7) (имеет длину n = 23, число информационных символов k = 12, кодовое расстояние d = 7) кода, способный исправлять до трех ошибок в словах длиной 23 символа.

Троичный код Голея : (11, 6, 5).

Расширенный двоичный код линейный код Голея (24, 12, 8) получается из кода Голея путем добавления ко всем кодовым комбинациям проверочного символа. Он тоже совершенный.

Линейный код Голея (23, 12) можно генерировать как циклический код посредством порождающего полинома g(p)=p¹¹+p⁹+p⁷+p⁶+p⁵+p+1. Кодовые слова имеют минимальное расстояние d_min=7.

Код является совершенным, т.к. удовлетворяет границе Хэмминга с равенством:

для двоичного блокового кода (n, k) с корректирующей способностью t граница Хэмминга определяется неравенством . Существование совершенного кода Голея подтверждается тем, что .

Кодирование. Из-за относительно небольшой длины (23) и размерности (12) кодирование м декодирование двоичного кода может выполняться табличным методом. Кодирование реализуется просмотром таблицы, содержащей список всех 2¹²=4096 кодовых слов, которые пронумерованы непосредственно информационными символами. Обозначим u информационный вектор размерности 12 бит и v – соответствующее кодовое слово (23 бита). Табличный кодер использует таблицу, в которой для каждого информационного вектора вычислен и записан синдром (11 бит). Синдром берется из таблицы и приписывается справа к информационному вектору. То есть для кодирования производится взаимно однозначное отображение из множества векторов u на множество векторов v.

Декодирование. Задачей декодера является оценка наиболее вероятного (обладающего минимальным Хэмминговым весом) вектора ошибок по принятому вектору. Процедура табличного декодирования:

1) выписать все возможные вектора ошибок e, вес Хэмминга которых не превышает 3;

2) для каждого вектора ошибок вычислить соответствующий синдром s;

3) записать в таблицу для каждого значения s соответствующий ему вектор e.

Кодирование как циклический код

Рисунок 1– Кодирование с помощью (n – k) – разрядного

регистра сдвига

10. Алгебро-геометрический подход

Пусть , а также конечное поле.

Положим (обычно ).

Пусть и пусть .

Определим отображение через оценку

которая отображает f(x) в вектор

где

Определение 2

q-ичный РС-код с параметрами [n,k], определяется как множество оценочных значений полиномов .

Множество P будем называть множество точек с.

Пример 1

Положим α=3 – примитивный элемент, тогда

Т.к.

Т.к.

Пример 2

Найдем для кода РС (15,11) над полем GF(16) для j₀=1, n-k=4=2t.

Решение:

Информационный многочлен – 11 символов поля.

Каждый символ несёт информацию в 4 бита, т.е. эквивалентная ёмкость информации сообщения будет 44 бита.

11.Алгоритм Берлекэмпа-Месси: его применение при декодировании помехоустойчивых кодов и при анализе линейной сложности криптографических функций

Алгоритм Берлекэмпа — Мэсси — алгоритм построения наиболее короткого регистра с обратными связями, порождающего m компонент синдрома S по правилу:

где ν - количество произошедших ошибок; r=ν+1, …, 2ν

и перестраивающего свою структуру в зависимости от возможной ошибки в структуре формируемого сигнала:

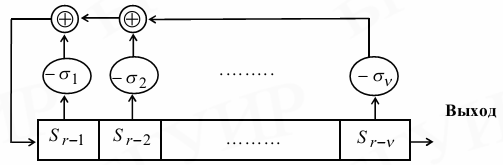
Для нахождения полинома локатора ошибок используется итерационная процедура. На каждой итерации вычисляется модель регистра с обратными связями, генерирующего первые r компонентов синдрома, где r – номер этапа. Длина регистра на r-м этапе обозначается Lr .

Теорема Берлекемпа–Месси. Пусть заданы компоненты синдрома S₁, … S_2t из некоторого поля, тогда при начальных условиях σ⁽⁰⁾(x)=1, B⁽⁰⁾(x)=1, L₀=1 выполняются следующие рекуррентные равенства, использующиеся для вычисления σ(x):

При выполнении таких условий полином σ(x) является многочленом наименьшей степени, коэффициенты которого удовлетворяют равенству

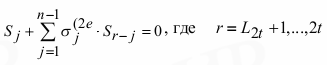
Граф-схема алгоритма Берлекемпа–Месси приведена на рисунке.

Задача декодера – найти полином Λ(z) или σ(z) минимальной степени ν , где ν - число ошибок, причём заранее не известное. Алгоритм Берлекемпа – Месси позволяет строить такую последовательность полиномов σ_j (z), j=1, 2, …m, в которой каждый последующий полином удовлетворяет большему числу уравнений. Одновременно итеративно вычисляется полином величин ошибок Ω(z).

Исходные данные - это m компонент синдрома S , где обычно b=1 . Начальные условия для полиномов σ(z), Ω(z), C(z), D(z) и переменной L задаются вначале.

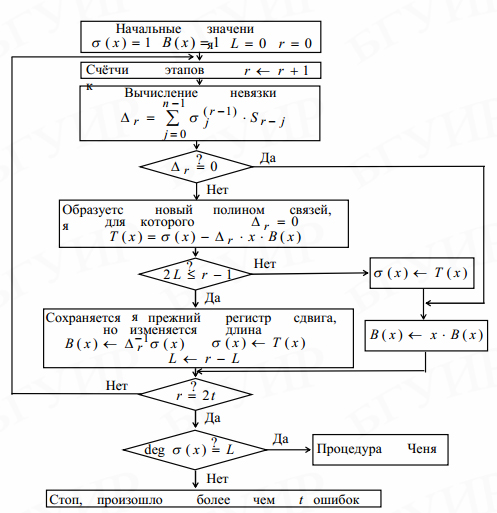
Алгоритм выполняется за m итераций. Если в процессе вычислений невязка Δ=0 , то полиномы σ(z) и Ω(z) не изменяются, в противном случае осуществляется их коррекция

где C_j-1(z) и D_j-1(z) - вспомогательные полиномы, взятые из предыдущего шага. На шаге j они формируются из следующих соображений. Если 2L_j-1 > j-1, то содержание регистров, хранящих эти вспомогательные полиномы, сдвигается: C(z)=z C(z); D(z)= zD(z) , а переменная L не изменяется. При 2L _j-1 ≤ j-1 указанные полиномы и переменная L трансформируются :

По окончании m итераций целесообразно выполнить проверку : deg σ(z)=L ; если это равенство несправедливо, то вырабатывается сигнал FLAG=1 защитного отказа от декодирования, так как принятое слово содержит более чем t ошибок.

Линейной сложностью конечной двоичной последовательности S_n называется число, которое равно длине самого короткого регистра сдвига с обратными связями, который генерирует последовательность, имеющую в качестве первых членов S_n . То есть с помощью алгоритма БМ составляется регистр сдвига, длина которого численно равна линейной сложности последовательности.

12. Вычисление синдрома ошибок помехоустойчивых кодов с помощью спектральных преобразований в поле Галуа.

Выберем и зафиксируем некоторое поле Галуа GF(q) с , примитивный элемент и параметр d. Рассмотрим информационный вектор длины k = n — d+ 1 = q — dc компонентами из GF(q). Поставим в соответствие вектору и вектор 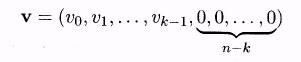длины п = q — 1, у которого первые k компонент совпадают с компо­нентами вектора и, а остальные компоненты — нулевые. Рассмотрим прямое преобразование Фурье вектора v в вектор V, определяемое (5.1) и удовлетворяющее теореме 5.2.1. Тогда справедлива следую­щая теорема: Теорема 5.3.2. Множество q^k векторов V в частотной области об­разует (п, k)-код Рида - Соломона. Теорема 5.3.3. Любой код Рида - Соломона является МДР кодом.

Декодирование кодов Рида - Соломона

Не трудно заметить, что при образовании кодов Рида - Соломона информационные символы можно размещать в любых k рядом стоя­щих разрядах вектора v. Из методических соображений отведем под информацию старшие компоненты V. В этом случае многочлен v(X) будет иметь вид а порождающий многочлен соответствующего кода Рида - Соломона имеет вид слова рассматриваемого кода Рида - Со­ломона являются прямым преобразованием Фурье множества век­торов V, то есть . В канале кодовому слову V добавляется вектор ошибки Е кратности Рассмотрим обратное преобразование Фурье принятого из канала слова В силу свойства линейности обратного преобразования Фурье имеем где - информационный вектор, лежащий во временной области, - обратное преобразование вектора ошибок. Так как п — k правых компонент вектора обрат­ного преобразования Фурье от V + E не зависят от кодового слова V, эти компоненты образуют синдром ошибок. Запишем этот синдром в виде где . Заметим, что синдром является некоторым «окном», через которое можно наблюдать обратное преобразование Фурье вектора ошибки Е. Обозначим индексы l ненулевых компонент вектора Е через . Определим вектор во временной области, прямое преоб­разование Фурье которого содержит нулевые компоненты для всех частот j, для которых . Проще всего такой вектор задать в виде многочлена локаторов ошибок 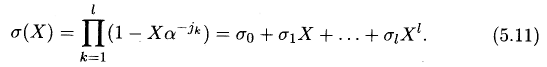Покомпонентное произведение прямого преобразования Фурье от многочлена σ(Х) на вектор ошибки Е в частотной области рав­но нулю, следовательно циклическая свертка во временной области вектора σ с вектором е также равна нулю Из (5.9) и (5.10) следует, что для определения компонент (согласно (5.11) σ₀ = 1), используя (5.12), мы можем составить си­стему d — 1 — l линейных уравнений с l неизвестными 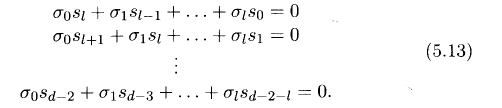Сложность, возникающая при решении системы уравнений (5.13) со­стоит в том, что кратность ошибки I нам заранее не известна.

Предположим, что все коэффициенты многочлена σ(Х) опреде­лены. В этом случае остальные k компонент вектора е, то есть ком­поненты во временной области, могут быть рекурентно определены, исходя из (5.12). Для определения компоненты e_fc_i нам достаточно решить урав­нение относительно , так как все остальные компоненты уже определены. На втором шаге мы уже можем составить уравнение для опреде­ления . Это уравнение имеет вид Рекурентно продолжая описанную процедуру, мы найдем все остав­шихся компоненты вектора е. Для определения информационного вектора v нам достаточ­но вычесть найденные компоненты из полу­ченных обратным преобразованием Фурье от R значений Самое замечательное в рассмотренном алгоритме состоит в том, что при его реализации не приходится находить ни корни многочлена σ (X) (локаторы ошибок), ни значения ошибок. Теперь общая картина процедуры декодирования ясна и ее можно сформулировать в виде пяти шагов. Шаг 1. Вычислить обратное преобразование Фурье принятого век­тора R = V + Е. Выделить во временной области и зашумленные компоненты информационного вектора v; Шаг 2. Найти σ(Х) из (5.13); Шаг 3. С помощью реку рентной процедуры вычислить компонен­ты ; Шаг 4. Найти информационный вектор v; Замечание. Рассмотренный алгоритм всегда исправляет и менее ошибок. В следующем разделе будет рассмотрен также слу­чай, когда число канальных ошибок превышает Для контроля правильности декодирования часто проводится следующий шаг. Шаг 5. Вычислить прямое преобразование Фурье вектора v, полу­чив при этом кодовый вектор (не всегда совпадаяющий с V).