7.Коды Рида-Маллера: схемы кодирования и алгоритмы декодирования.

Кодер РМ-2:

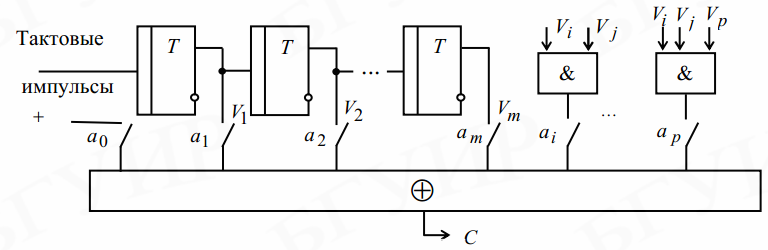
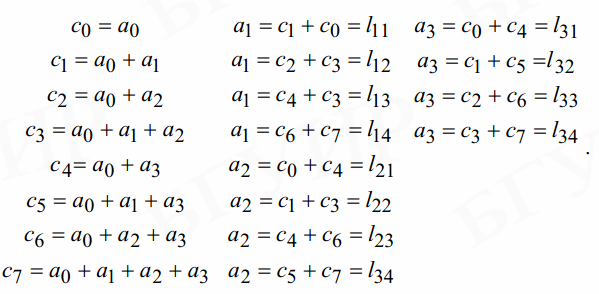
Мажоритарный декодер:

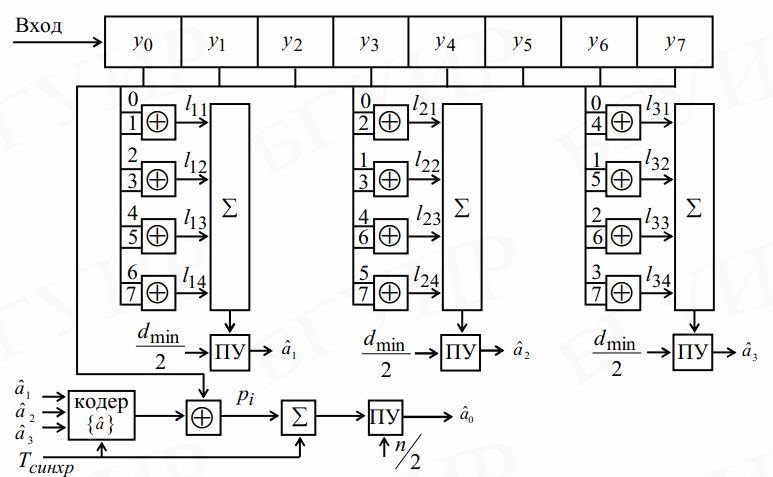
8. Коды Хэмминга: схемы кодирования и алгоритмы декодирования.

Коды Хэмминга имеют параметры (n; k) = (2^m–1; 2^m–1–m) и обычно задаются проверочной матрицей. Столбцами проверочной матрицы являются все ненулевые двоичные числа длиной m. Например, для кода (7; 4) проверочная матрица имеет следующий вид:

При m = r полные коды Хэмминга имеют, например, параметры (n; k)=(7;4), (15;11), (63;57).

Определим корректирующую способность кодов Хэмминга. Предварительно напомним, что весом w(a) слова a называется число ненулевых элементов, и в линейном коде расстояние d(a, b) между двумя словами a и b равно весу некоторого третьего слова a+b, т.е. d(a, b)=w(a+b).

Для определения минимального расстояния воспользуемся равенством

aН^Т = 0.

Предположим, что d(a, b)=1. Тогда в коде существует слово весом 1, что невозможно, так как для слов весом один aН^Т0. Теперь предположим, что d(a, b)=2. Тогда в коде существует слово весом 2, что также невозможно, поскольку никакие два столбца проверочной матрицы не дадут в сумме нулевой вектор. Следовательно, d(a, b)3. Простым подбором нетрудно найти слово весом 3, для которого aН^Т=0 (т.е. в матрице Н можно подобрать три столбца, которые в сумме дадут нулевой вектор). Окончательно получим d_min = 3, т.е. коды Хэмминга исправляют и обнаруживают соответственно любую одиночную и двойную ошибки. Поскольку все 2^m–1 векторов, задающих одиночные ошибки, принадлежат различным смежным классам, то этими смежными классами и кодовым пространством исчерпываются все 2^m смежных классов. Их образующими являются нулевой вектор и векторы единичного веса. Следовательно, коды Хэмминга являются совершенными.

Если передан вектор u, а принят вектор е+u, то синдром равен

(u+e)H^T = eH^T,

и для одиночных ошибок равен строке h^T, номер которой соответствует номеру искаженной позиции. Если векторы матрицы Н^Т упорядочены как двоичные числа (а не в приведенно-ступенчатой форме), то синдром говорит о номере искаженной позиции.

Пример. Построим кодирующее и декодирующее устройства кода Хэмминга (7; 4). Матрицы G и H имеют вид

Устройство кодирования (кодер) реализует нижеследующие уравнения и имеет вид (рис. 1)

a₅ = a₁ + a₃ + a₄,

a₆ = a₁ + a₂ + a₄,

a₇ = a₂ + a₃ + a₄.

Устройство декодирования (декодер) вычисляет синдром

A^*H^T = S=(S₁, S₂, S₃),

S₁ = a₁^*+ a₃^*+ a₄^*+ a₅^*, S₂ = a₁^* + a₂^* + a₄^* + a₆^*,

S₃ = a₂^* + a₃^* + a₄^* + a₇^*,

который реализуется блоком вычисления синдрома (БВС) (рис. 2).

Рис. 1. Кодирующее устройство кода Хэмминга (7; 4)

Вычисленный синдром поступает на селектор (дешифратор) синдрома, который по виду синдрома находит вектор ошибок E.

Если значение синдрома совпадает со значением i-го столбца матрицы H, то это значит, что ошибка произошла в i-м разряде. Если произошло две ошибки в i-м и j-м разрядах, то синдром S равен сумме i-го и j-го столбцов матрицы H. Поскольку это различные двоичные числа, то результат всегда не равен нулю и, следовательно, любая двойная ошибка будет обнаружена кодом Хэмминга.

Рис. 2. Блок вычисления синдрома кода Хэмминга (7; 4)

На рис. 3 представлен селектор, с помощью которого ошибки исправляются только в информационных разрядах. Как видно, селектор представляет собой неполный дешифратор.

Коррекция ошибок в принятом сообщении A^* по вектору ошибок осуществляется в корректоре на сумматорах по модулю два. Обобщенная структурная схема синдромного декодера кода Хэмминга имеет вид (рис. 3):

Рис. 3. Структурная схема декодера кода Хэмминга

На рис. 3 обозначены: БВС – блок вычисления синдромов, С – селектор, К – корректор. Коды Хэмминга могут задаваться и с помощью элементов поля Галуа.