25.Протокол Фейге-Фиат-Шамира.

Во многих криптографических системах возникает задача одной стороне A доказать знание секрета другой стороне B, причем сделать это так, чтобы сторона B после этого не знала сам секрет. То есть A демонстрирует знание какой-то информации не разглашая какой-либо части этой информации. В криптографии для этого используется протокол с нулевой передачей знаний или так называемое “доказательство с нулевым разглашением” (zero-knowledge proof). Как правило все протоколы с нулевым разглашением носят вероятностный характер. Это означает, что проверяющая сторона B никогда не может быть полностью уверена в знании стороной A секрета, но может убедиться в этом с точностью до любой заданной вероятности за конечное время.

Протокол Фейге-Фиат-Шамира

П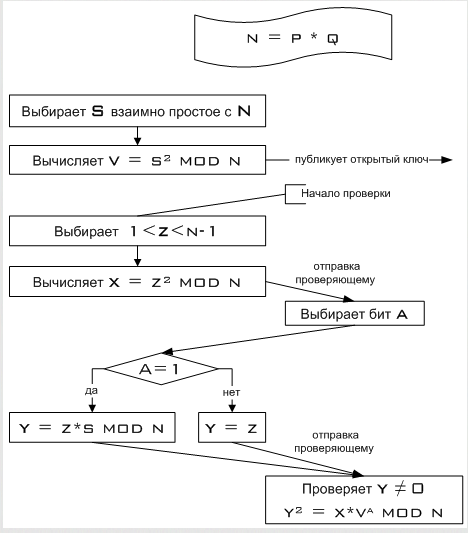 редполагается, что обе стороны заранее снабжены каким-то числом N = P * Q. При этом разложение N на простые множители считается неизвестным для всех участников протокола. Доказывающая сторона (Алёнка) выбирает секретное число S, взаимно простое с N, которое и является секретом. Далее Алёнка вычисляет значение V = S*S mod N и публикует значение V, объявляя его своим открытым ключом.

1. 1. Алёнка выбирает число Z от 1 до N-1

2. 2. Алёнка вычисляет число X и посылает его Борису

3. 3. Борис выбирает случайный бит А (0 или 1) и посылает его Алёнке

4. В зависимости от полученного бита А Алёнка вычисляет Y и передаёт его Борису

5. Борис проверяет Y

Эти шаги образуют один цикл протокола, называемый аккредитацией. Алёнка и Борис повторяют этот цикл много раз при разных случайных значениях Z и бита А до тех пор, пока Борис не убедится, что Алёнка действительно знает значение S.

26. Оценка уровня нелинейности и линейной сложности криптографической функции

Линейность той или иной математической задачи предопределяет эффективность методов и алгоритмов ее решения. При разработке и исследовании криптографических систем «нелинейность» (как общее понятие) используемых преобразований информации является их фундаментальным и неотъемлемым качеством.

Спектральные преобразования. Определим поле состоящее из элементов, примитивный элемент α и отображение f : → Булева функция (БФ) f(x) является представлением следа бинарной последовательност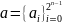и , если для всех i. Спектральное преобразование Уолша – Адамара (ПУ – А) функции f : → определяется через выражение

Если функция Ψ(λx) представляет собой след бинарной последователь-

ности Tr(λx), спектральное преобразование носит название Адамара. В том случае, если Ψ(λx)= <λ,x> , функцию 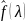называют преобразованием Уолша.

Оценка нелинейности булевых функций. Нелинейность БФ f определяется через расстояние Хэмминга d(f,a) как :=min{d(f,a), a- аффинная функция}, где d(f,a) – число x для которых f(x) ≠ a(x).

Уровень нелинейности может быть оценен через ПУ - А как

Булева функция удовлетворяет условию корреляционной иммунности порядка k если , для всех весов Хэмминга . Если функция f является к тому же балансной, то говорят, что она является k-резилентной функцией.