
- •Кодеры систематического циклического кода: матричного типа и на регистрах сдвига с обратными связями: привести схемы и описать работу.
- •2 Строка
- •Кодеры несистематических циклических кодов: привести схемы и описать работу.
- •3. Низкоскоростные корреляционные коды: методы и схемы кодирования.
- •4. Низкоскоростные коды: методы и схемы корреляционного декодирования.
- •5.Коды бчх: схемы кодирования и алгоритмы декодирования.
- •7.Коды Рида-Маллера: схемы кодирования и алгоритмы декодирования.
- •8. Коды Хэмминга: схемы кодирования и алгоритмы декодирования.
- •9.Код Голея: параметры, доказательство оптимальности, схемы кодирования
- •10. Алгебро-геометрический подход
- •11.Алгоритм Берлекэмпа-Месси: его применение при декодировании помехоустойчивых кодов и при анализе линейной сложности криптографических функций
- •14.Минимальные многочлены и циклотомические классы, их связь с конечным полем, применение в теории кодирования.
- •15.Дуальные коды их свойства.
- •16.Методы вылавливания независимых и пачек ошибок.
- •17.Криптосистемы rsa: структура и принципы защиты информации.
- •18.Криптоанализ системы rsa.
- •19. Криптосистемы на эллиптических кривых (целые числа): структура и принципы защиты информации.
- •2 0.Криптосистемы на эллиптических кривых (расширенные поля Галуа): структура и принципы защиты информации.
- •21. Шифр aes: структура и принципы защиты информации
- •22.Криптографические протоколы метод доказательства с нулевым разглашением знаний.
- •23. Шифр Вернама и сеть Фейстеля.
- •Расшифрование
- •Алгоритмическое описание
- •24.Режимы включения криптомодулей блочных шифров
- •25.Протокол Фейге-Фиат-Шамира.
- •26. Оценка уровня нелинейности и линейной сложности криптографической функции
- •27. Линейный и дифференциальный криптоанализ
- •28.Понятие хеш-функций и их свойства.
- •29.Алгоритмы создания и проверки электронной цифровой подписи (эцп). Алгоритмы
- •Симметричная схема
- •Асимметричная схема
- •Виды асимметричных алгоритмов эп
- •30. Сверточные коды: схемы кодирования и алгоритмы декодирования.
- •1. Пороговое декодирование
- •Жесткое пороговое декодирование сск
- •1.2. Мягкое пороговое декодирование сск
- •2. Вероятностное декодирование сверточных кодов
- •2.1. Декодер Витерби
- •2.2. Последовательное вероятностное декодирование сверточных кодов
23. Шифр Вернама и сеть Фейстеля.
Шифр Вернама, или одноразовый блокнот, был изобретен в 1917 году Мейджором Джозефом Моборном и Гильбертом Вернамом. В классическом понимании одноразовый блокнот является большой неповторяющейся последовательностью символов ключа, распределенных случайным образом. Отправитель использовал каждый символ ключа для шифрования только одного символа открытого текста. Для произведения шифротекста открытый текст объединяется операцией «исключающее ИЛИ» с ключом (называемым одноразовым блокнотом или шифроблокнотом). При этом ключ должен обладать тремя критически важными свойствами:
1) быть истинно случайным;
2) совпадать по размеру с заданным открытым текстом;
3) применяться только один раз.
Использование.
В
реальных системах сначала подготавливают
две одинаковые ленты со случайными
цифрами ключа. Одна остается у отправителя,
а другая передается "неперехватываемым"
образом например, курьером с охраной,
законному получателю. Когда отправитель
хочет передать сообщение, он сначала
преобразует его в двоичную форму и
помещает в устройство, которое к каждой
цифре сообщения прибавляет по модулю
два цифры, считанные с ключевой ленты.
На принимающей стороне кодированное
сообщение записывается и пропускается
через машину, похожую на устройство,
использованное для шифрования, которое
к каждой двоичной цифре сообщения
прибавляет (вычитает, так как сложение
и вычитание по модулю два эквивалентны)
по модулю две цифры, считанные с ключевой
ленты, получая таким образом открытый
текст. При этом, естественно, ключевая
лента должна продвигаться абсолютно
синхронно со своим дубликатом, используемым
для зашифрования.
Рис 1 изображена работа шифрования шифром Вернама
Главный недостаток данной системы - для каждого бита переданной информации должен быть заранее подготовлен бит ключевой информации, причем эти биты должны быть случайными. При шифровании большого объема данных это является серьезным ограничением. Поэтому данная система используется только для передачи сообщений наивысшей секретности.
Сеть Фейстеля (конструкция Фейстеля) — один из методов построения блочных шифров. Сеть представляет собой определённую многократно повторяющуюся структуру, называющуюся ячейкой Фейстеля. При переходе от одной ячейки к другой меняется ключ, причём выбор ключа зависит от конкретного алгоритма. Операции шифрования и расшифрования на каждом этапе очень просты, и при определённой доработке совпадают, требуя только обратного порядка используемых ключей. Шифрование при помощи данной конструкции легко реализуется как на программном уровне, так и на аппаратном, что обеспечивает широкие возможности применения. Большинство современных блочных шифров используют сеть Фейстеля в качестве основы.
Шифратор Дешифратор
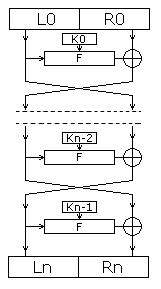
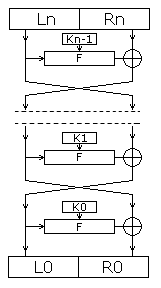
Шифрование
Рассмотрим случай, когда мы хотим зашифровать некоторую информацию, представленную в двоичном виде, как последовательность нулей и единиц.
Вся информация разбивается на блоки фиксированной длины. В случае, если длина входного блока меньше, чем размер, который шифруется заданным алгоритмом, то блок удлиняется каким-либо способом. Как правило длина блока является степенью двойки, например: 64 бита, 128 бит. Далее будем рассматривать операции происходящие только с одним блоком, так как с другими в процессе шифрования выполняются те же самые операции.
Выбранный блок делится на два равных подблока — «левый» (
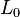 )
и «правый» (
)
и «правый» (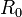 ).
).«Левый подблок» видоизменяется функцией
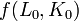 в
зависимости от раундового ключа
в
зависимости от раундового ключа 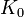 ,
после чего он складывается
по модулю 2 с
«правым подблоком»
.
,
после чего он складывается
по модулю 2 с
«правым подблоком»
.Результат сложения присваивается новому левому подблоку
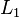 ,
который будет половиной входных данных
для следующего раунда, а «левый
подблок»
присваивается
без изменений новому правому
подблоку
,
который будет половиной входных данных
для следующего раунда, а «левый
подблок»
присваивается
без изменений новому правому
подблоку 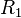 (см.
схему), который будет другой половиной.
(см.
схему), который будет другой половиной.После чего операция повторяется N-1 раз, при этом при переходе от одного этапа к другому меняются раундовые ключи ( на
 и т. д.)
по какому-либо математическому правилу,
где N —
количество раундов в заданном алгоритме
и т. д.)
по какому-либо математическому правилу,
где N —
количество раундов в заданном алгоритме
