- •2. Методы строительства на лессовых грунтах.(рисунки)
- •3. Опишите грунты по кривым гранулометрического состава (графики прилагаются).
- •4. Оцените инженерно-геологические условия площадки строительства по предлагаемому разрезу.
- •5. Укажите состав и примерный объем иг изысканий для одноквартирного жилого дома в г. Архангельске
- •6. Укажите состав и примерный объем иг изысканий для 5-ти этажного жилого кирпичного дома в г. Архангельске
- •Показатели, используемые для классификации пылевато-глинистых грунтов.
- •8. Дайте определение следующим физическим характеристикам грунтов: , s, , s, e, w. Укажите интервалы их значений для песков и торфов.
- •9. Глубина сезонного промерзания грунтов, классификация по степени пучинистости. Мероприятия по борьбе с морозным пучением.
- •10.Прочностные характеристики грунтов. Перечислите способы их определения в лабораторных и полевых условиях. Запишите основные закономерности.
- •11. Какая характеристика грунта является основной при расчете осадки основания. Ее определение в лабораторных и полевых условиях и интервалы изменения для различных грунтов.
- •12. Как вычисляют дополнительное давление в основании фундамента? Почему в расчете осадок используют именно эту величину, а не полное давление под подошвой?
- •13. Как определить вертикальное сжимающее напряжение в точке а, расположенной на глубине z в основании под углом отдельного фундамента.
- •14. Постройте линии равных вертикальных сжимающих и касательных напряжений в массиве грунта под равномерно распределенной гибкой полосовой нагрузкой
- •15. Основные принципы расчета осадки основания во времени.
- •17. Что называется грунтом, его составные элементы. Вода в грунте ее виды и свойства.
- •18. Как вычислить вертикальные напряжения в массиве грунта от его собственного веса в следующих случаях:
- •19. Какой расчет следует выполнить при возведении здания на склоне? Кратко изложите его методику.
- •20. Что обозначает и как определяется марка раствора.
- •21. Как определяют марку кирпича по прочности и морозостойкости. Какие марки по этим показателям существуют?
- •22. Как определяют марку бетона по прочности, морозостойкости и водонепроницаемости? Какие марки по этим показателям существуют?
- •23. Сроки схватывания и твердения вяжущих веществ: методы определения и наиболее характерные значения. Как изменить сроки схватывания и твердения?
- •24. Опишите следующие материалы: рубероид, толь, гидроизол, изол, пергамин. Назовите их основные свойства и условия применения. Как они маркируются?
- •25. Состав и примерный расход материалов для приготовления одного кубометра бетонной смеси. Как и почему изменяется качество бетона при изменении в/ц отношения?
- •26. Порядок расчета состава тяжелого бетона. К чему приведет полная или частичная замена (по массе) крупного заполнителя в тяжелом бетоне песком?
- •27. Назовите известные Вам кровельные и гидроизоляционные материалы. Кратко охарактеризуйте условия их применения.
- •28. Цемент технология производства, способы испытания, классификация.
- •29. Органические вяжущие. Их номенклатура, свойства, маркировка. Область применения.
- •30. Оцените инженерно-геологические условия площадки строительства. По предлагаемому разрезу.
- •31. Отдельные фундаменты мелкого заложения. Основные конструктивные решения и применяемые материалы.
- •32. Ленточные фундаменты под стены. Конструктивные решения, применяемые материалы. Условия применения прерывистых ленточных фундаментов.
- •35. Определение глубины заложения фундаментов с учетом конструктивных особенностей сооружения, включая наличие и глубину заложения соседних фундаментов.
- •36.Определение размеров подошвы центрально нагруженных фундаментов мелкого заложения.
- •37. Определение размеров подошвы внецентреннонагруженных фундаментов мелкого заложения.
- •38.Гидроизоляция фундаментов. Защита подвальных помещений от сырости и потопления подземными водами. Конструкция дренажей.
- •40. Какие методы расчета осадки фундаментов Вы знаете? Изложите метод послойного суммирования.
- •41. Как определить положение нижней границы сжимаемой толщи в различных методах расчета осадки фундаментов?
- •42. Классификация забивных свай по материалу, форме продольного и поперечного сечения, способу изготовления. Маркировка железобетонных свай.
- •44. Понятие о висячих сваях и сваях-стойках. Определение несущей способности свай-стоек.
- •4 5. Определение несущей способности висячих свай по таблицам сНиП. Понятие о негативном трении и его учет при определении несущей способности свай.
- •48. Определение границ условного фундамента при расчете осадок свайных фундаментов.
- •49. Определение несущей способности забивных свай по данным статистического зондирования грунтов.
- •50. Определение несущей способности свай по данным динамических испытаний. Методика испытаний.
- •51.Определение несущей способности свай по данным испытаний статистической нагрузкой. Методики испытаний.
- •52. Особенности расчета и устройства забивных свай в многолетнемерзлых грунтах.
- •53. Опускные колодцы. Условия применения, конструктивная схема и последовательность устройства. Классификация опускных колодцев по материалу, по форме в плане и по способу устройства стен.
- •54. Кессоны. Условия применения, конструктивная схема, последовательность производства работ.
- •55. Возведение заглубленных и подземных сооружений методом «стена в грунте». Технология устройства. Монолитный и сборный варианты.
- •56. Условия применения песчаных подушек при устройстве фмз. Основы их расчета и конструирования.
- •57. Поверхностное уплотнение грунтов укаткой, вибрацией и тяжелыми трамбовками. Понятие об оптимальной влажности уплотняемого грунта.
- •60. Усиление деревянных свайных фундаментов.
12. Как вычисляют дополнительное давление в основании фундамента? Почему в расчете осадок используют именно эту величину, а не полное давление под подошвой?
В![]() методе послойного суммирования осадка
вызывается дополнительным давлением
равным полному давлению под подошвой
фундамента р за вычетом вертикального
напряжения от собственного веса грунта
на уровне подошвы фундамента: ро
= р – σzg,o;
при планировке срезкой принимается
σzg,o
= γd,
при отсутствии планировки или планировке
подсыпкой; σzg,o
= γdn;
γ - удельный вес грунта, расположенного
выше подошвы фундамента; d
и dn
– глубина заложения фундамента от
уровня планировки и природного рельефа.
методе послойного суммирования осадка
вызывается дополнительным давлением
равным полному давлению под подошвой
фундамента р за вычетом вертикального
напряжения от собственного веса грунта
на уровне подошвы фундамента: ро
= р – σzg,o;
при планировке срезкой принимается
σzg,o
= γd,
при отсутствии планировки или планировке
подсыпкой; σzg,o
= γdn;
γ - удельный вес грунта, расположенного
выше подошвы фундамента; d
и dn
– глубина заложения фундамента от
уровня планировки и природного рельефа.
γ = ∑γihi/∑γi; Распределение по глубине дополнительных вертикальных напряжений уzр от внешнего давления ро принимается по теории линейно-деформируемой среды как в однородном основании. При подсчете осадок основание делится на «элементарные» слои, сжатие которых определяется от дополнительного вертикального напряжения σzр, действующего по оси фундамента в середине рассматриваемого слоя.
13. Как определить вертикальное сжимающее напряжение в точке а, расположенной на глубине z в основании под углом отдельного фундамента.
- От сосредоточенной силы находят по формуле Буссинески
В
полярных координатах
![]() ;
В прямоугольных координатах
;
В прямоугольных координатах
![]()
Где к – коэф-т , учитывающий распределение напряжений, опр-ся в зависимости от отношения r/z
-
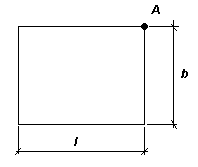
Под центром прямоугольной площадки
загружения σ zp=
α p (![]() ;
α – коэф-т, принимаемый в зависимости
от отношения размеров площади загружения
l/b и относительной глубины ξ=2z/b; р –
равномерно распределенная нагрузка).При
вычисление дополнительных напряжений
в основании фундамента в формулу вместо
р подставляют дополнительное давление
на основание Р0=р
– σzg0
, где σzg0 –
напряжение от собственного веса грунта
на уровне подошвы фундамента.
;
α – коэф-т, принимаемый в зависимости
от отношения размеров площади загружения
l/b и относительной глубины ξ=2z/b; р –
равномерно распределенная нагрузка).При
вычисление дополнительных напряжений
в основании фундамента в формулу вместо
р подставляют дополнительное давление
на основание Р0=р
– σzg0
, где σzg0 –
напряжение от собственного веса грунта
на уровне подошвы фундамента.
-
Под углом прямоугольной площади
загружения равны 1/4
напряжений под ее центром на половинной
глубине.
![]() ;
σ z=0,25
α p (α – коэф-т, принимаемый в зависимости
от отношения размеров площади загружения
l/b и относительной глубины ξ=z/b)
;
σ z=0,25
α p (α – коэф-т, принимаемый в зависимости
от отношения размеров площади загружения
l/b и относительной глубины ξ=z/b)
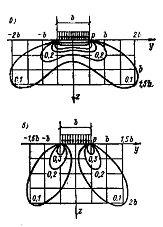
14. Постройте линии равных вертикальных сжимающих и касательных напряжений в массиве грунта под равномерно распределенной гибкой полосовой нагрузкой
При бесконечной длине полосы нагрузки l в каждом сечении, перпендикулярном ее продольной оси, будет одинаковая картина напряжений. Обычно рассматривают плоскую задачу, когда l:b ≥ 10. В таком случае определяют три составляющих: нормальные напряжения σz,, σу и касательные напряжения τуг. Указанные выше сечения остаются в процессе деформации плоскими (плоская деформация), следовательно, τХу = τхг = 0, а ух является функцией σz и σу. Если в изотропном теле во всех точках сечения, перпендикулярного продольной оси нагрузки, определить σz,, σу и τуг и соединить точки с одинаковыми значениями каждой из этих величин линиями равных напряжений, то получим своеобразные графики Последние показывают, что нормальные напряжения уz распространяются на значительную глубину (цифры на линиях указывают долю от нагрузки р), а нормальные напряжения σу и касательные напряжения τуг — преимущественно в пределах полутора-двух ширин полосы загружения. Из рисунка видно, что в вертикальных сечениях напряжения σz с глубиной убывают, это свидетельствует о том, что напряжения с глубиной рассеиваются на все большую площадь.
![]()