22. Понятие композиции. Теорема о числе композиций n.

Понятие композиции

В теории чисел композицией, или разложением, натурального числа называется его представление в виде упорядоченной суммы натуральных слагаемых. Слагаемые, входящие в композицию, называют частями, а их количество — длиной композиции.

В отличие от композиции, разбиение числа не учитывает порядок следования частей. Поэтому число разбиений числа никогда не превосходит числа композиций.

При фиксированной длине композиций в них иногда также допускают нулевые части.

Композиции и разбиения. Пусть стоит задача порождения разбиения положительного числа n в последовательность неотрицательных целых чисел {p₁,p₂,…,p_k}, так что p₁+p₂+…+p_k=n причем на р_i могут накладываться различные ограничения.

Если порядок чисел р_i важен, то (p₁,p₂,…,p_k) называется композицией n. Поиск композиций ведется с ограничением р_i>0.

Если k фиксировано, то такие композиции называются композициями n из k частей. При их поиске ограничение р_i>0 может сниматься, т.е. разрешается р_i=0.

Если порядок р_i не важен и р_i>0, то {p₁,p₂,…,p_k} является мультимножеством и называется разбиением n.

Поясним различие между композициями, композициями из k частей и разбиениями на следующем примере:

n=3,

композиции: (3), (1,2), (2,1), (1,1,1),

композиции из двух частей (р_i>0): (1,2), (2,1),

композиции из двух частей (р_i³0): (0,3), (1,2), (2,1), (3,0),

разбиения: {3}, {1,2}, {1,1,1}.

Теорема. Число композиций n равно 2^n-1.

Доказательство. Разделим отрезок длины n на n отрезков единичной длины с помощью (n-1) точки. Тогда композиции n взаимно однозначно соответствует пометка некоторых из точек разделения. Элементами композиции в этом случае будет расстояние между смежными точками. Например, композиция (2,2,1), n=5 представлена на рис.1.

SHAPE * MERGEFORMAT

2

2

1

0

1

2

3

4

5

Рис.1

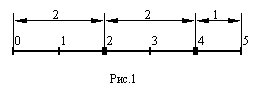
Следовательно, каждая композиция n соответствует способу выбора подмножества из (n-1) точек. То есть число композиций n равно 2^n-1.

Вопросы 23,24

Теорема. Число композиций n из k частей с ограничением р_i>0 равно   .

Доказательство. Представим композицию также как при доказательстве предыдущей теоремы. Каждая композиция n из k частей (р_i>0) соответствует способу выбора (k-1)-элементного подмножества точек из n-1 точек. То есть число таких композиций равно   .

Теорема. Число композиций n из k частей, если p_i³0 равно   .

Доказательство. Каждой композиции n из k частей при р_i³0 взаимно однозначно соответствует двоичный набор, такой, что первое слагаемое равно числу единиц, стоящих перед первым нулем в наборе, второе - числу единиц, стоящих перед первым и вторым нулями, и т.д. Пример такого представления композиции n=4, k=3 приведен в табл.1.

Длина набора равна n+k-1, число нулей равно k-1, следовательно, число наборов (искомых композиций) равно числу способов выбора k-1 мест для нулей из n+k-1 мест (   ) или тоже самое числу способов выбора n мест для единиц из n+k-1 мест (   ).

Таблица 1.

№	Композиция	Двоичный набор	Сочетание из 6 по 2
1	0+0+4	0 0 1 1 1 1	1 2
2	0+1+З	0 1 0 1 1 1	1 3
3	0+2+2	0 1 1 0 1 1	1 4
...	...	...	...
13	3+0+1	1 1 1 0 0 1	4 5
14	3+1+0	1 1 1 0 1 0	4 6
15	4+0+0	1 1 1 1 0 0	5 6

Доказательство данной теоремы можно было также получить путем установки взаимно однозначного соответствия между данными композициями и множеством всех сочетания из k элементов по n с повторениями.