19. Понятие сочетания. Теорема о числе сочетаний из n элементов по k. Свойства сочетаний.

Понятие сочетания

Определение. Неупорядоченные подмножества, содержащие k элементов из данного n-элементного множества, называют сочетаниями без повторений из n элементов по k, а их число обозначают символом   — сочетание.

Теорема 2 (о числе сочетаний без повторений). Число всех неупорядоченных k-элементных подмножеств n-элементного множества равно            (3) ○ Отметим, что N₀ = 1, то есть каждое множество X имеет лишь одно подмножество, не содержащее элементов (пустое множество), и Значит,  Количество сочетаний N_k и размещений   связаны равенством   так как упорядочить каждое сочетание (получив при этом размещение) можно k! способами. Отсюда  Используя (1), получаем

Свойства сочетаний.

1)

2)

3)

4)

5)

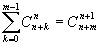
20. Понятие сочетания с повторениями. Теорема о числе сочетания с повторениями.

Понятие сочетания с повторениями

Сочетанием с повторениями называются наборы, в которых каждый элемент может участвовать несколько раз.

Теорема о числе сочетания с повторениями

Теорема.

Количество различных сочетаний из k объектов по n равно

C(n+k-1,n) = C(n+k-1,k-1)=(n+k-1)!/n!(k-1)!

21. Понятие размещения. Теорема о числе размещений.

Понятие размещения

В комбинаторике размещением называется расположение «предметов» (объектов) на некоторых «местах» при условии, что каждое место занято в точности одним предметом и все предметы различны. Более формально, размеще́нием (из n по k) называется упорядоченный набор из k различных элементов из некоторого множества различных же n элементов.

Примечание: заметим, что в случае, когда число мест, по которым размещают предметы, совпадает с количеством самих предметов, т. е. когда , рассматриваемая задача становится задачей о числе перестановок.

Теорема 1 (о числе размещений без повторений). Число размещений без повторений из n элементов по k определяется по формуле

(1)

○ Данная задача имеет решение только при k ≤ n. Отведем для элементов размещения строку ( 1;  2; ...;  k) длины k. Так как на первую позицию можно поместить любой из n элементов данного множества, а на вторую — любой из n – 1 оставшихся элементов, то, по правилу произведения, число различных способов для заполнения первых двух позиций строки равно n(n – 1). Далее аналогично: на третью можно поместить любой из n – 2 элементов, а, по правилу произведения, различных способов для заполнения первых трех позиций получается n(n – 1)(n – 2) и т.д. Окончательно получаем, что общее число строк длины k, формируемых из различных элементов n-элементного множества, равно = n∙(n-1)∙...∙(n-k+1) Отсюда получаем

Пример 1. Сколькими способами из 25 учеников класса можно выделить актив в следующем составе: культорг, физорг и редактор стенгазеты? ► Требуется выделить упорядоченные трехэлементные подмножества множества, содержащего 25 элементов, то есть найти число размещений без повторений из 25 элементов по 3. По формуле (1) находим