Вопрос26

Выбор структуры данных для хранения графа в памяти компьютера имеет принципиальное значение при разработке эффективных алгоритмов. Рассмотрим несколько способов представления графа.Пусть задан граф (например, рис. 44.1), у которого количество вершин равно n, а количество ребер – m. Каждое ребро и каждая вершина имеют вес – целое положительное число. Если граф не является помеченным, то считается, что вес равен единице.

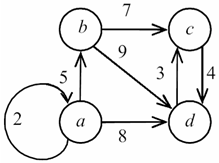
1. Список ребер – это множество, образованное парами смежных вершин (рис. 44.2). Для его хранения обычно используют одномерный массив размером m, содержащий список пар вершин, смежных с одним ребром графа. Список ребер более удобен для реализации различных алгоритмов на графах по сравнению с другими способами.

Рис. 44.2.  Список ребер графа

2 Матрица смежности – это двумерный массив размерности n x n, значения элементов которого характеризуются смежностью вершин графа (рис. 44.3). При этом значению элемента матрицы присваивается количество ребер, которые соединяют соответствующие вершины. Данный способ действенен, когда надо проверять смежность или находить вес ребра по двум заданным вершинам.

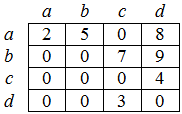
Рис. 44.3.  Матрица смежности графа

3. Матрица инцидентности – это двумерный массив размерности n x m, в котором указываются связи между инцидентными элементами графа (ребро и вершина). Столбцы матрицы соответствуют ребрам, строки – вершинам (рис. 44.4). Ненулевое значение в ячейке матрицы указывает связь между вершиной и ребром. Данный способ является самым емким для хранения, но облегчает нахождение циклов в графе.

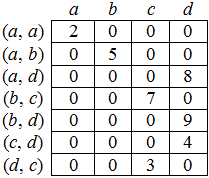
Рис. 44.4.  Матрица инцидентности графа

Вопрос27

Определение дерева графа: Связный неориентированный ациклический граф называется деревом, множество деревьев называется лесом.

Если рёбра, составляющие дерево, заменить ориентированными дугами, то получим ориентированное дерево. Для ориентированного дерева имеет смысл ввести понятие корня. Минимальное по мощности множество вершин ориентированного дерева, из которых существуют пути во все оставшиеся вершины, будем называть множеством корней.

Покрывающим (остовным) деревом графа G называется дерево, являющееся подграфом графа G и содержащее все его вершины.

Если граф G несвязен, то множество, состоящее из основных деревьев каждой компоненты, называется покрывающим (остовным) лесом.

Рассмотрим алгоритм построения покрывающего дерева, предложенный Дж. Краскалом в 1957 г.

Суть алгоритма состоит в просмотре в произвольном порядке рёбер исходного графа. При каждом просмотре в отношении соответствующего ребра принимается решение о том, будет или не будет оно включено в покрывающее дерево.

Алгоритм можно представить как процесс окрашивания рёбер. Пусть голубой цвет используется для окраски рёбер, включаемых в покрывающее дерево, а оранжевый – для окраски рёбер, не включаемых в это дерево.

В алгоритме при рассмотрении ребра осуществляется лишь проверка того, не образует ли данное ребро в совокупности с рёбрами, уже включенными в дерево (рёбрами, окрашенными в голубой цвет), цикл. Если результат проверки является положительным, то рассматриваемое ребро не включается в дерево (окрашивается в оранжевый цвет). В противном случае это ребро включается в дерево (окрашивается в голубой цвет).

В процессе работы алгоритма рёбра, включенные в дерево, составляют граф, имеющий один или несколько связных компонентов. Множество вершин, принадлежащих отдельному связному компоненту, для сокращения речи будем называть “букетом”. Некоторое ребро образует цикл с рёбрами, уже включенными в дерево, если обе его концевые вершины принадлежат одному и тому же связному компоненту (одному и тому же букету).

Работа алгоритма по построению покрывающего дерева заканчивается, когда количество рёбер, окрашенных в голубой цвет, становится равным числу, на единицу меньшему числа вершин графа, или, что то же самое, когда все вершины графа оказываются в одном букете.

Оба условия выхода относятся к случаю, когда исходный граф содержит покрывающее дерево, то есть является связным.

Если граф не является связным, то алгоритм заканчивается после раскраски всех рёбер графа. Голубые рёбра образуют покрывающий лес. Число деревьев в полученном лесе равно числу оставшихся букетов.

Сформулируем алгоритм построения покрывающего дерева.

Алгоритм 1. Алгоритм Краскала.

Начальная установка. Все рёбра исходного графа являются неокрашенными и ни один из букетов не сформирован.

Шаг 1. Выбрать любое ребро, не являющееся петлёй. Окрасить это ребро в голубой цвет и сформировать букет, включив в него концевые вершины выбранного ребра.

Шаг 2. Выбрать любое неокрашенное ребро, которое не является петлёй. Если в графе такого ребра не найдётся, то закончить процедуру: исходный граф не содержит покрывающего дерева.

После указанного выбора возможны четыре различных случая:

А. Обе концевые вершины выбранного ребра принадлежат одному и тому же букету. В этом случае ребро окрашивается в оранжевый цвет и производится возврат к началу шага 2.

Б. Одна из концевых вершин выбранного ребра принадлежит некоторому букету, а другая концевая вершина не принадлежит ни одному из уже сформированных букетов. В этом случае выбранное ребро окрашивается в голубой цвет и его концевая вершина, не принадлежащая ранее ни одному букету, включается в букет, которому принадлежит другая концевая вершина рассматриваемого ребра.

В. Ни одна из концевых вершин не принадлежит ни одному из сформированных букетов. Если имеет место такой случай, то необходимо окрасить ребро в голубой цвет и сформировать новый букет из его концевых вершин.

Г. Концевые вершины выбранного ребра принадлежат различным букетам. В этом случае необходимо окрасить выбранное ребро в голубой цвет, а оба букета, которым принадлежат его концевые вершины, слить в один новый букет.

Шаг 3. Если все вершины графа вошли в один букет, закончить процедуру, так как при этом условии голубые рёбра образуют покрывающее дерево. В противном случае вернуться к началу шага 2.

Изображение	Описание
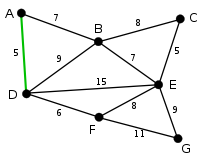
	Ребра AD и CE имеют минимальный вес, равный 5. Произвольно выбирается ребро AD (выделено на рисунке).
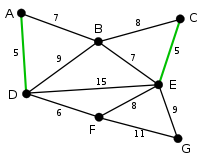
	Теперь наименьший вес, равный 5, имеет ребро CE. Так добавление CE не образует цикла, то выбираем его в качестве второго ребра.
	Аналогично выбираем ребро DF, вес которого равен 6.
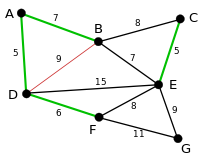
	Следующие ребра — AB и BE с весом 7. Произвольно выбирается ребро AB, выделенное на рисунке. Ребро BD выделено красным, так уже существует путь (зеленый) между B и D, поэтому, если бы это ребро было выбрано, то образовался бы цикл ABD.
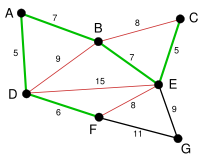
	Аналогичным образом выбирается ребро BE, вес которого равен 7. На этом этапе красным выделено гораздо больше ребер: BC, потому что оно создаст цикл BCE, DE, потому что оно создаст цикл DEBA, и FE, потому что оно сформирует цикл FEBAD.
	Алгоритм завершается добавлением ребра EG с весом 9. Минимальное остовное дерево построено.