ВОПРОС1. МНОЖЕСТВО является неопределимым понятием математики как точка, прямая и плоскость. Множество можно описать как совокупность некоторых объектов (элементов множества), объединенных по какому-либо признаку. Множества могут быть конечными (состоящими из конечного числа элементов) и бесконечными. Количество элементов в конечном множестве называется его мощностью и обозначается |А|. Множество нулевой мощности, не содержащее элементов, называется пустым и обозначается . Оно введено для удобства: лучше сказать, что множество пусто, чем объявить его несуществующим. В нашем примере множество студентов в аудитории может быть пустым. Множества, имеющие одинаковое количество элементов, называются равномощными. Класс всех рассматриваемых множеств называется универсальным множеством или универсумом (обозначается U). Мультимножество — в математике, обобщение понятия множества, допускающее включение одного и того же элемента по нескольку раз. Один из самых простых примеров — мультимножество простых множителей целого числа. Так, например, разложение числа 120 на простые множители имеет вид:

поэтому его мультимножество простых делителей —  .

Другой пример — мультимножество корней алгебраического уравнения. Например, уравнение  имеет корни  .

СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВА.

1. диаграммы Эйлера-Венна. Это графическое изображение множеств в универсуме. Универсум изображается прямоугольником, внутри которого располагаются множества, иллюстрирующиеся овалами. Результирующее множество выделяется штриховкой.

U

B

A

2. перечисление элементов. А={а1 а2 а3 а4 а5 а6}. Списком можно задавать только конечные множества. В данном случае последовательность элементов множества в произвольном порядке записывается в фигурных скобках. Множество целых чисел от n до m обозначается Аn..m

ПРИМЕР. D-3.. 3 ={ -3, -2, -1, 0, 1, 2, 3}

3. характеристический предикат. А={х| P(x)}. Это описание свойств элементов данного множества, где Р(х)- некоторое логическое выражение с логическим значением. Если результат Р(х) положителен (истинен), то элемент принадлежит множеству.

ПРИМЕР. D={nZ| -4<n<4}

Такие задания могут приводить к противоречиям, таким как парадокс Рассела: класс всех множеств, не содержащих себя в качестве элемента: А={B| BB}. Имеем: АА, тогда АА и обратно: АА, тогда АА. (Задача о лгунах: я всегда вру.)

4. порождающая процедура. А={х| х=F}. Здесь F – процедура, при работе которой появляются элементы множества.

ПРИМЕР. А={1, 2, 4, 8, 16, …}={n| 1A (nA2nA)}

Такое задание также называется рекурсивным. В курсе общей математики способ носит название математической индукции.

Еще одним примером порождающей процедуры, представляющим собой важный факт теории множеств, являются

ОПЕРАЦИИ НАД МНОЖЕСТВАМИ.

1. объединение множеств. Это множество, состоящее из элементов, которые принадлежат хотя бы одному из этих множеств.

АВ={ххА хВ}. Данная операция выполнима и для произвольного количества множеств (в т.ч. бесконечного):

ПРИМЕР. А={2, 1, 5, 7} В={-6, -7, 0, 1, 5} АВ={-7, -6, 0, 1, 2, 5, 7}

2. пересечение множеств. Это множество, элементами которого являются только те элементы, которые присутствуют в каждом из множеств. АВ={ххА хВ}. Эта операция также возможна с произвольным количеством множеств: .

ПРИМЕР. А={2, 1, 5, 7} В={-6, -7, 0, 1, 5} АВ={1, 5}

3. разность двух множеств. Это множество элементов, принадлежащих первому множеству и не являющихся элементами второго. А\В={ххА хВ}.

ПРИМЕР. А={2, 1, 5, 7} В={-6, -7, 0, 1, 5} А\В={2, 7}

4. симметрическая разность двух множеств. Это разность объединения этих множеств с их пересечением. А . В= (АВ)\( АВ) ={х (хА хВ)  (хА хВ)}.

ПРИМЕР. А={2, 1, 5, 7} В={-6, -7, 0, 1, 5} А\В={-7, -6, 0, 2, 7}

5. дополнение. Учитывая, что все множества образуют универсум, то дополнение –это множество элементов универсума, не являющиеся элементами данного множества. ={ххU хA}. В данном случае универсум должен быть либо задан, либо понятен из контекста задания.

Вопрос 2. Вектором (кортежем) в линейной алгебре и дискретной математике называют упорядоченный набор элементов. Это не есть определение вектора, поскольку целесообразнее это понятие считать основным.

Элементы, определяющие вектор, называются координатами или компонентами. Координаты нумеруются слева направо, а их число называется длиной или размерностью вектора. В отличие от элементов множества, координаты вектора могут совпадать. Координаты вектора заключаются в круглые скобки, например . Иногда скобки или запятые опускаются. Часто векторы длины 2 называются упорядоченными парами, длины 3 – тройками и т. д.

Определение. Два вектора равны, если они имеют равную длину и их соответствующие координаты равны. Иначе говоря, векторы и равны, если и .

Определение. Прямым произведением множеств А и В (обозначение ) называется множество всех упорядоченных пар , таких, что . В частности, если А=В, то обе координаты принадлежат множеству А, такое произведение обозначается А². Аналогично, прямым произведением множеств называется множество всех векторов длины п, таких, что .

Пример 4. Множество - это множество всех упорядоченных пар действительных чисел, геометрической интерпретацией которого служит декартова координатная плоскость.

Координатное представление точек плоскости было впервые предложено Р. Декартом и исторически является первым примером прямого произведения. Поэтому часто прямое произведение множеств называют декартовым произведением.

Пример 5. Даны множества и . Тогда есть множество обозначений клеток шахматной доски.

Вообще конечное множество, элементами которого являются какие-либо символы (буквы, цифры, знаки препинания, знаки операций и т. д.) называется алфавитом. Любые элементы множества в этом случае являются словами длины п в алфавите А. Например, десятичное целое число – это слово в алфавите цифр.

Определение. Проекцией вектора на некоторую ось называется его компонента (координата) с соответствующим порядковым номером (обозначается пр_ia). Например, проекция точки плоскости на 1-ю ось есть её абсцисса (первая координата).

Теорема 1.1. Мощность произведения конечных множеств равна произведению мощностей этих множеств: .

Следствие. .

Эта простая теорема и её следствие впоследствии широко используются в комбинаторике.

Вопрос3. Соответствия.

Определение. Соответствием между множествами А и В называется некоторое подмножество G их декартова произведения: .

Если , то говорят, что соответствует при соответствии . При этом множество всех таких называют областью определения соответствия , а множество соответствующих значений называются областью значений соответствия .

В принятых обозначениях, каждый элемент , соответствующий данному элементу называется образом при соответствии , наоборот, элемент называется прообразом элемента при данном соответствии.

Соответствие называется полностью определённым, если , то есть каждый элемент множества имеет хотя бы один образ во множестве ; в противном случае соответствие называется частичным.

Соответствие называется сюръективным, если , то есть если каждому элементу множества соответствует хотя бы один прообраз во множестве .

Соответствие называется функциональным (однозначным), если любому элементу множества соответствует единственный элемент множества .

Соответствие называется инъективным, если оно является функциональным, и при этом каждый элемент множества имеет не более одного прообраза.

Соответствие называется взаимнооднозначным (биективным), если любому элементу множества соответствует единственный элемент множества , и наоборот. Можно сказать также, что соответствие является взаимнооднозначным, если оно является полностью определённым, сюръективным, функциональным, и при этом каждый элемент множества имеет единственный прообраз.

Пример 1.

а) Англо-русский словарь устанавливает соответствие между множествами слов русского и английского языка. Оно не является функциональным, так как почти каждому русскому слову соответствует несколько английских переводов; оно, также, не является, как правило, полностью определённым соответствием, так как всегда существуют английские слова, не включённые в данный словарь. Таким образом, это частичное соответствие.

б) Соответствие между аргументами функции и значениями этой функции является функциональным. Однако оно не является взаимнооднозначным, так как каждому значению функции соответствуют два прообраза и .

в) Соответствие между расположенными на шахматной доске фигурами и занимаемыми ими полями является взаимно однозначным.

г) Соответствие между телефонами города Вязьмы и их пятизначными номерами обладает, на первый взгляд, всеми свойствами взаимнооднозначного соответствия. Однако оно, например, не сюръективно, поскольку существуют пятизначные числа, не соответствующие никаким телефонам.

сюръективное

соответствие

взаимооднозначное

соответствие

вопрос4. Функцией называется любое функциональное соответствие между двумя множествами. Если функция устанавливает соответствие между множествами А и В, то говорят, что функция имеет вид (обозначение ). Каждому элементу из своей области определения функция ставит в соответствие единственный элемент из области значений. Это записывается в традиционной форме . Элемент называется аргументом функции, элемент - её значением. Полностью определённая функция называется отображением А в В; образ множества А при отображении обозначается . Если при этом , то есть соответствие сюръективно, говорят, что имеет отображение А на В. Если состоит из единственного элемента, то называется функцией-константой. Отображение типа называется преобразованием множества А.

Пример 2. а) Функция является отображением множества натуральных чисел в себя (инъективная функция). Эта же функция при всех является отображением множества целых чисел в множество рациональных чисел.

б) Функция является отображением множества целых чисел (кроме числа 0) на множество натуральных чисел. Причём в данном случае соответствие не является взаимно однозначным.

в) Функция является взаимнооднозначным отображением множества действительных чисел на себя.

г) Функция не полностью определена, если её тип , но полностью определена, если её тип или .

Отображение f из множества X во множество Y – это правило, согласно которому каждому элементу x из X ставится в соответствие однозначно определенный y из Y. Отображение f из X в Y чаще всего обозначают следующим образом: f:X->Y. Областью определения отображения называется множество X; Областью значений отображения называется множество Y; f(x) – образ отображения; x – прообраз отображения; f^-1(y) – полный прообраз отображения (множество всех прообразов.); Множеством значений отображения E(f)=f(X) называют множество, состоящее из всей области определения множества; Инъективным отображением называется отображение, для которого из неравенства x1 и x2 следует неравенство f(x1) и f(x2). Аналогично можно сказать, что из x1=x2 следует, f(x1)=f(x2). Сюръективным называется отображение, для которого область определения совпадает с множеством значений отображения. Аналогично можно сказать, что полный прообраз не является пустым множеством для любого y из множества значений отображения. Биективным отображением называется отображение, обладающее признаками инъективности и сюръективности одновременно. Примеры отображений:

 Рассмотрим множество всех треугольников на плоскости. T – Множество площадей всех этих треугольников, R+ - множество всех положительных рациональных чисел. Правило f:T->R, согласно которому площадь каждого из треугольников на плоскости может быть выражена положительным рациональным числом является отображением.

 Для любого непустого множества X можно определить следующее правило f:X->X, согласно которому f(x)=x. Такое правило будет являться отображением, называемым так же тождественным.

инъекцией, если для любых элементов x1, x2 О X, для которых f(x1) = f(x2) следует, что x1 = x2. (рис. 7)

Сюръекцией (или отображением "на" ) называется отображение, при котором f(X) = Y (рис. 8).

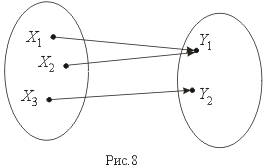
Биекция – это одновременно и сюръекция и инъекция (рис.9).

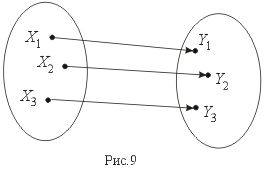
вопрос5. Число элементов множества ^ М называется его мощностью и обозначается |M|. Множества А и В называются эквивалентными, или равномощными, А В, если между их элементами можно установить взаимно-однозначное соответствие. Множество, содержащее конечное число элементов, называется конечным. Пустое множество является конечным и имеет мощность, равную нулю, т.е.  . Множество, не являющееся конечным, называется бесконечным. Бесконечное множество, эквивалентное множеству натуральных чисел N, называется счётным. В противном случае бесконечное множество будет несчётным. Множество называется бесконечным, если оно равномощно одному из своих собственных подмножеств

Если между двумя конечными множествами А и В существует взаимнооднозначное соответствие, то эти множества равномощны. Этот очевидный факт позволяет, во-первых, установить равенство мощности этих множеств, не вычисляя их. Во-вторых, часто можно вычислить мощность множества, установив его однозначное соответствие с множеством, мощность которого известна, либо легко вычисляется.

Теорема 2.1. Если мощность конечного множества А равна , то число всех подмножеств А равно , то есть .

Множество всех подмножеств множества М называется булеаном и обозначается . Для конечных множеств выполняется: .

Определение. Множества А и В называются равномощными, если между их элементами можно установить взаимнооднозначное соответствие.

Заметим, что для конечных множеств это утверждение легко доказать. Для бесконечных множеств оно определят само понятие равномощности.

Определение. Множество А называется счётным, если оно равномощно множеству натуральных чисел : .

Очень упрощённо можно сказать, что данное бесконечное множество является счётным, если для его элементов можно установить нумерацию с помощью натуральных чисел.

Без доказательства примем ряд важных фактов:

1. Любое бесконечное подмножество множества натуральных чисел является счётным.

2. Множество является счётным.

3. Множество рациональных чисел является счётным (является следствием из предыдущего утверждения).

4. Объединение конечного числа счётных множеств является счётным.

5. Объединение счётного числа конечных множеств является счётным.

6. Объединение счётного числа счётных множеств является счётным.

Все эти утверждения, как можно видеть, позволяют достаточно успешно устанавливать факт, что данное множество является счётным. Однако не всякое бесконечное множества является счётным; существует множества большей мощности.

вопрос6.Отношения служат одним из способов задания взаимосвязи между элементами множества. Наиболее изученными и чаще всего используемыми являются так называемые унарные и бинарные отношения. Для обозначения отношений мы будем использовать малые буквы греческого алфавита ρ, σ,τ и т.д.

Унарное (одноместное) отношение соответствует наличию какого-то определенного признака (свойства) у элементов множества X(например, признак «быть отрицательным» на множестве Z целых чисел). Все элементы, обладающие выделенным признаком, образуют некоторое подмножество ρ⊂X. Это подмножество ρ и называют унарным отношением на множестве X

Бинарные (двуместные) отношения используют как характеристику некоторой взаимосвязи между элементами множества X. Элементами бинарного отношения являются упорядоченные пары прямого произведения X×X, и, следовательно, само бинарное отношение может быть задано как некоторое подмножество прямого произведения ρ⊂ X×X. Так, например, на множестве M всех студентов университета можно ввести следующее отношение «принадлежности к одному факультету»: σ⊂ M×M и упорядоченная пара(a,b)∈σ тогда и только тогда, когда студенты a и b обучаются на одном факультете. Пример 1. Бинарные отношения на множестве .а) Отношение “ ” выполняется для пар и не выполняется для пары .

б) Отношение “иметь общий делитель, не равный единице” выполняется для пар и не выполняется для пар .

в) Отношение “быть делителем” выполняется для пар и не выполняется для пар .

СВОЙСТВА ОТНОШЕНИЙ.

Определение. Отношение называется рефлексивным, если для любого элемента имеет место .

Главная диагональ матрицы рефлексивного отношения содержит только единицы.

Определение. Отношение называется антирефлексивным, если ни для какого элемента не выполняется .

Главная диагональ матрицы рефлексивного отношения содержит только нули.

Например, отношения “ ” и “иметь общий делитель” являются рефлексивными. Отношения “ ” и “иметь сына” являются антирефлексивными. Отношение “быть симметричным относительно оси абсцисс” не является ни рефлексивным, ни антирефлексивным: точка плоскости симметрична сама себе, если лежит на этой оси, и не симметрична себе, если не лежит на ней.

Определение. Отношение называется симметричным, если для любой пары из отношения следует . Иными словами, отношение является симметричным тогда и только тогда, когда для любой пары оно выполняется в обе стороны (или вовсе не выполняется).Матрица симметричного отношения симметрична относительно главной диагонали: для любых .

Определение. Отношение называется антисимметричным, если из отношений и следует, что .

Отношение “быть симметричным относительно оси абсцисс” является симметричным: если первая точка симметрична второй относительно этой оси, то и вторая точка симметрична первой. Отношение “ ” является антисимметричным. Действительно, если и , это означает, что . Нетрудно убедиться в том, что отношение симметрично тогда и только тогда, когда .

Определение. Отношение называется транзитивным, если для любых из отношений и следует .

Отношения “быть равным”, “жить в одном городе”, “быть параллельным” являются транзитивными. Отношения “пересекаться”, “быть сыном” не являются транзитивными. Замечание. В отличие от отношений рефлексивности и симметричности, для отношения транзитивности не формулируется противоположного понятия (антитранзитивности).

полнота (линейность). Любые два элемента из множества А вступают в отношение хотя бы в одну сторону.

(a,bA) (a≠baRbbRa).