Способы построения диаграмм качества
1 способ: Непосредственная подстановка в характеристическое уравнение
Разложив данное уравнение можно выделить действительную и мнимую часть:
Можно
получить эти зависимости:
и
;
– при разных постоянных значениях K
Если НЭ однозначный, то можно использовать частотно-амплитудный метод.
При
неоднозначном НЭ коэффициенты
и
будут совпадать с теми коэффициентами,
которые мы рассматривали ранее.
2 способ: Гармоническая линеаризация НЭ
Периодический режим в ЗГЛНС:
Пример:
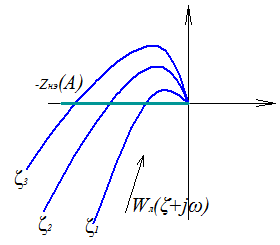
3 способ: Использование итерационных формул
Пусть
,
тогда:
;
;
;
По полученным значениям строим графики.
По диаграммам качества можно определить все показатели качества:
–
период
колебаний
определяем из диаграмм качества для
выбранного K.
– время, за которое значение меняется до
;
–
малая величина
- меняется мало,
Тогда:
- время, за которое менямпется до
меняется как угодно
,
В случае грубой оценки:
Рассмотрим половину периода:
,
Тогда амплитуда:
Пример: Рассмотрим структурную схему:
;
,
,
,
,
Построить
диаграммы качества по коэффициенту
Гармоническая линеаризация НЭ:
Характеристическое уравнение ЗГЛНС:
Из
Y получим:
(2)
Из
с учетом уравнения (2) получим:
(3)
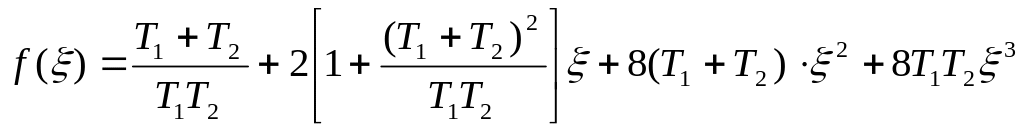(4)
По уравнениям (2) и (3) построим диаграмму качества
|
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||
|
a |
|
a |
|
a |
|
a |
|
a |
|
a |
1,7 2 3 4 |
0 22,6 93,1 163,6 |
1,8 2 3 4 2 3 4 |
0 5,1 30,6 56,1 |
1,9 2 3 4 4 |
0 1,1 15,4 29,7 |
2 2,1 3 4 5 5 |
0 1 11 21,2 31,8 |
2,2 3 4 5 |
0 4,8 10,7 16,4 |
2,4 3 4 5 |
0 2,4 6,4 10,4 , |
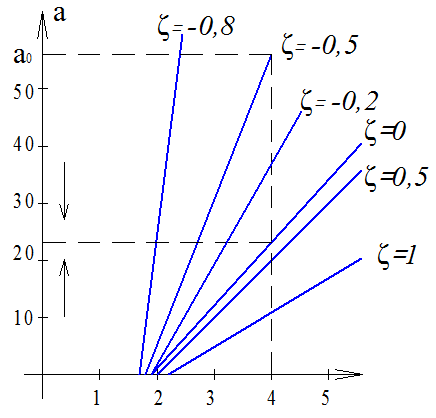
Рис.1
При процесс затухает, периодического режима нет
При в системе возникают автоколебания
Построим
при разных фиксированных значениях:
|
|
|
|
|
||||
а |
|
a |
|
a |
|
a |
|
|
-0,8 -0,5 -0,2 0 0,5 1 |
22,6 5,1 1,1 |
5,03 10,4 21,5 |
93,1 30,6 15,4 11 4,8 2,4 |
2,8 5,04 7 8,1 11,8 16,1 |
163,6 56,1 30 21,2 10,7 6,4 |
2,4 4,2 5,7 6,63 8,96 11,2 |
234 82,3 44 31,3 16,4 10,4 |
2,2 3,8 5,2 6 8 9,8 |
Рис.2
Для построения диаграммы качества
при
используется РИС.2 с учётом РИС при
фиксированном значении
.
Так как
напрямую от
не зависит, строим
.
Значения и a при разном берем из РИС.1, значение считаем по формуле (2)
|
|
|
|
|
|
|
|
a |
a |
a |
a |
a |
a |
2 3 4 5 |
- 80 114 135 |
- 50 65 75 |
22 30 40 46 |
16 19 21,2 26 |
14 16 19 24 |
11 12 14 17 |
Построим огибающую колебательного переходного процесса:
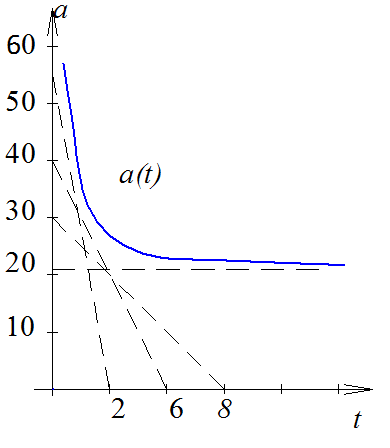
Построим касательные
Найдём показатели качества при :
- время затухания переходного процесса
m за t
