Использование кривой Михайлова для определения устойчивости периодического режима

– уравнение ЗГЛНС. (*)

- входной сигнал.

Уравнение кривой Михайлова:

, - частота, меняющаяся вдоль кривой Михайлова.

- частота гармонической линеаризации.

Выделим реальную и мнимую части:

(1)

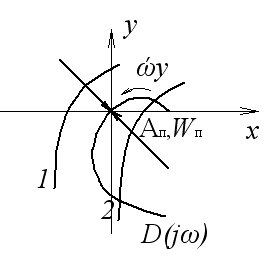
В начале координат .

В зависимости от изменения амплитуды, кривая принимает положение 1 или 2.

Если кривая принимает положение 1, видно, что годограф Михайлова последовательно проходит все квадранты, следовательно, САУ устойчива, процесс затухает.

Если кривая занимает положение 2, САУ неустойчива, процесс расходится.

Периодический режим устойчив, если при кривая Михайлова занимает положение 1, а при - положение 2, то есть процесс сходится с двух сторон к значению , поэтому он будет устойчивым.

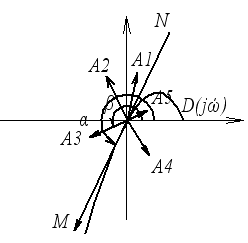
NM – касательная к кривой Михайлова. Направление касательной NM определяется частными производными.

, где и - действительные и мнимые части.

Направление перемещения начала координат при изменении амплитуды от периода

.

Условие устойчивости периодического режима можно определить следующим неравенством: , следовательно

- аналитический критерий устойчивости (2)

Использование критерия Гурвица для определения периодического режима и его параметров.

Рассмотрим уравнение (*).

Для , уравнение (*)может быть сведено к следующему виду:

(3)

- коэффициенты при различных степенях р.

Если нелинейный элемент однозначен, то коэффициент .

Для нахождения периодического режима используем условие нахождения системы третьего порядка на границе устойчивости.

Для

(4)

Сравним коэффициенты при равных степенях р:

Если , то .

Симметричные одночастотные вынужденные колебания.

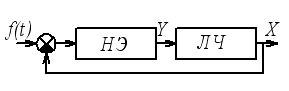
, - амплитуда входного воздействия.

Если выполнены условия гармонической линеаризации, то вынужденные колебания можно искать в следующем виде:

(1)

- частота входного воздействия;

- амплитуда вынужденных колебаний;

- фаза.

Пусть замкнутая нелинейная система приведена к следующему виду:

, (2)

где - передаточная функция от места приложения внешнего сигнала до выхода.

Уравнение (2) неоднозначное, поэтому выразим через .

(3)

(4)

Уравнение (4) представляет собой однородное уравнение замкнутой нелинейной системы.

Проведем гармоническую линеаризацию НЭ.

(5)

Вычисляем коэффициенты.

- коэффициенты.

Преобразуем уравнение (4) в уравнение (5)

(6)