Логическая система. Учет запаздывания.

Рассмотрим системы стабилизации объекта в среде без внешних воздействий.

Измерители вырабатывают сигналы и , которые подаются на логическое устройство. По данным сигналам выражается нелинейный закон управления, по данному закону исполнительное устройство вырабатывает на выходе момент М, который воздействует на объект управления.

Уравнение движения

, (1)

где - момент инерции,

- вращающий момент.

Пусть объект начал вращаться. Задача свести вращательные движения к колебательным.

На участке объект находится вблизи состояния равновесия, то есть управляющего воздействия не требуется.

Работу можно описать следующей таблицей.

	-	0	+
-	1	1	0
0	0	0	0
+	0	-1	-1

Фазовая траектория.

(2)

- создается моментом

(3) - уравнение фазовой скорости.

По участкам:

- парабола

- прямая линия с нулевым наклоном.

- парабола

Существует предельный цикл, на котором сходятся фазовые траектории.

При учитывании запаздывания , при включении и выключении исполнительного устройства, на фазовой плоскости линии переключения будут иметь наклон со следующими значениями.

Рассмотрим скользящий режим системы.

Линейная часть:

Нелинейный элемент:

Условие замыкания системы.

(1)

(2)

Уравнения линий срабатывания

На первом участке:

Получаем параболу, ветви которой направлены в отрицательную сторону , вершина данной параболы определяется начальными условиями.

На втором участке:

1. Фазовые траектории на отрезке АВ встречаются друг с другом.

2. Попав на отрезок СС, изображающая точка будет двигаться по отрезку к началу координат, так как скорость в этой точке равняется нулю.

3. Отрезок АВ – отрезок скользящего режима.

Характер движения на отрезке.

Нелинейная система автоматического регулирования второго порядка переходит в систему автоматического регулирования первого порядка.

На отрезке АВ система автоматического регулирования движется по экспоненте.

В точках А и В линия переключения является касательной к фазовой траектории.

Устойчивость нелинейных систем автоматического управления.

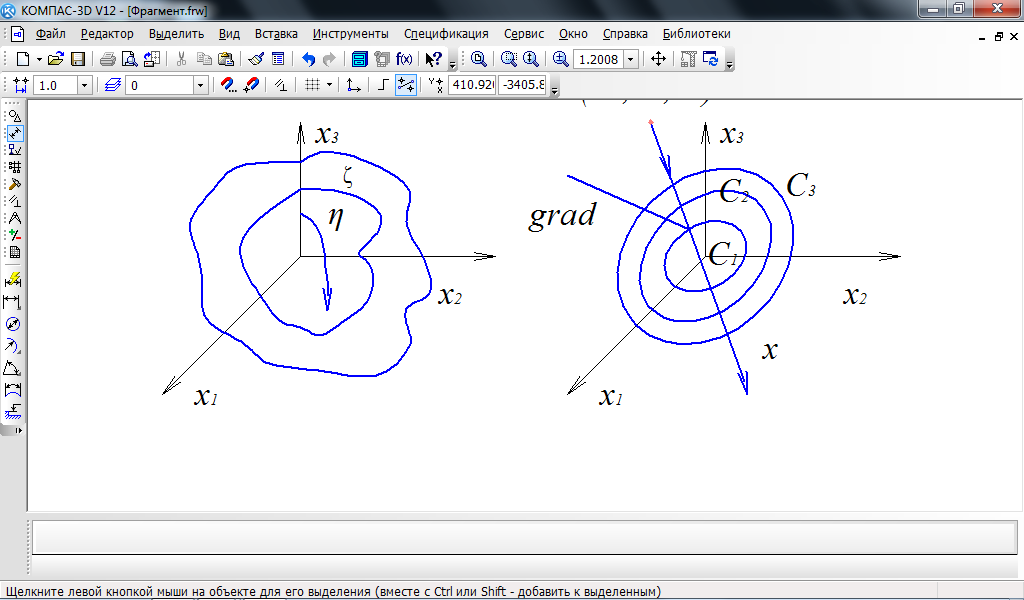
Невозмущенное движения системы – установившийся режим, возмущенное движение в системе – переходный процесс.

Невозмущенное движение в системе устойчиво, если найдется малая область , внутри которой можно определить область , зависящую от , что при любых начальных условиях, лежащих в области , переходный процесс будет таким, что не выйдет из области , при любом сколь угодно большом значении .

Динамическая система будет описываться:

(1)

- координаты состояния в отклонениях.

- функции, производные, содержащие нелинейности.

, если

Функция называется знакоопределяющей функцией в некоторой области вокруг начала координат, если во всех точках этой области она сохраняет постоянный знак и нигде не обращается в нуль, кроме самого начала координат.

Функция называется знакопостоянной в некоторой области вокруг начала координат, если во всех точках этой области она сохраняет постоянный знак, но может обращаться в нуль не только в начале координат, но и в других точках этой области.

Функция называется знакопеременной в некоторой области вокруг начала координат, если она может менять знак.

Функция Ляпунова: любую функцию можно назвать функцией Ляпунова, если в ней в качестве переменных взяты те же переменные, что и в системе (1) и которая обращается в нуль при равенстве координат нулю, то есть

- является функцией тех же координат, что и функция Ляпунова и к ней применимы все рассмотренные определения.

Вторая метода Ляпунова по устойчивости: если для системы, описанной системой уравнений (1) можно подобрать такую знакоопределяющую функцию , что производная от нее будет знакоопределяющей или знакопостоянной, но будет иметь знак противоположный знаку функции , то положение равновесия НСАУ устойчиво.

, вектор скорости .

Если будет отрицательной знакопостоянной функцией, то изображающая точка на фазовой траектории будет двигаться снаружи внутрь и необходимо проверить не останавливается ли она на одной из поверхностей до начала координат.

Чтобы положение равновесия было устойчиво, угол должен быть тупым.

Асимптотическая устойчивость (устойчивость систем в малом).

Устойчивость систем в большом.

Устойчивый предельный цикл.

Устойчивость систем в целом.

Функцию Ляпунова подобрать не всегда просто и требований к функции Ляпунова не много, поэтому вторая метода является необходимым, но и не достаточным условием устойчивости, то есть если выполняется теорема, система наверняка устойчива, если не выполняется, то не всегда устойчива.

Так как требования к функции Ляпунова малы, то для одной и той же системы можно подобрать несколько функций Ляпунова.

- постоянные.

Устойчиво внутри эллипса, вне – неустойчиво.