Нелинейные системы.
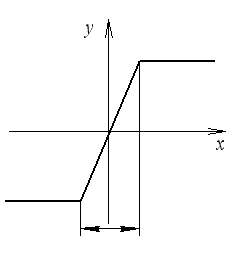
Любая динамика может описываться дифференциальным уравнением. Если динамическая система описывается нелинейным дифференциальным уравнением, то данная система является нелинейной.
Отметим ряд особенностей нелинейных САУ (НСАУ):
В НСАУ возможно несколько состояний равновесия. Часть из них может быть устойчивой, часть – неустойчивой.
В НСАУ возможны колебания с постоянной амплитудой и частотой. Параметры колебаний зависят только от свойств самой системы и не зависят от начальных условий. Такие колебания называются автоколебаниями.
Для НСАУ не применим метод суперпозиций или наложения сигнала.
В кривой переходного процесса НСАУ степень затухания
,
частота
непостоянны во времени.
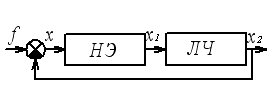
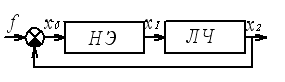
- входное воздействие,
- сигнал рассогласования (ошибка),
- входная величина линейной части,
- выходная величина НСАУ.
Пример1:
Пример2:
=
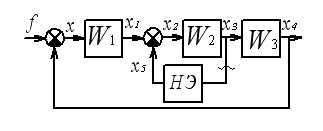Характеристики линейной части (ЛЧ):
дифференциальное уравнение
передаточная функция
уравнение в операторной форме
уравнение в оригиналах
временные характеристики
частотные характеристики
Виды нелинейных элементов (НЭ):
однозначной нелинейности,
неоднозначной нелинейности.
НЭ однозначной нелинейности:
ограничение, насыщение
ограничение зоны нечувствительности
идеальное реле
реле зоны нечувствительности
зона нечувствительности
НЭ неоднозначной нелинейности:
прямой гистерезис
трехпозиционное реле с зоной нечувствительности и гистерезисом
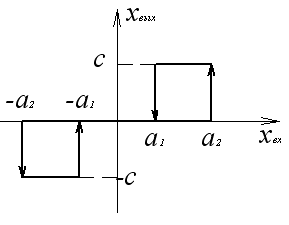
Исследование нелинейных систем использует следующие методы:
фазовый метод;
частотно–амплитудный метод;
графоаналитический метод;
моделирование нелинейных систем.
Фазовый метод.
Фазовое пространство – пространство, по координатным осям которого отложено значение переменной, значение скорости переменной, значение ускорений различных порядков.
Фазовая плоскость – плоскость, по координатным осям которого отложены значения переменной и скорости переменной.
Состояние системы в любой момент времени можно оценить двумя координатами.
Точка М – изображающая точка.
При изменении состояния системы изменяется положение точки М, то есть точка М перемещается по какой-либо траектории – фазовой траектории.
В установившемся режиме
,
то есть начало координат соответствует
точке установившегося режима.
Фазовые траектории установившихся систем должны сходиться к началу координат.
Пусть уравнение динамики задано в
следующем виде:
.
(1)
- значение
в момент времени
;
- значение
в момент времени
.
, - начальные условия.
(2)
Если в системе (2)
и
- нелинейные функции – отличны от нуля
одновременно
,
то уравнение фазовой скорости определено
в любой момент времени.
Математически фазовую скорость можно получить из уравнений (1) и (2), поделив второе уравнение на первое системы (1).
– уравнение фазовой скорости
(3)
Семейство фазовых траекторий – решение уравнений фазовых скоростей.
Если
,
то в данном случае фазовая скорость не
определена (появляются особые точки).
Фазовая плоскость, заполненная фазовыми траекториями при различных начальных условиях, образует фазовый портрет системы.
Фазовая скорость – касательная к фазовым траекториям.
Линия, соединяющая точки фазовых траекторий с одинаковым наклоном касательных называется изоклиной.
- уравнение изоклины.
Виды особых точек (на примере звена второго порядка):
комплексно сопряженные
1)
Начало координат – особая точка, устойчивый фокус.
2)
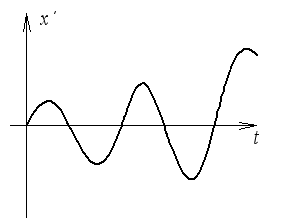
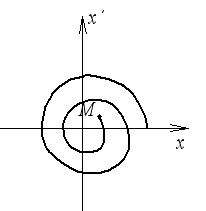
Неустойчивый фокус.
чисто мнимые
Начало координат – центр.
действительные
1)
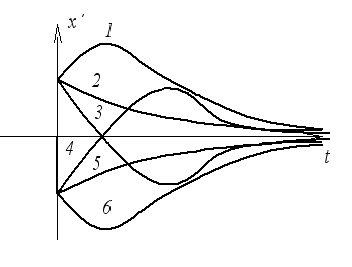
Начало координат – устойчивый узел.
2)
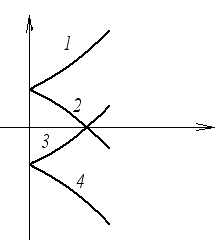
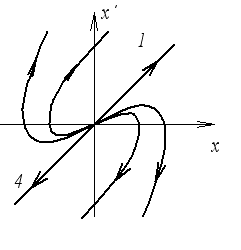
Начало координат – неустойчивый узел.
3)
Начало координат – седло.
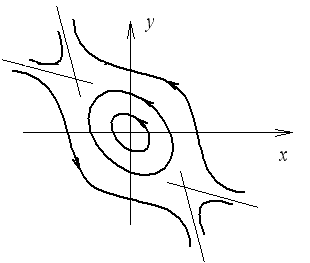
Особые линии фазовой плоскости:
предельный цикл
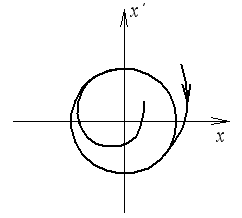
Устойчивый предельный цикл.
Внутренний устойчивый предельный цикл, внешний неустойчивый предельный цикл.
Предельный цикл устойчивый, если при любых начальных условиях фазовые траектории сходятся к кривой предельного цикла, неустойчив, если расходится.
Неустойчивый предельный цикл.
Устойчивый предельный цикл.
сепаратриса
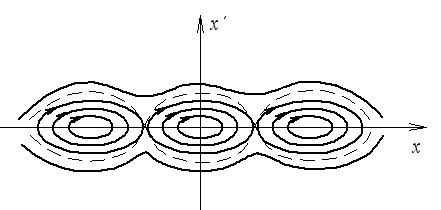
Пример – математический маятник.
Внутренние линии – маятник качается, внешние – вращается.
Сепаратриса – линия на фазовой плоскости, которая разделяет различные состояния системы, при этом она не замкнута.
особый отрезок
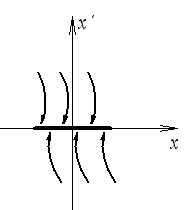
Пример 1: релейная следящая система
P – редуктор;
П1, П2 – потенциометры;
- входной сигнал
;
- выходной сигнал
.
;
;
Уравнение линейной части:
Для определения возможности автоколебаний
в замкнутой НСАУ полагаем, что
.
(1) – уравнение линейной части в
операторной форме.
(2) – уравнение нелинейной части в
дифференциальной форме.
Уравнение нелинейного элемента:
(3)
- нелинейная функция, которая зависит
от вида нелинейности.
Уравнение замкнутой НСАУ:
(4)
1)
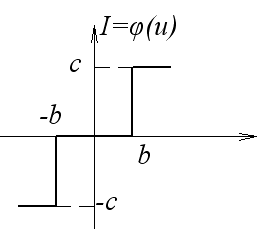
(5)
По уравнениям (4) и (5) составим уравнения по участкам.
1 участок:
2 участок:
3 участок:
Линии, разделяющие фазовую плоскость
на области с разными характером,
называются линиями переключения
.
Определим характер фазовых траекторий по участкам.
1 участок:
- уравнение фазовой скорости.
Начальные условия:
;
2 участок:
3 участок:
2)
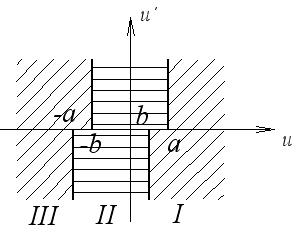
Пример.
Определить особые точки и их вид.
Особая точка – точка, в которой фазовая скорость не определена.
А(0;0), B(-1;1), C(1;-1)
(0;0)
А(0;0) – особая точка типа центр
(1;-1)
«седло»
(-1;1)
«седло»
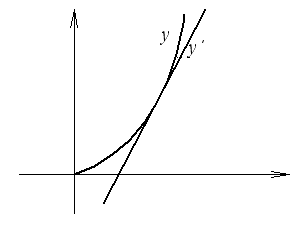
Линеаризовать уравнение статики объекта
в окрестности точки
,
.
Одним из методов линеаризации является разложение функции в ряд Тейлора в окрестности заданной точки с последующим отбрасыванием нелинейных членов.
Линеаризованная характеристика получается в результате отбрасывания членов 2-го порядка и выше.
Далее рассчитаем коэффициенты линеаризованного уравнения.
Система описывается:
Исходную нелинейную систему необходимо линеаризовать методом разложения в ряд Тейлора в окрестностях точек состояния равновесия. В результате линеаризации получаем линейную систему дифференциальных уравнений.
Устойчивый узел
Неустойчивый узел
На вход нелинейного элемента подаются гармонические колебания
Чтобы вывести эквивалентную амплитудно-фазовую характеристику нелинейного звена, необходимо провести гармоническую линеаризацию.
Гармоническая линеаризация основана на том, что на вход нелинейного звена подается гармонический сигнал, на выходе образуется периодический сигнал сложной формы, который может быть разложен в ряд Фурье.
В результате линеаризации ряда Фурье остается только первая гармоника.
Коэффициенты определяются по следующим формулам:
где
,
F(y)-
статическая характеристика нелинейного
звена, А – амплитуда входного сигнала,
которую необходимо учитывать, так как
эквивалентные частотные характеристики
НЭ зависят от амплитуды входного сигнала,
а не от частоты.
В алгебраической форме
Так как статические характеристика
симметрична относительно
то формулу можно переписать в следующем
виде.
Метод гармонической линеаризации.
(1)
Богалев и Крылов предложили метод определения периодических режимов системы, движение в которой близко к синусоидальному, основанный на том, что в силу фильтрации или резонансных свойств линейной части системы при расчете периодических режимов в нелинейных системах, выходной сигнал нелинейного элемента при расчетах можно принимать только основную первую гармонику.
- коэффициенты ряда Фурье.
- амплитуда выходного сигнала.
(2)
(3)
(4)
(1’)
Для однозначной нелинейности
То есть замена нелинейного элемента линейным есть гармоническая линеаризация.
- коэффициент передачи гармонически
линеаризованного нелинейного элемента.
Вместо уравнения (1’) получи либо уравнение (3), либо уравнение (4), в зависимости от вида нелинейности.
Для неоднозначной характеристики
существует
.
Вторая часть учитывает запаздывание реле, выраженное отрицательным коэффициентом .
Уравнения (3) и (4) – линейные уравнения.
Так как на входе и выходе после гармонической линеаризации нелинейного элемента одиночные сигналы, то
;
Заменим
на
,
Коэффициенты гармонической линеаризации.
;
;
Е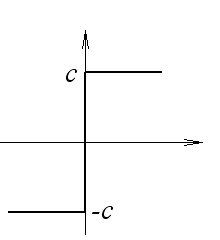
сли
;
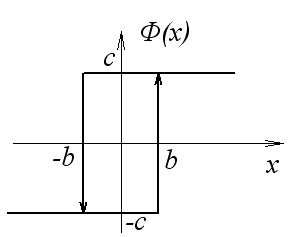
Рассмотрим нелинейность, которая аппроксимируется полиномом не выше четвертого порядка.
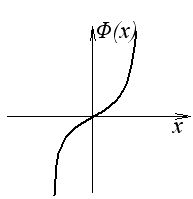
Если степень
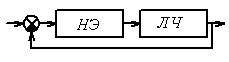
Гармоническая линеаризация
