Основные характеристики вариационного ряда

Характеристики вариации (рассеивания)

Средние, или характеристики центральной тенденции

Характеристики дифференциации и концентрации

Характеристики формы распределения

Вариационные ряды дают возможность установить характер распределения единиц совокупности по тому, или иному кол-му признаку с помощью расчета 4-х видов характеристик (групп показателей), указанных на рис.5.3.

Средняя арифметическая по данным интервального вариационного ряда рассчитывается методом моментов по формуле

, или , (5.1)

где А – середина одного из центральных интервалов, имеющего, как правило, наибольший вес;

h – величина интервала;

m´- момент первого порядка, т. е. средняя арифметическая из значений :

. (5.2)

17 Показатели вариации.

При определении общего характера распределения важнейшей задачей является оценка степени его однородности. Однородность статистических совокупностей характеризуется величиной

вариации значений признака.

Отметим, что вариация, т.е. несовпадение уровней значений признаков у единиц совокупно-

сти, имеет объективный характер, ибо конкретные условия, в которых находится каждая из изуча-

емых единиц совокупности, а также особенности их собственного социально-экономического раз-

вития, выражаются соответствующими числовыми уровнями значений признаков (показателей).

Вариация помогает познать сущность изучаемого явления.

Для измерения вариации в статистике применяют несколько способов.

Наиболее простым является расчет показателя размаха вариации (R) как разницы между

максимальным (Хmax) и минимальным (Хmin) наблюдаемыми значениями признака по формуле

R=Xmax-Xmin

Размах вариации улавливает только крайние отклонения значений признака, но не отражает

отклонений от средней величины всех вариант в ряду. Чем больше размах вариации, тем менее

однородна исследуемая совокупность.

Средние отклонения значений признаков каждой единицы совокупности от среднего значе-

ния признака в целом отражают показатели вариации. Показатели вариации используют для

оценки степени однородности исследуемой совокупности по варьирующему признаку и типично-

сти средней величины.

Простейший показатель такого типа – среднее линейное отклонение, представляющее собой

среднее арифметическое значение абсолютных отклонений признака от его среднего уровня.

Среднее линейное отклонение (d) по не сгруппированным данным рассчитывается по

Формуле

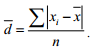
Среднее линейное отклонение (d) по сгруппированным данным рассчитывается по форvуле

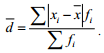
Чем меньше среднее линейное отклонение, тем более однородны значения признака изучае-

мого явления.

Основной недостаток показателя среднего линейного отклонения заключается в том, что при

его расчетах пренебрегают знаками, следовательно, конечный результат получается со значитель-

ной погрешностью. Для того чтобы расчет был более точным, определяют средний квадрат откло-

нений (дисперсию), представляющий собой средний квадрат отклонений значений признака от его среднего уровня.

Дисперсия (σ2) по не сгруппированным данным рассчитывается по формуле

Дисперсия (σ2) по сгруппированным данным рассчитывается по формуле

Среднее квадратическое отклонение (σ) рассчитывается по формуле

Среднее квадратическое отклонение является абсолютной мерой вариации и зависит не

только от степени вариации признака, но и от абсолютных уровней вариант и средней, что не позволяет непосредственно сравнивать средние квадратические отклонения вариационных рядов с разными уровнями. Оно выражается в тех именованных числах, в которых выражены варианта и

средняя величина.

Для сравнительной характеристики вариационных рядов с разными уровнями по степени

надежности их средней величины и однородности исследуемых совокупностей рассчитывается

относительная мера вариации – коэффициент вариации.

Коэффициент вариации (V) рассчитывается по формуле

Чем больше значение коэффициента вариации, тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна (типична) средняя величина.

Вместе с тем, следует помнить, что оценка степени интенсивности вариации возможна только для каждого отдельного признака и совокупности определенного состава. Так, для совокупности сельхозпредприятий вариация урожайности в одном и том же природном регионе может быть оценена как слабая, если V < 10 %, умеренная при 10 % < V <25 % и сильная при V > 25 %. Напротив, вариация роста в совокупности взрослых мужчин или женщин уже при коэффициенте, равном 7 %, должна быть оценена и восприниматься людьми как сильная. Таким образом, оценка интенсивности вариации состоит в сравнении наблюдаемой вариации с некоторой обычной ее интенсивностью, принимаемой за норматив. Если различия в урожайности, заработной плате или доходе на душу населения в несколько и даже в десятки раз воспринимаются как вполне естественные, то различия роста людей хотя бы в полтора раза уже воспринимаются как очень сильные

18 Виды дисперсии. Правило сложения дисперсии. Понятие эмпирического коэффициента детерминации и эмпирического корреляционного отношения.

Вариация признака определяется различными факторами, в результате чего различают общую дисперсию, межгрупповую дисперсию и внутригрупповую дисперсию.

Общая дисперсия (σ2) измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию.

Вместе с тем, благодаря методу группировок можно выделить и измерить вариацию, обусловленную группировочным признаком, и вариацию, возникающую под влиянием неучтенных факторов.

Межгрупповая дисперсия (σ2м.гр) характеризует систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под влиянием признака – фактора, положенного в основание группировки, и рассчитывается по формуле

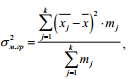
где k – количество групп, на которые разбита вся совокупность;

mj– количество объектов, наблюдений, включенных в группу j;

xj – среднее значение признака по группе j;

x – общее среднее значение признака.

Внутригрупповая дисперсия (σ2j,вн.гр) отражает случайную вариацию, т.е. часть вариации, возникающую под влиянием неучтенных факторов и независящую от признака - фактора, положенного в основание группировки, и рассчитывается по формуле

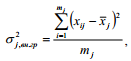
или, на основе метода разностей, по формуле

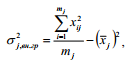
где xij – значение i-ой варианты в группе j.

Если в сформированных группах отдельные данные встречаются не один раз, то для расчета внутригрупповой дисперсии используется формула средней арифметической взвешенной. Среднее значение внутригрупповых дисперсий рассчитывается по формуле

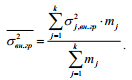
Существует закон, согласно которому общая дисперсия, возникающая под воздействием всех факторов, равна сумме дисперсии, возникающей за счет группировочного признака и дисперсии, появляющейся под влиянием всех прочих факторов.

Правило сложения дисперсий выражается формулой

Правило сложения дисперсии широко применяется при исчислении тесноты связей между признаками (факторным и результативным). Для этого определяют эмпирический коэффициент детерминации и эмпирическое корреляционное отношение. Эмпирический коэффициент детерминации показывает, какая доля всей вариации признака обусловлена признаком, положенным в основание группировки. Эмпирический коэффициент детерминации (η2)рассчитывается по формуле

Эмпирическое корреляционное отношение показывает тесноту связи между признаками группировочным и результативным. Эмпирическое корреляционное отношение (η) рассчитывается по формуле

Оно изменяется в пределах от 0 до 1. Характеристика связи между признаками при соответствующих значениях эмпирического корреляционного отношения приведена в таблице

19 Показатели дифференциации распределения.

Структуру вариационного ряда характеризуют значения признака, аналогичные медиане, которые называются квантилями или градиентами. Квантили (градиенты) – это значения признака, которые делят все единицы ряда распределения на равные по численности группы.

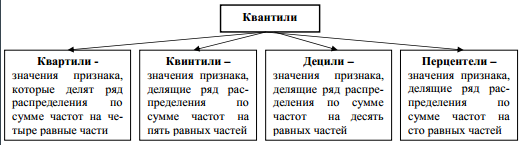
Квантили используются для характеристики степени различия значений уровней признака единиц вариационного ряда. На основании значений квантилей рассчитывают коэффициенты дифференциации: квартильный коэффициент, децильный коэффициент, коэффициент фондов, широко используемые при изучении дифференциации доходов населения.

Для расчета квартильного и децильного коэффициентов рассчитываются соответственно первые и последние квартили и децили.

Отметим, что второй квартиль (Q2)равен медиане, а первый (Q1) и третий (Q3) квартили исчисляются аналогично расчету медианы, только вместо медианного интервала берется для первого квартиля интервал, в котором находится варианта, отсекающая ¼ численности частот, а для третьего квартиля – варианта, отсекающая ¾ частот.

Первый квартиль (Q1) рассчитывается по формуле

третий квартиль (Q3) рассчитывается по формуле

где Xq1 – нижняя граница интервала, содержащего нижний квартиль (интервал определяется

по накопленной частоте, первой превышающей 25 %);

Xq3 – нижняя граница интервала, содержащего верхний квартиль (интервал определяется

по накопленной частоте, первой превышающей 75 %);

Iq– величина интервала (квартильного);

Sq1-1 – накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль;

Sq3-1 – накопленная частота интервала, предшествующего интервалу, содержащему верхний квартиль;

Fq1– частота интервала, содержащего нижний квартиль;

Fq3– частота интервала, содержащего верхний квартиль

20 Показатели концентрации распределения.

К показателям дифференциации близки по значению показатели концентрации: коэффициент концентрации Джини, коэффициент Герфиндаля, коэффициент Розенблюта и др.

Коэффициент концентрации Джини (G) используют для характеристики степени неравномерности распределения значений признака вариационного ряда и рассчитывают по формуле

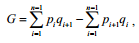
где pi – накопленная частость (доля) численности единиц совокупности;

qi – накопленная доля значений признака i-ой группы, приходящихся на все единицы совокупности. Доля значений признака i-ой группы (di) рассчитывается по формуле

n - число групп в совокупности

Коэффициент концентрации Джини может принимать значения от 0 до 1, поэтому результат следует разделить либо на 100, если pi или qi выражены в процентах, либо на 10000, если оба показателя выражены в процентах.

Удаление значения коэффициента Джини от нуля свидетельствует о возрастании степени неравномерности распределения значений признака в вариационном ряду и концентрации значений признака в отдельных группах.

Коэффициент Герфиндаля (H) рассчитывается по формуле

Группами с незначительной долей значений признака можно пренебречь, так как, будучи озведенной в квадрат, такая доля выражается незначащим числом. Таким образом, значение коэффициента Герфиндаля определяется влиянием лишь доминирующих групп. Механизм расчета коэффициента Герфиндаля позволяет выделить доминирующие в совокупности группы как наиболее весомые составляющие значения Н.

Основное достоинство коэффициента Герфиндаля – его высокая чувствительность к изменению в совокупном объеме долей наиболее крупных единиц совокупности, что позволяет отслеживать концентрацию значений признака. Другое достоинство данного коэффициента заключается в том, что он реагирует на число единиц в группе. Однако ее наибольшим значениям придается наибольший вес. Вследствие этого существует опасность преувеличения уровня концентрации. Поэтому наряду с коэффициентом Герфиндаля целесообразно применять коэффициент Розенблюта, который также характеризует концентрацию, однако расставляет акценты в обратном порядке: наибольший вес придается группам с наименьшими долями.

Коэффициент Розенблюта (KR) рассчитывается по формуле

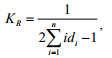
где i – номер группы в совокупности;

di – доля i-ой группы в общем объеме совокупности;

n - число групп в совокупности.

Диапазон значений коэффициента Розенблюта 0 ≤ Kr≤ 1. При n = 1 и d1= 1 Kr= 1. В целом коэффициент Розенблюта имеет тенденцию преуменьшать концентрацию в совокупности.

21 Понятие о закономерностях распределения.

Между изменением значений варьирующего признака и их частотами существует определенная зависимость. Как правило, частоты в вариационных рядах с ростом значения варьирующего признака первоначально увеличиваются, а затем после достижения какой-то максимальной величины в середине ряда уменьшаются (см. табл. 4.7 и 5.3). Значит, частоты в этих рядах изменяются закономерно в связи с изменением варьирующего признака.

Анализ вариационных рядов предполагает выявление закономерностей распределения, определение и построение (получение) некой теоретической (вероятностной) формы аспределения.

Графическое изображение вариационного ряда принимает вид плавной кривой, именуемой кривой распределения.

Примером фактической кривой распределения является полигон распределения, поскольку в нем отражаются как общие, так и случайные условия, определяющие распределение.

Из математической статистики известно, что при увеличении объема статистической совокупности (Ν → ∞) и одновременном уменьшении интервала группировки (h → 0) полигон либо гистограмма распределения все более и более приближаются к некоторой плавной кривой, являющейся для указанных графиков пределом. Эта кривая называется эмпирической кривой распределения и представляет собой графическое изображение в виде непрерывной линии изменения частот, функционально связанного с изменением вариант.

Эмпирические кривые распределения, построенные на основе, как правило, относительно небольшого числа наблюдений (т.е. фактические кривые распределения), очень трудно описать аналитически. Поэтому для выявления статистических закономерностей, сравнения и обобщения различных совокупностей аналогичных данных используются теоретические распределения.

Теоретические распределения – это хорошо изученные в теории распределения, представляющие собой зависимости между плотностями распределения и значениями признака, отражающие закономерности распределения. Они описываются статистическими функциями, параметры которых вычисляются по статистическим характеристикам изучаемой совокупности.

Теоретической кривой распределения называется такая кривая распределения, которая выражает общую закономерность данного типа распределения в чистом виде, исключающем влияние случайных для данного типа закономерностей факторов.

Исследование формы распределения предполагает замену эмпирического распределения известным теоретическим, близким ему по форме. При этом необходимо соблюдать условие: различия между эмпирическим и теоретическим распределением должны быть минимальными. Это означает, что сумма частот эмпирического распределения должна соответствовать сумме частот теоретического распределения. Теоретическое распределение в этом случае является некоторой идеализированной моделью эмпирического распределения, и анализ вариационного ряда сводится к сопоставлению эмпирического и теоретического распределений и определению различий между ними.

В статистической практике наиболее широко используют следующие теоретические распределения:

- биномиальное распределение – для описания распределения дискретного альтернативного признака. Оно представляет собой распределение вероятности исходов события, которые можно оценить как положительные или отрицательные;

- распределение Пуассона – для изучения маловероятных событий в большой серии независимых испытаний (объем совокупностей N ≥ 100, доля единиц, обладающих данным признаком d ≤ 0). Распределение Пуассона обычно применяется в статистическом контроле качества в массовом производстве. Например, при изучении количества бракованных деталей в массовом производстве, числа отказов автоматических линий и т.п.;

- распределение Максвелла применяется при исследовании признака, для которого заранее известно, что распределение имеет положительную асимметрию. Чаще всего распределение Максвелла используется при описании технологических характеристик производственных процесcов

- распределение Стьюдента применяют для описания распределения ошибок в малых выборках (n < 30). Распределение Стьюдента используется только при оценке ошибок выборок, взятых из генеральной совокупности с нормальным распределением признака;

- нормальноераспределение (распределение Гаусса) применяется для описания распределения признаков, на которые действует множество независимых факторов, среди которых нет доминирующих.

22 Показатели формы распределения.

При сравнении эмпирического распределения с нормальным важно констатировать не только согласие этих распределений, но и характер их расхождения. Этому служат показатели формы распределения: показатели асимметрии и эксцесса распределения.

Как отмечалось, нормальное распределение характеризуется симметричностью по отношению к точке, соответствующей значению средней арифметической. Ее вершина находится точно в середине кривой. Поэтому сравнение эмпирического распределения с нормальным, прежде всего, констатирует отсутствие или наличие в нем асимметрии распределения. Асимметричные распределения встречаются чаще, чем симметричные. В асимметричном распределении вершины кривой находятся не в середине, а сдвинуты либо влево, либо вправо. Если вершина сдвинута влево, и, следовательно, правая часть кривой оказывается длиннее левой, то такая асимметрия называется правосторонней. Левосторонней будет асимметрия, когда левая часть кривой длиннее правой, и вершина сдвинута вправо.

Для характеристики асимметрии используют коэффициенты асимметрии.

Коэффициент асимметрии Пирсона (AsП) рассчитывается по формуле

Центральным моментом в статистике называется среднее отклонение индивидуальных значений признака от его среднеарифметической величины. Средние значения разных степеней отклонений индивидуальных значений признака от его средней арифметической величины получили название центральных моментов распределения порядка, соответствующего степени, в которую возводятся отклонения.

Эксцесс распределения (Ех) рассчитывается по формуле

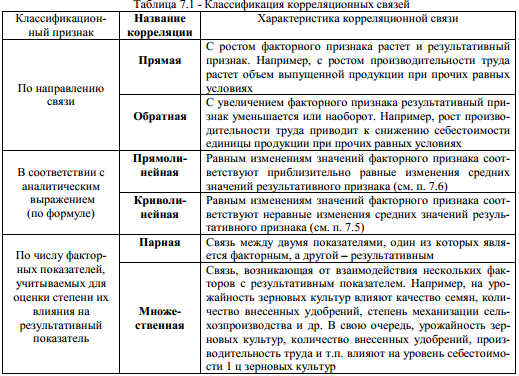
23 Понятие и общая характеристика корреляционных связей

Все явления общественной жизни существуют не изолированно, они органично связаны между собой, зависят друг от друга, обусловливают одно другое и находятся в постоянном движе нии и развитии. Раскрывая взаимосвязи и взаимозависимости между явлениями, можно познать их суть и законы развития.

Причинная зависимость является основной формой закономерных связей, действующих в определенных условиях места и времени. Поэтому, для появления следствия необходимы и причины, и условия, т. е. соответствующие факторы.

Общественные явления или отдельные их признаки, которые влияют на другие и обусловливают их изменение, называются факторными, а общественные явления или отдельные их признаки, которые изменяются под влиянием факторных, называются результативными.

По характеру зависимости явлений различают функциональные (жестко детерминированные) и статистические (или стохастически детерминированные) связи.

Функциональной называется связь, при которой определенному значению факторного признака всегда соответствует, как правило, одно значение результативного признака. Функциональные связи характеризуются полным соответствием между причиной и следствием. Вследствие этого функциональная зависимость всегда выражается точною математической формулой. При этом не обязательно, чтобы одному результативному признаку строго соответствовал только один факторный признак, как, например, в случае связи между длиной окружности и радиусом описываемой формулой: l = 2πR. Существуют функциональные связи, при которых результативный признак является функцией нескольких факторных признаков. Например, площадь земельного участка будет зависеть от длин его сторон: S = a∙b. Функциональные зависимости изучаются точными науками, такими как математика, физика, химия и др. Они очень редко используются для исследования общественных явлений.

Статистическая связь не имеет ограничений и условий, присущих функциональной связи. Связь является статистической, если с изменением значения факторного признака результативный признак может в определенных пределах принимать любые значения с некоторыми вероятностями, но его среднее значение или иные статистические характеристики (показатели вариации, асимметрии, эксцесса и т. п.) изменяются по определенному закону.

Важнейшим частным случаем статистической связи является корреляционная связь. Слово «корреляция» (от английского correlation) означает соотношение, соответствие. Оно удачно отражает особенность зависимости, при которой определенному значению одного факторного признака может соответствовать несколько значений результативного признака, на основе которых можно определить среднюю величину результативного признака, соответствующую каждому конкретному значению факторного признака.

Связь, при которой разным значениям факторного признака соответствуют различные средние значения результативного признака, называется корреляционной связью. Именно корреляционные зависимости наиболее часто используются при исследовании общественных явлений.

Суть корреляционной зависимости сводится к тому, что, с изменением значения факторного признака х закономерным образом изменяется среднее значение результативного признака у, в то время как в каждом отдельном случае значение результативного признака у (с различными вероятностями) может принимать множество различных значений.

Корреляционная связь между признаками может возникать разными путями:

- во-первых, как причинная зависимость результативного признака (его вариации) от вариации факторного признака. Например, зависимость заработной платой работников от стажа их работы, себестоимости продукции от производительности труда, урожайности зерновых от внесения удобрений и т.п.;

- во-вторых, как связь между двумя следствиями общей причины. Классический пример такого рода корреляционной связи приведен А. Чупровым, крупнейшим российским статистиком ХХ в.: прямая зависимость между убытками от пожара и числом пожарных команд в городе определена общей причиной их количества – размером города;

- в-третьих, как взаимосвязь признаков, каждый из которых и причина, и следствие. Такова, например, корреляция между уровнями производительности труда рабочих и уровнем оплаты 1 ч труда (часовой тарифной ставкой).

24 Метод сравнения параллельных рядов

Суть метода сравнения параллельных рядов состоит в том, что полученные в результате группировки и счетной обработки материалы статистического наблюдения располагаются ранжированными по факторному признаку параллельными рядами. Параллельно записываются значения езультативного признака. Это дает возможность, сравнивая значения факторных и результативных показателей, проследить их соотношение, выявить наличие связи и ее направление.

Коэффициент Фехнера оценивает силу связи на основе сравнения знаков отклонений значений вариант от их среднего значения по каждому признаку. Совпадение знаков по факторному и результативному признакам означает согласованную вариацию, несовпадение – нарушение согласованности между признаками.

Коэффициент Фехнера (КФ) рассчитывается по формуле:

Более точно оценивает силу связи коэффициент корреляции рангов. Ранги – это порядковые номера единиц совокупности в ранжированном ряду.

Коэффициент корреляции рангов учитывает согласованность рангов, соответствующих отдельным единицам совокупности по каждому из двух исследуемых признаков.

Совокупность ранжируется по факторному признаку в порядке возрастания и единицам совокупности присваиваются соответствующие ранги. Параллельно проставляются ранги тех же

единиц совокупности, какие они заняли бы в ранжированном ряду по результативному признаку. Коэффициент корреляции рангов (ρ), предложенный американским ученым К. Спирменом, рассчитывается по формуле

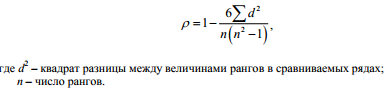
Существует правило, касающееся повторяющихся вариант, ранг которых определяется как средняя арифметическая соответствующих рангов, например, ранг одинаковых величин, занимающих 4 и 5 место, равняется 4,5, т.е. одинаковым по порядку четвертому и пятому значениям признака будут присвоены одинаковые ранги 4,5.

В таком случае коэффициент корреляции рангов Спирмена вычисляется по формуле

25 Метод аналитической группировки. Понятие таблиц взаимной сопряженности

Наличие зависимости между показателями, характеризующими статистическую совокупность, можно выявить с помощью аналитической группировки. Напомним, что статистические группировки, при помощи которых выявляют взаимосвязи между признаками общественных явлений, называются аналитическими.

Метод аналитических группировок как способ выявления корреляционной зависимости между показателями относится к числу наиболее важных методов исследования взаимосвязей.

Результаты группировки единиц совокупности оформляются в виде таблицы, в которой приводится комбинационное распределение единиц совокупности по двум признакам. Такие таблицы называют таблицами взаимной сопряженности. Примером таблицы взаимной сопряженности можно рассматривать таблицу 5.11, в которой приведена группировка сельскохозяйственных предприятий с разной урожайностью зерновых культур по организационно-правовой форме.

Если в таблице оба признака, по которым дано распределение единиц совокупности, количественные, то такая таблица взаимной сопряженности называется корреляционной.

Корреляционная таблица строится по типу «шахматной», т.е. в подлежащем таблицы выделяются группы по факторному признаку х, в сказуемом – по результативному у или наоборот, а в клетках таблицы на пересечении х и у показано число случаев совпадения каждого значения х с соответствующим значением у. Отметим, что для выявления зависимости между непрерывными количественными признаками в сформированных группах по факторному и результативному признакам в качестве х и у принимаются середины соответствующих интервалов

Эмпирическое корреляционное отношение рассчитывается по формуле

Межгрупповая дисперсия результативного признака рассчитывается по формуле

Общая дисперсия результативного признака рассчитывается по формуле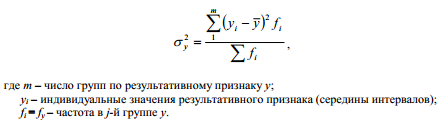

26 Показатели тесноты связи между двумя атрибутивными признаками

Построение таблиц, в которых дается комбинационное распределение единиц совокупности по двум признакам применимо и к атрибутивным признакам. Взаимосвязи между атрибутивными признаками, их влияние на другие показатели, в том числе и количественные, особенно часто приходится изучать при проведении различных социологических исследований.

Простейшей формой таблицы взаимной сопряженности двух атрибутивных признаков является таблица «четырех полей» (четырехклеточная). В ней по каждому признаку выделяются только две группы, чаще всего по альтернативному принципу («да»-«нет», «хорошо»-«плохо» и т.д.).

Для измерения тесноты связи между двумя атрибутивными признаками, имеющими альтернативное выражение, используется коэффициент ассоциации, рассчитываемый с помощью таблицы взаимной сопряженности, которая состоит из четырех клеток, обозначенных латинскими буквами a, b, c, d. Каждая клетка таблицы соответствует определенной альтернативе того или иного признака.

Его существенный недостаток состоит в том, что если в одной из четырех клеток отсутствует частота (т.е. равна 0), коэффициент ассоциации всегда будет равен по модулю 1, и тем самым будет преувеличена мера действительной связи. Чтобы этого избежать, предложен другой показатель – коэффициент контингенции.

Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается достаточно значительной и подтвержденной, если |Касс| > 0,5 или |Кконт| >0,3. Для исследования корреляции атрибутивных альтернативных признаков предложен также коэффициент колигации.

Коэффициент колигации, как и коэффициент контингенции, оценивает связь между признаками более сдержанно, чем коэффициент ассоциации, причем всегда: Касс> Ккол> Кконт.

где φ2 – показатель средней квадратической сопряженности, определяемый путем вычитания единицы из суммы отношений квадратов частот каждой клетки корреляционной таблицы к произведению частот соответствующего столбца и строки, рассчитывается по формуле.

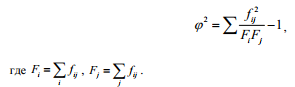
Результат оценки тесноты связи, полученный по коэффициенту взаимной сопряженности Чупрова, более точен, поскольку он учитывает количество групп по каждому из исследуемых признаков. Его выгодно использовать и при большем разделении единиц совокупности на группы по взаимосвязанным признакам. Коэффициент взаимной сопряженности Пирсона используется в основном в случае квадратной таблицы, тогда как Чупрова – пригоден для измерения связи и в прямоугольных таблицах. Считается, что уже при значении коэффициентов взаимной сопряженности 0,3 можно говорить о тесной связи между вариацией исследуемых признаков.

27 Понятие корреляционно-регрессионного анализа

Убедившись при помощи аналитической группировки и расчета показателя эмпирического корреляционного отношения, что теснота связи между исследуемыми явлениями достаточно высока, можно и перейти к корреляционно – регрессионному анализу.

Как уже отмечалось, экономические явления и процессы хозяйственной деятельности предприятий зависят от большого количества взаимодействующих и взаимообусловленных факторов.

В наиболее общем виде задача изучения взаимосвязей факторов состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие. Для ее решения применяются две группы методов, одна из которых включает в себя методы корреляционного анализа, а другая – методы регрессионного анализа, объединенные в методы корреляционно-регрессионного анализа, что имеет под собой некоторые основания: наличие целого ряда общих вычислительных процедур, взаимодополнение при интерпретации результатов и др.

Задачи собственно корреляционного анализа сводятся к измерению тесноты связи между варьирующими признаками и оценке факторов, оказывающих наибольшее влияние на результативный признак. К показателям, используемым для оценки тесноты связи, относятся импирическое корреляционное отношения, теоретическое корреляционное отношение, линейный коэффициент корреляции и т.п.

Задачи регрессионного анализа лежат в сфере установления формы зависимости между исследуемыми показателями, определения функции регрессии, использования уравнения для оценки неизвестных значений зависимой переменной. Найти уравнение регрессии – значит по эмпирическим (фактическим) данным описать изменения взаимно коррелируемых величин.

Уравнение регрессии должно определить, каким будет среднее значение результативного признака у при том или ином значении факторного признака х, если остальные факторы, влияющие на у и не связанные с х не учитывать, т.е. абстрагироваться от них. Уравнение регрессии называют теоретической линией регрессии, а рассчитанные по нему значения результативного признака - теоретическими.

Обычно зависимость, выраженную уравнением прямой, называют линейной (или прямолинейной), а все остальные – криволинейными. Кроме того, различают парную и множественную (многофакторную) корреляцию а, следовательно, и, парную и множественную регрессии.

Корреляционно-регрессионный анализ, в частности многофакторный корреляционный анализ, состоит из нескольких этапов.

На первом этапе определяются факторы, оказывающие воздействие на изучаемый показатель, и отбираются наиболее существенные. От того, насколько правильно сделан отбор факторов, зависит точность выводов по итогам анализа.

На втором этапе собирается и оценивается исходная информация, необходимая для корреляционного анализа. Собранная исходная информация должна быть проверена на точность (достоверность), однородность и соответствие закону нормального распределения. Критерием однородности информации служит среднеквадратическое отклонение и коэффициент вариации. Если вариация выше 33%, то это говорит о неоднородности информации и ее необходимо исключить или отбросить нетипичные наблюдения.

На третьем этапе изучается характер и моделируется связь между факторами и результативным показателем, т.е. подбирается и обосновывается математическое уравнение, которое наиболее точно выражает сущность исследуемой зависимости. Для обоснования функции используются те же приемы, что и для установления наличия связи: аналитические группировки, линейные графи ки и др.

На четвертом этапе проводится расчет основных показателей связи корреляционного анализа. Рассчитываются матрицы парных и частных коэффициентов корреляции уравнения множественной регрессии, а также показатели, с помощью которых оценивается надежность коэффициентов корреляции и уравнения связи: критерий Стьюдента, критерий Фишера, множественные коэффициенты корреляции и др

На пятом этапе дается статистическая оценка результатов корреляционного анализа и практическое их применение. Для этого дается оценка коэффициентов регрессии, коэффициентов эластичности и бета-коэффициентов.

Одним из основных условий применения и ограничения корреляционно-регрессионного метода является наличие данных по достаточно большой совокупности явлений. Обычно считают, что число наблюдений должно быть не менее чем в 5-6, а лучше – не менее чем в 10 раз больше числа факторов.

32.Сравнительный анализ рядов динамики.

Для оценки интенсивности изменения уровней показателей взаимосвязанных рядов динамики проводят их сравнительный анализ. Под взаимосвязанными рядами динамики понимают такие, в которых уровни одного ряда в какой-то степени определяют уровни другого. Например: ряд, отражающий внесение удобрений на 1 га, связан с временным рядом урожайности; ряд средней выработки связан с рядом динамики заработной платы работников и т. д.

В простейших случаях для характеристики взаимосвязи двух и более рядов их приводят к общему основанию, для чего берут в качестве базисных уровни за один и тот же период, как правило, начальный в ряду динамики, и исчисляют коэффициенты опережения по темпам роста иприроста.

Коэффициенты опережения по темпам роста ( опер поТ р К . ) представляют собой отношение темпов роста (цепных или базисных) одного ряда ( 1 р Т ) к соответствующим по времени темпам ро-

ста (также цепным или базисным) другого ряда ( 2 р Т ) и рассчитывается по формуле

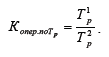
Аналогично находятся и коэффициенты опережения по темпам прироста.

33.Структура ряда динамики.

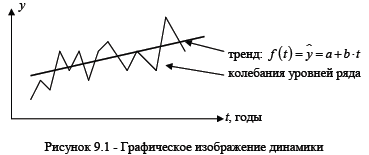
Уровни ряда динамики формируются под совокупным влиянием множества олговременных и краткосрочных факторов, и, в том числе, различного рода случайных обстоятельств. В связи с чем, при статистическом изучении динамики необходимо четко разделить ее на два основных элемента – тенденцию и колеблемость.

Тенденция развития динамического ряда к увеличению либо снижению его уровней - основная закономерность изменения уровней ряда. В отдельные же годы уровни испытывают колебания, отклоняясь от основной тенденции.

Тенденция динамики связана с действием долговременно существующих причин и условий развития, хотя, конечно, после какого-то периода эти причины и условия тоже могут измениться и породить уже другую тенденцию развития изучаемого объекта. Основная тенденция развития динамического ряда выражается в форме уравнения, называемого трендом. Колебания же, напротив, связаны с действием краткосрочных или циклических (конъюнк-турных) факторов, влияющих на отдельные уровни динамического ряда, и отклоняющих уровни от тенденции то в одном, то в другом направлении. Например, тенденция динамики урожайности связана с прогрессом агротехники, с укреплением экономики данной совокупности хозяйств, совершенствованием организации производства. Колеблемость урожайности вызвана чередованием

благоприятных по погоде и неблагоприятных лет, циклами солнечной активности, колебаниями в развитии вредных насекомых и болезней растений.

Тенденцию и колебания наглядно показывает график (рис. 9.1). По оси абсцисс на графике всегда отражается время, по оси ординат – уровни. По обеим осям строго соблюдается масштаб, иначе характер динамики будет искажен.

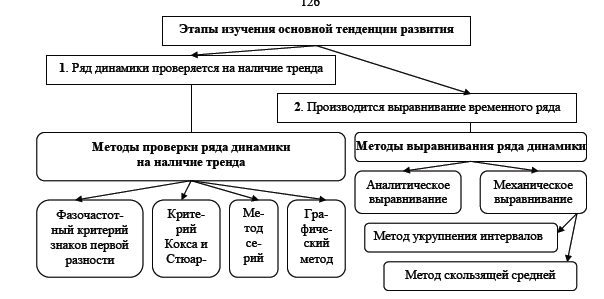
34.Изучение основной тенденции развития.

Изучение основной тенденции развития осуществляется в два этапа (рис. 9.2):

- на первом этапе ряд динамики проверяется на наличие тренда;

- на втором этапе проводится выравнивание временного ряда и непосредственное выделение тренда с экстраполяцией полученных результатов.

Проверка на наличие тренда в ряду динамики может быть осуществлена различными методами, в частности, приведенными на рис. 9.2

Суть фазочастотного критерия знаков первой разности (Валлиса и Мура) заключается в

том, что наличие тренда в динамической ряду утверждается в том случае, если этот ряд не содержит либо содержит в приемлемом количестве фазы - изменения знака разности первого порядка (абсолютного цепного прироста).

Суть критерия Кокса и Стюарта сводится к тому, что весь анализируемый ряд динамики

разбивается на три равные по числу уровней группы (если количество уровней ряда динамики не делится на три, недостающие уровни нужно добавить) и сравнивают между собой, например, сумарные

или средние уровни первой и последней групп. Существенное различие между ними позволяет сделать вывод о наличии тренда.

В соответствии с методом серий каждый конкретный уровень временного ряда считается

принадлежащим к одному из двух типов: например, если, уровень ряда меньше медианного значения, то считается, что он имеет тип А, в противном случае - тип В. После замены числовых значений уровней ряда буквами А и В последовательность уровней временного ряда выступает как последовательность типов. В образовавшейся последовательности типов определяется число серий (R). Серией называется любая последовательность элементов одинакового типа, граничащая с элементами другого типа. Если во временном ряду общая тенденция к росту или снижению отсутствует, то количество серий является случайной величиной (для n >10) и оказывается в доверительном интервале, характеризуемом неравенством:

где R - среднее число серий, определяемое по формуле

n - число уровней ряда;

t – нормированное отклонение - параметр, назначаемый в соответствии с принятым

уровнем доверительной вероятности Значения t даются в таблицах нормального

распределения вероятностей. Наиболее часто используемые сочетания t и Р приведены в таблице;

QR - среднее квадратическое отклонение числа серий, которое рассчитывается по формуле

35 Аналитическое выравнивание рядов динамики

Под аналитическим выравниванием понимают определение основной проявляющейся во времени тенденции развития изучаемого явления, выраженной соответствующим уравнением регрессии. При этом развитие предстает как бы в зависимости только от течения времени, т.е. одного фактора - времени. В итоге выравнивания временного ряда получают наиболее общий, суммарный, проявляющий во времени результат действия всех причинных факторов. Отклонение конкретных уровней ряда от уровней, соответствующих общей тенденции, объясняют действием факторов, проявляющихся случайно или циклически.

На практике по имеющемуся временному ряду задают вид и находят параметры функции f(t), а затем анализируют поведение отклонений от тенденции.

Функцию f(t) выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса. Чаще всего при выравнивании используются следующие зависимости:

- линейная, выраженная уравнением

- параболическая, выраженная уравнением

- экспоненциальная, выраженная уравнением

Выравнивать динамические ряды по уравнению прямой линии целесообразно тогда, когда более или менее постоянны цепные абсолютные приросты, т.е. тогда, когда уровни ряда изменяются приблизительно в арифметической прогрессии.

Выравнивание динамических рядов по уравнению квадратической параболы необходимо применять в тех случаях, когда изменение уровней ряда происходит с приблизительно равномерным ускорением или замедлением цепных абсолютных приростов.

Выравнивание по экспоненциальной функции целесообразно использовать тогда, когда уровни ряда динамики выявляют тенденцию постоянства цепных темпов роста, т.е. в случае изменения уровней ряда динамики в геометрической прогрессии.

Кроме выше рассмотренных существуют логарифмическая, гиперболическая, логистическая и др. формы тренда.

Для расчета параметров уравнения тренда обычно используют метод наименьших квадратов. Для каждого типа тренда МНК дает систему нормальных уравнений, решая которую вычисляют параметры тренда.

36 Характеристика колеблемости

При изучении и измерении тенденции динамики колебания уровней играли лишь роль помех, «информационного шума», от которого следовало по возможности абстрагироваться. Однако факторы, обусловливающие колебания уровней временного ряда, как правило, объективны, что предопределяет самостоятельное исследование колеблемости.

Значение изучения колебаний уровней динамического ряда определяется, в первую очередь, тем, что регулирование рыночной экономики, как со стороны государства, так и производителей в значительной мере состоит в регулировании колебаний экономических процессов. Например, колебания урожайности, продуктивности скота, производства сельхозпродукции экономически нежелательны, так как потребность в продукции агрокомплекса постоянна. Эти колебания следует уменьшать, применяя прогрессивную технологию и другие меры. Напротив, сезонные колебания объемов производства зимней и летней одежды, обуви, мороженного, прохладительных напитков и т.п. – необходимы и закономерны, так как спрос на эти товары тоже колеблется по сезонам и равномерное производство требует лишних затрат на хранение запасов.

Пилообразная или маятниковая колеблемость состоит в попеременных отклонениях уровней ряда от тренда то в одну, то в другую сторону. Такие колебания можно наблюдать в динамике урожайности при невысоком уровне агротехники: высокий урожай при благоприятных условиях погоды выносит из почвы больше питательных веществ, чем их образуется естественным путем за год, следовательно, почва обедняется, что вызывает снижение следующего урожая ниже тренда, который выносит меньше питательных веществ, чем образуется за год и плодородие возрастает, и т.д.

Циклическая долгопериодическая колеблемость свойственна, например, солнечной активности (10-летние циклы), а, значит, и связанным с ней на Земле процессами – урожайности отдельных культур в ряде районов, некоторым заболеваниям людей, растений и т.п. Для этого типа колеблемости характерны редкая смена знаков отклонений от тренда и кумулятивный эффект отклонений одного знака, который может тяжело отражаться на экономике. Зато эти колебания хорошо прогнозируются.

Случайно распределенная во времени колеблемость – нерегулярная, хаотическая. Она может возникнуть при наложении множества колебаний с разными по длительности циклами. Но может возникать и в результате столь же хаотической колеблемости главной причины существования колебаний, например суммы осадков за летний период, температуры воздуха в среднем за месяц в разные годы.

37 Сезонные колебания

Особого внимания при изучении колеблемости заслуживают сезонные колебания. Сезонные колебания строго цикличны – повторяются через каждый год.

Сезоннымиколебаниями называют периодические колебания уровней, возникающие под влиянием смены времени года. Роль сезонных колебаний велика в агропромышленном комплексе, торговле многими товарами, заболеваемости, строительстве, деятельности рекреационных учреждений, на транспорте.

Сезонность наносит большой ущерб народному хозяйству, связанный с неравномерным использованием оборудования и рабочей силы, с неравномерной загрузкой транспорта и т.д.

Для изучения сезонных колебаний необходимо иметь уровни за каждый месяц (квартал) года, а, чтобы сгладить случайные колебания и точнее измерить сезонные, их изучают за несколько лет.

Уровень сезонности и форма «сезонной волны» изучаются с помощью индексов сезонности.

Способы определения индексов сезонности зависят от наличия или отсутствия основной тенденции.

Индивидуальные индексы сезонности показывают, во сколько раз фактический уровень ряда в момент (интервал) времени t больше среднего уровня, соответствующего данному моменту (интервалу) времени, либо уровня, вычисляемого по уравнению тенденции f(t).

Индекс сезонности (t,сезI), если тренда нет или он незначителен, рассчитывают по формуле

49. Статистические таблицы/ Статистическая таблица – это система строк и столбцов, в которых в определенной после довательности и связи излагается статистическая информация о социально-экономических явлениях. Различают подлежащее и сказуемое статистической таблицы.

Подлежащим таблицы называется объект исследования, отдельные единицы или его части

(группы), которые характеризуются соответствующими показателями.

Сказуемым таблицы называются показатели, которые характеризуют подлежащее.

Подлежащее таблицы обычно составляет название ее строк, сказуемое – название граф (ко-

лонок). Иногда в целях получения более компактной таблицы подлежащее и сказуемое меняют

местами, т.е. подлежащее указывают по графам, а сказуемое по строкам. По построению подлежащего таблицы могут быть простыми, групповыми и комбинацион-

ными.

Простой называется такая статистическая таблица, в подлежащем которой нет группировок.

Простые таблицы бывают: 1перечневые 2территориальные 3 хронологические

Как правило, простые таблицы представляют данные в динамике.

Групповой называется таблица, в подлежащем которой изучаемый объект разделен на груп-

пы по какому-либо признаку, например, таблицы 3.5 – 3.7. Такие таблицы, как правило, характе-

ризуют в динамике состав и структуру изучаемого явления.

Комбинационной таблицей называется такая, где в подлежащем дана группировка единиц

совокупности по двум и более признакам, взятым в комбинации, например, таблица 3.10.

Таблицы различаются и по разработке сказуемого, которая может быть простой и сложной.

Основные правила построения таблиц

1. Таблица по возможности должна быть краткой. Не следует загружать ее излишними по-

дробностями, затрудняющими анализ исследуемых явлений.

2. Каждая таблица должна иметь подробное название, из которого становится известно:

а) какой круг вопросов излагает и иллюстрирует таблица;

б) каковы географические границы статистической совокупности, представленные таблицей;

в) каков период времени, за который приведены данные, или момент времени, к которому

они относятся;

г) каковы единицы измерения (если они одинаковы для всех табличных клеток).

3. Если единицы измерения не одинаковы, то в верхних или боковых заголовках обязательно

следует указывать, в каких единицах приводятся статистические данные (т, шт., грн. и пр.).

4. В таблице желательно давать нумерацию граф. Это облегчает пользование таблицей, дает

возможность лучше ориентироваться, показывает способ расчета цифр в графах. Графы боковика

обозначаются заглавными буквами алфавита; графы, содержащие количественные данные, нумеруются арабскими цифрами. Заголовки строк и граф должны быть сформулированы кратко, точно

и ясно. Все слова в заголовках записываются по возможности полностью. Заголовки граф следует

сформулировать так, чтобы были ясны смысл данной величины и порядок ее расчета.

5. Приводимые в подлежащем признаки должны быть расположены в логическом порядке с

учетом необходимости рассматривать их совместно. Обычный принцип размещения – от частного

к общему, т.е. сначала показывают слагаемые, а в конце подводят итоги (если это необходимо).

Когда приводятся не все слагаемые, а лишь наиболее важные из них, применяется противополож-

ный принцип – сначала показывают общие итоги, а затем выделяют наиболее важные части («В

том числе», «Из них»).

6. Следует различать «Итого» и «Всего». «Итого» является итогом для определенной части

совокупности, а «Всего» - итог для совокупности в целом.

7. Таблица может сопровождаться примечаниями, в которых указываются источники дан-

ных, более подробно раскрывается содержание показателей, даются и другие пояснения, а также

оговорки в случае, если таблица содержит данные, полученные в результате вычислений.

8. Все данные одной строки (графы) следует представлять с одинаковой степенью точности.

9. Все клетки таблицы должны быть заполнены.

48. Определение численности выборки Разрабатывая программу выборочного наблюдения, сразу задают величину допустимой

ошибки выборки и доверительную вероятность. Неизвестным остается тот минимальный объем

выборки, который должен обеспечить требуемую точность средней и доли.

Формулы для определения объема (численности) выборки, позволяющего обеспечить требу-

емую точность значений соответствующих показателей, в зависимости от метода отбора для сред-

ней и доли приведены.