38. Общая характеристика статистических индексов

В переводе с латинского языка слово «индекс» означает «показатель», однако в статистике

оно приобретает самостоятельное значение.

Статистический индекс – относительный показатель, отражающий соотношение величин

сложного экономического явления, состоящего из соизмеримых или несоизмеримых элементов.

Значительная часть статистических совокупностей, состоит из элементов, которые можно

подытожить. Так, для анализа динамики численности рабочих и служащих, занятых в народном

хозяйстве страны, всего лишь нужно суммировать соответствующие данные по отдельным отрас-

лям народного хозяйства базисного и отчетного периодов. Соотношение численности всех работ-

ников, занятых в народном хозяйстве страны, отчетного и базисного периодов возможно потому,

что в основе таких сравнений лежит соизмеримость элементов, из которых складываются сравни-

ваемые совокупности. Однако большинство совокупностей состоит из элементов, непосредствен-

но не суммируемых. Например, с такими совокупностями имеют дело, когда изучают динамику

производства продукции или объема товарооборота, которые в натуральной форме складываются

из разных потребительских благ и, будучи, выраженными в натурально-вещественной форме, эти

элементы не могут непосредственно суммироваться. Нельзя складывать тонны цемента и тонны

сахара, или пары обуви и м3 газа и т.д.

Чтобы преодолеть существующую несоизмеримость элементов сложного явления использу-

ют соизмеритель, в основе которого лежит то общее, что свойственно всем элементам совокупно-

сти независимо от их натурально-вещественной формы. Например, это может быть стоимость

продукта, выражаемая ценой. Стоимость разнородной продукции можно складывать, определяя

тем самым объем всей продукции, что позволяет рассчитывать обобщающие показатели в виде

индексов. Посредством денежного выражения стоимости отдельных видов продукции исчезает

(снимается) их несравнимость как потребительных стоимостей.

С помощью индексного метода решаются следующие задачи: 1получают сравнительную характеристику изменения явления во времени, где индексы выступают как показатели динамики

2- характеризуют выполнение установленной нормы, утвержденного стан-

дарта (плана), где индексы выступают как показатели выполнения зада-

ния (плана) и являются средством оперативного отражения хода производ-

ственного процесса. 3. дают сравнительную характеристику изменения явления в пространстве,

в этом случае индексы обеспечивают территориальное сравнение (терри-

ториальные индексы) 4. оценивают роль отдельных факторов, формирующих сложное явлениеНапомним, что количественные показатели представлены абсолютными величинами, харак-

теризующими объем или уровень развития явления, которые выражаются в определенных (как

правило, натуральных, трудовых, демографических) единицах измерения. Качественные показате-

ли, выражены, как правило, относительными величинами интенсивности (см. тему 4), и характе-

ризуют уровень изучаемого результативного показателя в расчете на количественную единицу и

определяются как отношение данного результативного показателя к связанному с ним количе-

ственному показателю, на единицу которого он рассчитывается. Например, себестоимость едини-

цы продукции рассчитывается как отношение суммарных затрат на производство к количеству

продукции.

50. Общая характеристика и элементы статистических графиков

Графики являются самой эффективной формой представления данных с точки зрения их восприятия. С помощью графиков достигается наглядность характеристики структуры, динамики, взаимосвязи явлений, их сравнения. Они позволяют легко выявить и наглядно представить закономерности, которые часто трудно бывает уловить в сложных статистических таблицах. На графике сразу видны пределы изменения показателя, сравнительная скорость изменения разных показателей, их колеблемость. Вместе с тем графики имеют определенные ограничения: прежде всего, график не может включить столько данных, сколько может войти в таблицу; кроме того, на графике показываются всегда округленные данные – не точные, а приблизительные. Статистические графики представляют собой условные изображения числовых величин и их соотношений посредством линий, геометрических фигур, рисунков или географических карт схем. Каждый график состоит из графического образа и вспомогательных элементов. Графический образ – это совокупность точек, линий и фигур, с помощью которых изображаются статистические данные. Эти знаки образуют собственно языковую ткань графика, его основу.

Вспомогательными элементами графика являются:

1) поле графика – то пространство, в котором размещаются образующие график геометрические знаки. Поле графика характеризуется его форматом, т.е. размером и пропорциями (соотношением сторон);

2) пространственные ориентиры, определяющие расположение геометрических знаков в поле графика. Пространственные ориентиры задаются системой координатных сеток или контурных линий, которые делят это поле на части. В большинстве случаев в статистических графиках применяется система прямоугольных (декартовых) координат;

3) масштабные ориентиры, придающие геометрическим знакам количественную определенность. Масштабные ориентиры определяются системой масштабных шкал или специальными масштабными знаками. Масштабные шкалы представляют собой геометрическое место помеченных точек, а носителями их являются оси координат, на которых эти отметки располагаются.

4) экспликация графика, состоящая из объяснения: а) предмета, изображаемого графиком (названия графика); б) смыслового значения каждого знака, применяемого на данном графике.

Без экспликации график нельзя прочитать и понять. Название графика должно кратко и точно раскрывать его содержание. Пояснительные тексты могут располагаться в пределах графического образа или рядом с ним (ярлыки), а также выносить за его пределы (ключ).

51. Классификация статистических графиков

Многообразие видов графиков обусловлено различиями в их статистическом содержании, способах построения и широтой круга изображаемых ими общественных явлений и процессов. По содержанию можно выделить графики сравнения в пространстве, графики различных относительных величин (структуры, динамики и т. п.), графики вариационных рядов (рядов распределения), графики размещения на территории, графики взаимосвязанных показателей. Возможны и комбинации этих графиков, например графическое изображение вариации в динамике или динамики взаимосвязанных показателей и т. п. По способу построения графики можно разделить на диаграммы, картограммы и картодиаграммы. Диаграмма – чертеж, наглядно изображающий соотношение каких-нибудь величин. По характеру графического образа различают точечные, линейные, плоскостные (столбиковые, полосовые (ленточные), квадратные, круговые, секторные) и объемные диаграммы. Линейные (динамические) диаграммы применяют для изображения экономических явлений, протекающих во времени. Геометрическими знаками-символами на таких диаграммах служат точки и последовательно соединяющие их прямые линии, складывающиеся в ломанные «кривые», конфигурация которых дает представление об изображаемом процессе. Ось абсцисс является в такой диаграмме осью времени с равномерно размещенными отметками, а ось ординат – осью значений, которые принимает с течением времени изучаемый показатель. Конфигурация каждой кривой на динамической диаграмме отражает процесс изменения во времени описываемого на диаграмме показателя, а именно: движение кривой с ходом времени вправо и вверх означает рост показателя, а движение ее вправо и вниз – его падение. Столбиковые диаграммы, чаще всего, используют для сравнения одноименных показателей, характеризующих различные объекты или территории. Значения сравниваемых показателей изображается при этом в виде прямоугольных столбиков, имеющих одинаковую ширину и расположенных на общей горизонтальной или вертикальной линии. Высота (или длина) каждого столбика в определенном масштабе соответствует величине изображаемого показателя. Полосовая диаграмма, являющаяся разновидностью столбиковой, особенно удобна в тех случаях, когда отдельные объекты сравнения характеризуются противоположными по знаку показателями. Иногда сравниваемые объекты характеризуются резко разнящимися значениями показателей данные которых представить с помощью столбиковой диаграммы практически невозможно. В подобных случаях используют особые виды плоскостных диаграмм – квадратные и круговые. Их построение основано на том, что величины изображаемых показателей должны быть пропорциональны площадям квадратов или кругов, а корни квадратные из сравниваемых величин – линейным размерам этих фигур (сторонам квадратов или радиусам кругов Другой формой структурных статистических диаграмм являются полосовые диаграммы Картограммы и картодиаграммы являются средством наглядного изображения фактических показателей, характеризующих отдельные географические единицы (районы, области, страны) по тому или иному признаку. На картограмме распределение изучаемого признака по территории изображается условными знаками (точками, штриховкой, цветом и т.д.), соответствующими определенным интервалам значений величины этого признака. Эти знаки покрывают контур каждого района. Картограмма применяется в тех случаях, когда возникает необходимость показать территориальное распределение какого-нибудь одного статистического признака между отдельными районами для выявления закономерностей этого распределения. Картограммы бывают фоновые и точечные. Картодиаграмма – это сочетание диаграммы с географической картой. В качестве изобразительных знаков в картодиаграммах используются те или иные фигуры, которые размещаются на контуре географической карты. При помощи картодиаграммы можно выразить пространственную специфику в структурах изучаемых статистических совокупностей, особенности каждого района как единого целого и т.д. Например, структурная или секторная картодиаграмма, характеризующая порайонные различия в структуре посевных площадей. В качестве диаграммных знаков в картодиаграмме часто используют различные геометрические фигуры, особенно круги, которые наиболее просты и удобны для выражения сравниваемых количественных показателей на карте.

28.Прямая линейная регрессия

Парная линейная зависимость – наиболее часто используемая форма связи между двумя коррелируемыми признаками, выражаемая при парной корреляции уравнением прямой:

Коэффициент регрессии а1 показывает, на сколько (в абсолютном выражении) изменится результативный признак у при изменении факторного признака х на единицу. Если а1 имеет положительный знак, то связь прямая, если отрицательный – связь обратная. Параметры уравнения связи определяются способом (методом) наименьших квадратов (МНК) с помощью составленной и решенной системы двух уравнений с двумя неизвестными:

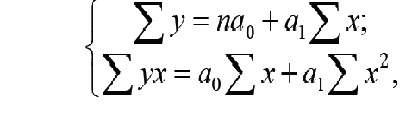
Для справки: суть метода наименьших квадратов заключается в следующем требовании: искомые теоретические значения результативного признака должны быть такими, при которых бы обеспечивалась минимальная сумма квадратов их отклонений от эмпирических значений, т.е.

Решив систему уравнений, получаем значения параметров уравнения связи, определяемые по Формулам

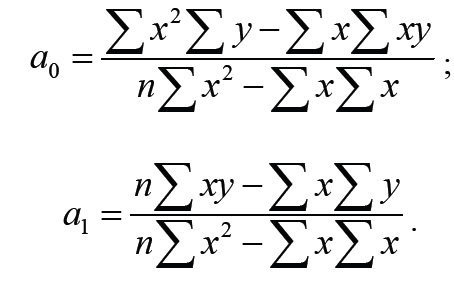Если параметры уравнения определены правильно, то

Для экономической интерпретации линейных и нелинейных связей между двумя исследуемыми явлениями часто используют рассчитанные на основе уравнений регрессии коэффициенты эластичности. Коэффициент эластичности показывает, на сколько процентов изменится в среднем результативный признак у при изменении факторного признака х на 1 %. Для линейной зависимости коэффициент эластичности (ε) определяется:- для отдельной единицы совокупности по формуле

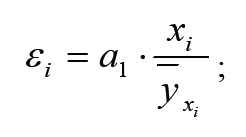- в целом для совокупности по формуле

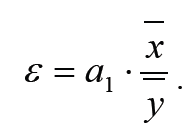Определение тесноты связи в корреляционно-регрессионном анализе основывается на правиле сложения дисперсий, как и в методе аналитической группировки. Но в отличие от него, где для оценки линии регрессии используют групповые средние результативного признака, в корреляционно-регрессионном анализе для этой цели используют теоретические значения результативного признака.

Для определения тесноты связи необходимо рассчитать дисперсию отклонений у и x y , то есть остаточную дисперсию, которая обусловлена влиянием всех факторов, кроме фактора х. Разница между общей и остаточной дисперсиями дает теоретическую (факторную) дисперсию, которая измеряет вариацию, обусловленную фактором х. На сопоставлении этой разницы с общей дисперсией построен индекс корреляции или теоретическое корреляционное отношение (R), которое определяется по формулам

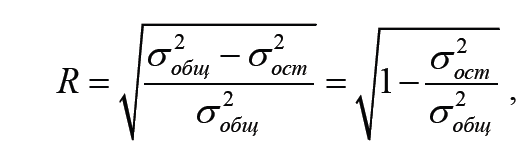Или

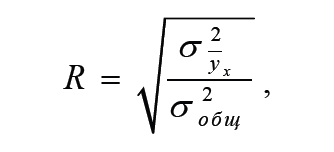
Факторную дисперсию по теоретическим значениям исчисляют по формуле

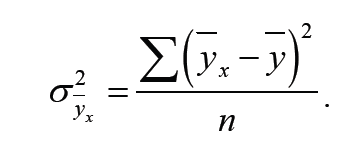Остаточную дисперсию определяют по формулам

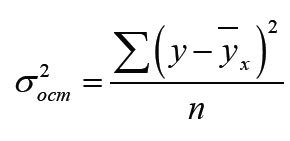Или

Коэффициент детерминации (R2) характеризует ту часть вариации результативного признака у, которая соответствует линейному уравнению регрессии (т.е. обусловлена вариацией факторного признака) и исчисляется по формуле

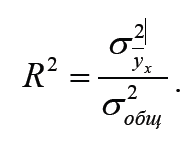Индекс корреляции принимает значения от 0 до 1. Когда R = 0, то связи между вариацией

признаков х и у нет. Остаточная дисперсия равняется общей, а теоретическая дисперсия равняется нулю. Для измерения тесноты связи и определения ее направления при линейной зависимости используется линейный коэффициент корреляции (r), определяемый по формулам

Или

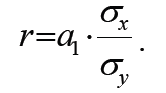Значение r колеблется в пределах от –1 до +1. Положительное значение r означает прямую связь между признаками, а отрицательное – обратную. Проверка надежности (существенности) связи в корреляционно-регрессионном анализе осуществляют при помощи тех же самых критериев и процедур, что и в аналитической группировке. Фактическое значение F-критерия определяют по формуле

Степени свободы k1 и k2 зависят от числа параметров уравнения регрессии (m) и количества единиц исследуемой совокупности (n) и рассчитываются по формулам

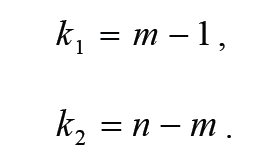Для установления достоверности рассчитанного линейного коэффициента корреляции ис-

пользуют критерий Стьюдента, рассчитываемый по формуле

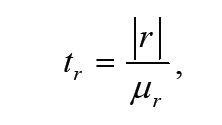
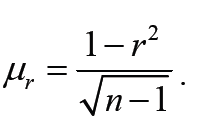При достаточно большом числе наблюдений (n > 50) коэффициент корреляции можно считать достоверным, если он превышает свою ошибку в 3 и больше раз, а если он меньше 3, то связь между исследуемыми признаками у и х не доказана.

29. Понятие многофакторного корреляционно-регрессионного анализа.

на исследуемый результативный показатель каждого из введенных в модель факторов при фиксированных на среднем уровне других факторах. При этом важным условием является отсутствие функциональной связи между факторами. Математически задача корреляционно-регрессионного анализа сводится к поиску аналитического выражения, которое как можно лучше отражало бы связь факторных признаков с результативным признаком, т.е. к нахождению функции:

Наиболее сложной проблемой является выбор формы связи, выражающейся аналитическим уравнением, на основе которого по существующим факторам определяются значения результативного признака – функции. Эта функция должна лучше других отражать реально существующие связи между исследуемым показателем и факторами. Эмпирическое обоснование типа функции при помощи графического анализа связей для многофакторных моделей практически непригодно. Форму связи можно определить путем перебора функций разных типов, но это связано с большим количеством лишних расчетов. Принимая во внимание, что любую функцию нескольких переменных можно путем логарифмирования или замены переменных привести к линейному виду, уравнение множественной регрессии можно выразить в линейной форме:

Параметры уравнения находят методом наименьших квадратов. Для характеристики тесноты связи в множественной линейной корреляции используют множественный коэффициент корреляции ( yx1x2 R ), рассчитываемый по формуле

где

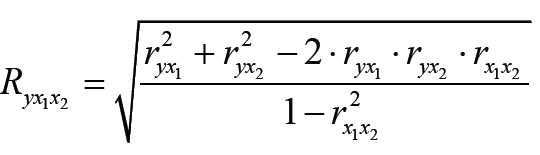
– парные коэффициенты линейной корреляции, позволяющие оценить влияние каждого фактора отдельно на результативный показатель, и определяемые по формулам

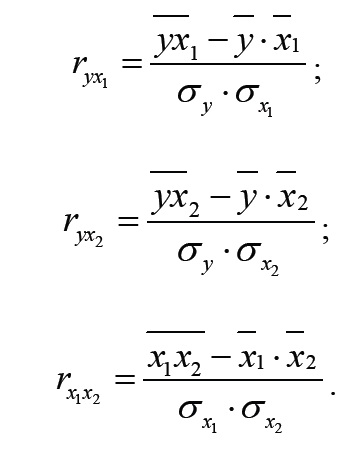Множественный коэффициент корреляции колеблется в пределах от 0 до + 1 и интерпретируется так же как и теоретическое корреляционное отношение. Совокупный коэффициент множественной детерминации показывает, какую часть общей корреляции составляют колебания под влиянием факторов х1, х2, …, хn, положенных в многофакторную модель для исследования. На основе парных коэффициентов корреляции находятся частные коэффициенты корреляции первого порядка, показывающие связь каждого фактора с исследуемым показателем в условиях комплексного взаимодействия факторов, рассчитываемые по формулам

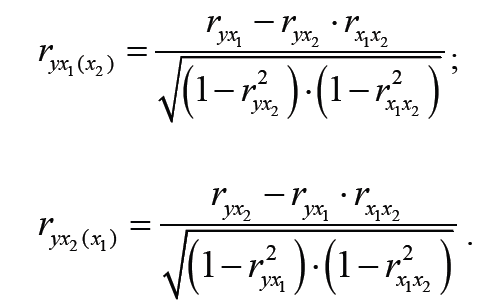
31. Статистические характеристики рядов динамики.

При изучении развития явления во времени оценивается его интенсивность и рассчитываются средние показатели динамики. Для характеристики интенсивности изменения явления во времени рассчитываются показатели абсолютного прироста, коэффициента роста, темпа роста, темпа прироста, абсолютного значения одного процента прироста. В основе расчета этих показателей лежит сравнение определенных уровней ряда с уровнями, принятыми за базу сравнения. Отметим, что уровни показателей, соответствующие определенному i-ому периоду (моменту) времени, обозначаются уi; уровни показателей, соответствующие периоду (моменту) времени, предшествующему i-ому периоду (моменту) времени, - уi-1; уровни показателей, соответствующие периоду (моменту) времени, начальному в ряду динамики, - у0. В случае, когда сравнение проводится с периодом (моментом) времени, начальным в ряду динамики, получают базисные показатели динамики, характеризующие окончательный результат всех изменений в уровнях ряда от периода, к которому относится базисный уровень до конкретного i-го периода. Если же сравнение проводится с предыдущим периодом или моментом времени, то получают цепные показатели динамики, характеризующие интенсивность изменения уровня от периода к периоду (или от даты к дате) в пределах изучаемого промежутка времени.. Абсолютный прирост показывает, на сколько данный уровень ряда превышает уровень, принятый за базу сравнения. Коэффициент роста показывает, во сколько раз данный уровень превышает уровень, принятый за базу сравнения. Темп роста показывает, сколько процентов составляет данный уровень по сравнению с уровнем принятым за базу сравнения. Темп прироста показывает, на сколько процентов определенный уровень ряда больше (меньше) уровня, принятого за базу сравнения. Следует отметить, что базисный абсолютный прирост равен сумме цепных абсолютных приростов в исследуемом периоде, а базисный коэффициент роста равен произведению цепных коэффициентов роста в исследуемом периоде. Зависимость между базисными и цепными показателями динамики характеризуется формулами.

Средний уровень ряда – это показатель, обобщающий итоги развития явления за единичный интервал (момент) из имеющейся временной последовательности. Расчет среднего уровня ряда динамики определяется видом этого ряда и величиной интервала, соответствующего каждому уровню.