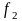- •При прочих равных условиях значение абсолютной величины определяется размером совокупности Виды абсолютных величин
- •Счет производства
- •Способы расчета дисперсии.
- •Расчет способом моментов
- •Классификация рядов динамики
- •Уровни ряда динамики Динамика явления по показателю
- •Методика исчисления среднего уровня ряда динамики
- •Способ моментов в расчете средней величины признака
- •Средние по положению Мода ( ) – вариант ( значение признака ) наибольшей численности (частоты).
- •3. Определение значения медианы:
- •Размах вариации - мерой различия вариантов служить не может. В случае ; ; , вариацию признака представляют:
- •Способы расчета дисперсии.
- •Расчет способом моментов
- •К расчету показателей вариации тарифного разряда
- •К расчету показателей вариации заработной платы работников
- •Виды дисперсии.
- •Сводка статистических данных
- •Виды сводки
- •Сводка состоит из следующих этапов:
- •Понятие и виды группировки
- •Группировка статистических данных
- •Виды группировок
- •Объект статистики страхования.
- •Уровни ряда динамики Динамика явления по показателю
- •Методика исчисления среднего уровня ряда динамики
- •Методика исчисления среднего уровня ряда динамики
- •Методика расчета среднего уровня ряда динамики (продолжение) Моментный ряд абсолютных суммарных величин
- •График состояния явления по показателю
- •Показатели изменения уровня ряда
- •Показатели изменения уровня ряда
- •К определению среднего темпа роста
- •1) Формула агрегатного индекса Пааше:
- •По методу начисления процентов различают:
- •При сроке пользования ссудой менее одного года:
- •2. Общий индекс валовой продукции:
- •3. Общий индекс численности поголовья:
Классификация рядов динамики
Основание классификации |
|
Время |
Показатель (статистическая величина)
|
Интервальный: за равные интервалы; за неравные интервалы (нежелательно).
Моментный: на отчетные моменты; на моменты изменения состояния (случайные) |
Абсолютная суммарная величина
Производная величина (статистический коэффициент): средняя величина; относительная величина
|
Уровни ряда динамики Динамика явления по показателю
Время |
|
|
… |
|
|
|
… |
|
|
Показатель |
|
|
… |
|
|
|
… |
|
|
Здесь - исходное: - начальный уровень, - конечный уровень
в ходе сравнения: - текущий уровень
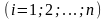 ,
- уровень предшествующий текущему,
-
,
- уровень предшествующий текущему,
-
уровень последующий за текущим
Средний
уровень ряда
 - средняя величина из
уровней ряда динамики является
характеристикой всего периода (интервала)
ряда динамики
- средняя величина из
уровней ряда динамики является
характеристикой всего периода (интервала)
ряда динамики

.





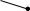





 Конструируется
как средняя
хронологическая
Конструируется
как средняя
хронологическая
 ,
,
где
 - период времени, представленный данным
- период времени, представленный данным
уровнем.

Исчисляется в соответствии с требованиями к
применению и исчислению среднего значения
признака
Методика исчисления среднего уровня ряда динамики
Интервальный
ряд абсолютных суммарных величин

где
 - абсолютная суммарная величина за весь
период ряда динамика
- абсолютная суммарная величина за весь
период ряда динамика
Интервальный ряд средних величин (расчет ведется по данным параллельных рядов):
 ,
,
где
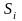 -
показатель числа единиц совокупности,
представленной средним уровнем признака
;
-
показатель числа единиц совокупности,
представленной средним уровнем признака
;
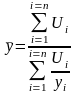 ,
,
где
показатель
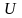 соответствует
величине (
соответствует
величине ( )
;
)
;
 .
.
Анализ интенсивности изменения во времени осуществляется с помощью показателей, получаемых в результате сравнения уровней. К таким показателям относятся:абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента. Показатели анализа динамики могут вычисляться на постоянной и переменной базах сравнения. При этом принято называть сравниваемый уровень отчетным, а уровень, с которым производится сравнение, базисным. Для расчета показателей анализа динамики на постоянной базе, каждый уровень ряда сравнивается с одним и тем же базисным уровнем. В качестве базисного выбирается либо начальный уровень в ряду динамики, либо уровень, с которого начинается какой-то новый этап развития явления. Исчисляемые, при этом, показатели называются базисными. Для расчета показателей анализа динамики на переменной базе, каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели анализа динамики называютсяцепными. Важнейшим статистическим показателем анализа динамики является абсолютный прирост (сокращение), т.е. абсолютное изменение, характеризующее увеличение или уменьшение уровня ряда за определенный промежуток времени. Абсолютный прирост с переменной базой называют скоростью роста.
Абсолютный прирост:
базисный

цепной

Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному, т.е. общему приросту за весь промежуток времени

Для оценки интенсивности, т.е. относительного изменения уровня динамического ряда за какой-либо период времени, исчисляют темпы роста (снижения). Интенсивность изменения уровня оценивается отношением отчетного уровня к базисному. Показатель интенсивности изменения уровня ряда, выраженный в долях единицы, называется коэффициентом роста, а в процентах – темпом роста. Эти показатели интенсивности отличаются только единицами измерения. Коэффициент роста (снижения)показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если этот коэффициент больше единицы) или какую часть (долю) уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы). Темп роста всегда представляет собой положительное число.
Коэффициент роста:
базисный:

цепной:

Темп роста:
базисный:

цепной:

Таким образом,

Между цепными и базисными коэффициентами роста существует взаимосвязь (если базисные коэффициенты исчислены по отношению к начальному уровню ряда динамики): произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста за весь период:

а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста.
Относительную оценку скорости измерения уровня ряда в единицу времени дают показатели темпа прироста (сокращения). Темп прироста (сокращения) показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения и вычисляется как отношение абсолютного прироста к абсолютному уровню, принятому за базу сравнения. Темп прироста может быть положительным, отрицательным или равным нулю, выражается он в процентах или в долях единицы (коэффициенты прироста).
Темп прироста:
базисный:

цепной:

Темп прироста (сокращения) можно получить, если из темпа роста, выраженного в процентах, вычесть 100%:

Коэффициент прироста получается вычитанием единицы из коэффициента роста:

При анализе динамики развития следует также знать, какие абсолютные значения скрываются за темпами роста и прироста. Чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Результат выражают показателем, который называют абсолютным значением (содержанием) одного процента прироста и рассчитывают как отношение абсолютного прироста к темпу прироста за этот период времени, %:

32 - блок видов денег;
Блок видов денег включает показатели ликвидных активов, используемых как деньги.
Наличные
деньги в обороте (наличная денежная
масса)

Наличные
деньги вне банковской системы
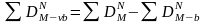
Наличные
деньги в кассах банков - сумма наличных
денег в кассах банков

Безналичная
денежная масса
– сумма безналичных денежных средств,
находящихся на депозитных счетах
коммерческих банков на момент
 и в среднем за период
и в среднем за период

Денежный мультипликатор – количество раз возрастания наличных денег поступивших в банковскую систему в результате безналичной эмиссии (банковской эмиссии)
Механизм банковской эмиссии

Но эта цепочка может продолжаться до тех пор, пока вся сумма наличных денег не будет превращаена в резервы банков
Таким
образом денежный мультипликатор будет
равен -

В
текущем наблюдении денежный мультипликатор
рассчитывается

А
чаще всего

Денежная
база (базовые деньги)
– количество наличных денег поступивших
в банковскую систему –

В
узком смысле представляет количество
наличных денег в обращении
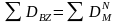
В
широком смысле включает дополнительно
корреспонденские счета и обязательные
резервы коммерческих банков в ЦБ
(наличные деньги в национальной валюте)

Ценные бумаги в денежном обороте – это номинальная стоимость государственных ценных бумаг (государственные краткосрочные облигации, государственные долгосрочные обязательства, государственные казначейские векселя и обязательства и прочие ценные бумаги), находящихся в обращении по состоянию на момент и среднем за период. Общая масса может изменяться в результате эмиссии ценных бумаг правительством. Но они могут продаваться и покупаться на открытом рынке в соответствии с действующим законодательством.
Мировые деньги – это деньги, признанные в качестве всеобщего универсального средства платежа в международных расчетах.
Включают – золото (в тройских унциях и долларах)
валюту – иностранные банкноты, чеки, монеты, признанные мировым сообществом
в качестве общих эквивалентов,
резервная позиция в МВФ
специальные права заимствования – эмитируемые МВФ платежные средства
предназначенные для регулирования сальдо платежных балансов, пополнения
официальных международных резервов, расчетов в МВФ
показатели рядов динамики
Анализ интенсивности изменения во времени осуществляется с помощью показателей, получаемых в результате сравнения уровней. К таким показателям относятся:абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента. Показатели анализа динамики могут вычисляться на постоянной и переменной базах сравнения. При этом принято называть сравниваемый уровень отчетным, а уровень, с которым производится сравнение, базисным. Для расчета показателей анализа динамики на постоянной базе, каждый уровень ряда сравнивается с одним и тем же базисным уровнем. В качестве базисного выбирается либо начальный уровень в ряду динамики, либо уровень, с которого начинается какой-то новый этап развития явления. Исчисляемые, при этом, показатели называются базисными. Для расчета показателей анализа динамики на переменной базе, каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели анализа динамики называютсяцепными. Важнейшим статистическим показателем анализа динамики является абсолютный прирост (сокращение), т.е. абсолютное изменение, характеризующее увеличение или уменьшение уровня ряда за определенный промежуток времени. Абсолютный прирост с переменной базой называют скоростью роста.
Абсолютный прирост:
базисный
цепной
Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному, т.е. общему приросту за весь промежуток времени
Для оценки интенсивности, т.е. относительного изменения уровня динамического ряда за какой-либо период времени, исчисляют темпы роста (снижения). Интенсивность изменения уровня оценивается отношением отчетного уровня к базисному. Показатель интенсивности изменения уровня ряда, выраженный в долях единицы, называется коэффициентом роста, а в процентах – темпом роста. Эти показатели интенсивности отличаются только единицами измерения. Коэффициент роста (снижения)показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если этот коэффициент больше единицы) или какую часть (долю) уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы). Темп роста всегда представляет собой положительное число.
Коэффициент роста:
базисный:

цепной:
Темп роста:
базисный:

цепной:
Таким образом,
Между цепными и базисными коэффициентами роста существует взаимосвязь (если базисные коэффициенты исчислены по отношению к начальному уровню ряда динамики): произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста за весь период:
а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста.
Относительную оценку скорости измерения уровня ряда в единицу времени дают показатели темпа прироста (сокращения). Темп прироста (сокращения) показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения и вычисляется как отношение абсолютного прироста к абсолютному уровню, принятому за базу сравнения. Темп прироста может быть положительным, отрицательным или равным нулю, выражается он в процентах или в долях единицы (коэффициенты прироста).
Темп прироста:
базисный:
цепной:
Темп прироста (сокращения) можно получить, если из темпа роста, выраженного в процентах, вычесть 100%:
Коэффициент прироста получается вычитанием единицы из коэффициента роста:
При анализе динамики развития следует также знать, какие абсолютные значения скрываются за темпами роста и прироста. Чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Результат выражают показателем, который называют абсолютным значением (содержанием) одного процента прироста и рассчитывают как отношение абсолютного прироста к темпу прироста за этот период времени, %:
31-
принцип построения средних величин. Виды средних величин
Средние величины вариационного ряда.
В основе формирования множества средних величин вариационного ряда лежит важнейшее понятие математической статистики - степенная средняя:
 ,
где
,
где

Наибольшее распространение получили следующие реализации степенной средней:
Средняя
арифметическая (при
 )
)
 ,
для которой имеем
,
для которой имеем

Средняя
гармоническая (при
 )
)
 ,
для которой имеем
,
для которой имеем
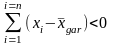
Средняя
квадратическая (при
 )
)
 ,
для которой имеем
,
для которой имеем

Средняя
кубическая (при
 )
)
 ,
для которой имеем
,
для которой имеем

Средняя
геометрическая (при
 )
)
 ,
для которой имеем
,
для которой имеем

Сумма
отклонений вариантов от степенной
средней
 принимает различные значения и по знаку
и по величине, согласно правила
можорантрости степенных средних :
принимает различные значения и по знаку
и по величине, согласно правила
можорантрости степенных средних :
 .
.
На этапе статистической обработки могут быть поставлены самые различные задачи исследования, для решения которых нужно выбрать соответствующую среднюю. При этом необходимо руководствоваться следующим правилом: величины, которые представляют собой числитель и знаменатель средней, должны быть логически связаны между собой.
Используются две категории средних величин:
степенные средние;
структурные средние.
Первая категория степенных средних включает: среднюю арифметическую, среднюю гармоническую, среднюю квадратическую и среднюю геометрическую.
Вторая категория (структурные средние) - это мода и медиана. Эти виды средних будут рассмотрены в теме «Ряды распределения».
Введем следующие условные обозначения:
 -
величины, для которых исчисляется
средняя;
-
величины, для которых исчисляется
средняя;
 -
средняя, где черта сверху свидетельствует
о том, что имеет место осреднение
индивидуальных значений;
-
средняя, где черта сверху свидетельствует
о том, что имеет место осреднение
индивидуальных значений;
 -
частота (повторяемость индивидуальных
значений признака).
-
частота (повторяемость индивидуальных
значений признака).
Различные средние выводятся из общей формулы степенной средней:
 (5.1)
(5.1)
при k = 1 - средняя арифметическая; k = -1 - средняя гармоническая; k = 0 - средняя геометрическая; k = -2 - средняя квадратическая.
Средние величины бывают простые и взвешенные. Взвешенными средними называют величины, которые учитывают, что некоторые варианты значений признака могут иметь различную численность, в связи с чем каждый вариант приходится умножать на эту численность. Иными словами, «весами» выступают числа единиц совокупности в разных группах, т.е. каждый вариант «взвешивают» по своей частоте. Частоту f называют статистическим весом или весом средней.
Средняя арифметическая - самый распространенный вид средней. Она используется, когда расчет осуществляется по несгруппированным статистическим данным, где нужно получить среднее слагаемое. Средняя арифметическая - это такое среднее значение признака, при получении которого сохраняется неизменным общий объем признака в совокупности.
Формула средней арифметической (простой) имеет вид
 (5.2)
(5.2)
где n - численность совокупности.
Например, средняя заработная плата работников предприятия вычисляется как средняя арифметическая:

Определяющими показателями здесь являются заработная плата каждого работника и число работников предприятия. При вычислении средней общая сумма заработной платы осталась прежней, но распределенной как бы между всеми работниками поровну. К примеру, необходимо вычислить среднюю заработную плату работников небольшой фирмы, где заняты 8 человек:

При расчете средних величин отдельные значения признака, который осредняется, могут повторяться, поэтому расчет средней величины производится по сгруппированным данным. В этом случае речь идет об использовании средней арифметической взвешенной, которая имеет вид
 (5.3)
(5.3)
показатели денежного обращения (макроэкономический уровень)
Макроэкономический блок включает показатели, позволяющие оценить взаимосвязь денег и денежного обращения с реальным сектором экономики и реальный уровень денежной массы
Номинальная
денежная масса
– количество денег на момент и в среднем
за период, находящихся в обращении
(запас активов в ликвидной форме)

Определяется как сумма наличной денежной массы и безналичной денежной массой.
Наличная денежная масса определяется
на момент балансовым методом по данным о эмиссии денег:

в среднем за период как средняя хронологическая моментного ряда динамики
Безналичная денежная масса определяется
на момент по данным бухгалтерского учета движения денег на банковских
счетах

в среднем за период как средняя хронологическая моментного ряда динамики
Денежный оборот - совокупность денежных операций, когда деньги используются в качестве средства обращения и средства платежа за период – поток денежной массы

Скорость
обращения денег
– число раз, которое каждый рубль
используется в качестве средства
обращения и средства платежа за период

Не
исключено

Реальная денежная масса – количество денег, необходимое для обеспечения реального объема производства (см. определение производства в системе национальных счетов)
Понять
смысл этого показателя можно исходя из
уравнения обмена записанного в следующей
форме

Откуда
следует что номинальная денежная масса
зависит от факторов производства, обмена
продукта и скорости оборота денег

Поскольку возможности исчисления обобщающих показателей натурального учета очень ограничены, то используют индексы. Тогда для номинальной денежной массы можно записать

Поскольку речь идет об обслуживании реального производства товаров и услуг, то имеем, что динамика реальной денежной массы будет определяться динамикой физического объема производства.
Уровень
монетаризации экономики
- удельный объем наличной денежной
массы на единичный объем ВВП

Покупательная способность денег - характеризует количество товаров, которое можно купить на 1 руб. денежной массы.
18 билет 1) Платежный баланс
Платежный баланс - это система показателей запасов и движения денежных средств. Поэтому имеет структуру:
Запас денежных средств на начало периода + Приток денежных средств за период =
= Отток денежных средств за период + Запас денежных средств на конец периода.
При этом система показателей платежного баланса должна отражать реальные процессы в сфере денежного обращения с такой глубиной и полнотой, которые обеспечивают необходимый для высокоэффективного управления объем информационных, объяснительных, эвристических и прогностических функций.
К системе показателей платежного баланса предъявляются следующие требования: отразить в организационном, экономическом, отраслевом и территориальном отношениях размещение денежных ресурсов, разнообразие источников поступления (притока) и направлений расходования (оттока) денежных средств.
Разнообразие в экономическом отношении основано на отражении многообразия экономических операций, которые связаны с приобретением ресурсов производства, реализацией результатов производства, образованием, распределением и использованием доходов и накоплений (в том числе и заимствованных на стороне), и которые обслуживаются системой денежных отношений (финансовой системой). Поэтому платежный баланс железнодорожного предприятия включает показатели, представляющие:
движение денежных средств по текущей деятельности, обеспечивающее выполнение основных производственно-хозяйственных функций:
в части поступления денежных средств:
поступления от реализации услуг по перевозкам,
поступления за ремонт подвижного состава на сторону,
поступления от прочих видов деятельности,
поступления прочих доходов,
поступления целевого финансирования на текущие цели,
в части направления денежных средств:
выплаты по заработной плате,
уплату налоговых платежей в бюджеты всех уровней и во внебюджетные фонды,
оплату всех видов ремонта, выполняемых сторонними организациями,
выплаты поставщикам и подрядчикам,
выплаты сторонним исполнителям отдельных видов работ и услуг, обеспечивающих текущую деятельность,
прочие расходы,
возврат выручки по услугам, перевыставляемым ОАО «РЖД» и другим соисполнителям,
расходы на погашение просроченной кредиторской задолженности;
движение денежных средств по инвестиционной деятельности, обслуживающее деятельность по расширенному воспроизводству основных средств и нематериальных активов, и финансовым вложениям:
в части поступления денежных средств:
выручку от реализации внеоборотных активов,
поступления от реализации финансовых вложений и иных оборотных активов,
проценты к получению,
поступления целевого финансирования на инвестиционные цели,
прочие поступления,
в части направления денежных средств:
расходы на приобретение основных средств,
расходы на модернизацию подвижного состава,
расходы на производство основных средств для собственных нужд,
- расходы на финансовые вложения (вклады в уставные (складочные) капиталы других организаций, государственные и муниципальные ценные бумаги, ценные бумаги других организаций, в том числе долговые ценные бумаги (облигации, векселя), предоставленные займы, депозитные вклады, в том числе проценты по депозитным вкладам),
прочие расходы по инвестиционной деятельности (в том числе на капитальное строительство объектов основных средств);
движение денежных средств по финансовой деятельности, связанное с осуществлением внешнего финансирования, призванного увеличивать денежные средства для финансового обеспечения основной и инвестиционной деятельности;
в части поступления денежных средств:
получение долгосрочных и краткосрочных кредитов и займов,
прочие поступления по финансовой деятельности, в том числе от эмиссии акций и целевое финансирование на финансовую деятельность,
в части направления денежных средств:
погашение кредитов и займов,
выплату дивидендов,
прочие расходы, в том числе погашение векселей.
В отраслевом отношении многообразие формируется за счет выделения конкретных видов деятельности, представляющих отрасли, для которых характер процессов притока и оттока денежных средств имеет столь существенные особенности, что с неизбежностью ставит проблемы их обязательного учета в процессе управления ими.
В условиях сложной корпоративной системы, какой является, например, ОАО «Российские железные дороги» организационный аспект отражает наличие системы взаимодействующих хозяйствующих субъектов различного уровня общности. Поэтому формируется единая система платежных балансов с элементами:
Платежный баланс ОАО, включающий сводный платежный баланс филиалов (железных дорог) и других структурных единиц (функциональных и отраслевых филиалов), в обобщенном виде отражающий функционирование присущих им денежных систем, центральный платежный баланс, отражающий процессы денежного обращения системы головной организации, консолидированный платежный баланс, обобщающий на принципах консолидации платежный сводный и центральный балансы,
Платежный баланс филиала соответствующего уровня, включающий сводный платежный баланс филиалов низового уровня и других структурных единиц, центральный платежный баланс, консолидированный платежный баланс.
Платежный баланс структурного подразделения.
Особенностью такой системы платежных балансов состоит в том, что в ней представлены не только отношения общности (часть - целое), но и, это очень важно, взаимодействия между денежными системами хозяйствующих объектов и по вертикали и по горизонтали.
Принцип консолидации в случае платежных балансов означает не просто обобщение одноименных показателей в их множестве, которые являются содержанием отчетных платежных балансах структурных единиц, включая сам аппарат данного уровня управления, а формирование новой системы показателей как содержание консолидированного сводного платежного баланса.
Такая система показателей исключает всякую возможность представления любых доходов и расходов, возникающих в результате взаимных расчетов между вышестоящим и нижестоящими структурными подразделениями, а также взаимных расчетов нижестоящих структурных подразделений между собой. В силу этого не показываются перечисление доходов с расчетных счетов структурных подразделений данного подчинения на расчетный счет данной организации; перечисление с расчетных счетов данной организации на расчетные счета нижестоящих структурных подразделений в порядке финансирования текущих расходов, а также перечисления возможных транзитных платежей. В результате такой консолидации, функционирование финансовой системы структурной единицы любого уровня представляется показателями общих запасов денежных средств и потоков только тех денежных и неденежных средств, которые поступают в систему из соответствующих источников и выбывают из системы по конкретным направлениям использования.
В условиях сложившейся системы производственных отношений между элементами ОАО «РЖД» различного уровня, платежный баланс объективно отражает операции, которые не связаны с движением денежных средств. К ним отнесятся операции
централизованной оплаты работ и услуг головным подразделением в рамках внутрихозяйственного финансирования текущей деятельности,
централизованного финансирования целевых программ ОАО «РЖД» (в размерах, относимых на долю филиала);
централизованные закупки товарно-материальных ценностей Росжелдорснабом в размере поступления этих средств в филиал;
оплаты работ, услуг, закупок товарно-материальных ценностей другими филиалами за филиал-бюджетодержатель.
Без отражения этой группы отношений невозможно полное описание экономической деятельности как системы потоков и запасов в их разнообразии, отображаемой в системах экономического учета, включая бухгалтерский учет.
В силу этого показатели платежного баланса отражают финансовые потоки, представленные потоками денежных средств, формируя платежный баланс денежных средств, и потоками централизованных и экстерриториальных платежей и поставок, формируя баланс неденежных операций.
Качественные особенности процессов, представленных системой показателей – абсолютных величин, отражают показатели – относительные величины: относительные величины структуры и относительные величины координации. Последние важны в первую очередь как характеристики пропорциональности между денежными потоками и запасами в их разнообразии.
2) Относительные величины структуры, координации, интенсивности, сравнения
Относительная величина структуры – характеризует долю отдельных частей в общей совокупности. Относительные величины структуры называют удельным весом единиц в общей совокупности.
 ,
где i
– число частей целого.
,
где i
– число частей целого.Относительные величины координации, характеризующие отношения отдельных частей совокупности с одной из них, принятой за базу сравнения (численность сел. жителей на 100 человек городских жителей).
 ,
где i,j
– число частей одного целого.
,
где i,j
– число частей одного целого.Относительные величины интенсивности – показатели, характеризующие меру распространения или развития данного явления в определенной среде, они рассчитываются как отношение абсолютной величины к размеру среды, в которой они находятся.
 ,
где А – степень распространение явления;
ВА - среда распространения явления
А.
,
где А – степень распространение явления;
ВА - среда распространения явления
А.
Относительные величины сравнения, получаются путем сравнения одноименных уровней, относящихся к разным объектам, территориям за один и тот же период или на один и тот же момент времени.
 ,
где МА - показатель первого одноименного
исследуемого объекта; МБ - показатель
второго одноименного исследуемого
объекта (база сравнения).
,
где МА - показатель первого одноименного
исследуемого объекта; МБ - показатель
второго одноименного исследуемого
объекта (база сравнения).
21 билет 1) Объект банковской статистики. Структура системы показателей
Объект изучения банковской статистики – деятельность банков и в первую очередь в части кредитно-расчетного обслуживания.
Призвана характеризовать банковскую систему как таковую. Традиционно ее принято представлять, распределяя показатели по следующим уровням:
исходный
базовые индексы
индексы сравнительной привлекательности условий банковской деятельности
удельные показатели развития банковской системы.
Исходные
Основные
1. Абсолютная величина банковских активов (по банкам на данной территории) –
-
 ;
;
2.
Уровень (индекс) инфляции –
 приравнивается к индексу потребительских
цен (согласно мировой практике) -
приравнивается к индексу потребительских
цен (согласно мировой практике) -
 ,
где
,
где
 ;
;
3.
Величина реальных активов (темп роста)
- -

по данным темпа роста номинальных активов:
4.
Доходы населения за предшествующий
период -

по данным о среднедушевых доходах и численности населения. – Предлагается рассматривать в качестве характеристики размера финансовых потоков банковской системы региона.
5.
Количество банков, зарегистрированных
на данной территории -
 ,
где
,
где

6.
Количество филиалов банков,
зарегистрированных на данной территории
-
 ,
,
где ;
7.
Количество банковских учреждений на
данной территории -
 ,
,
где
,
 ;
;
8.
Индекс количества банковских учреждений
в регионе -

где
среднерегиональное количество учреждений
рассчитывается согласно
 ;
;
9.
Среднее число филиалов, созданных банком
-
 ;
;
10.
Количество филиалов банков в регионе
-
 ;
;
11.
Объем кредитных вложений банков,
зарегестрированных в регионе -
 ;
;
12.
Доля кредитов в активах банка (банков)
- -
 .
.
2)Ряды распределения и их виды. Средние величины вариационного ряда: средняя арифметическая, мода, медиана.
Ряды распределения
Значения варьирующего признака |
|
|
… |
|
… |
|
Число единиц совокупности |
|
|
… |
|
… |
|
Правило
упорядочения:
 ,
если варьирующий признак – числительное
,
если варьирующий признак – числительное
 ,
если варьирующий признак атрибутивный.
,
если варьирующий признак атрибутивный.
Классификация рядов распределения
Р яды
распределения
яды
распределения
Атрибутивные Вариационные
Дискретные Интервальные
с равными с неравными
интервалами интервалами
Распределение рабочих по тарифному разряду
Тарифный разряд (варианты) |
1 |
2 |
3 |
4 |
5 |
6 |
Итого |
||||||||
Численность рабочих |
Чел. (частоты) |
10 |
20 |
130 |
190 |
150 |
60 |
560 |
|||||||
% к итогу (частости) |
1,79 |
3,57 |
23,21 |
33,93 |
26,79 |
10,71 |
100,00 |
||||||||
Распределение рабочих по размеру заработной платы
Уровень заработной платы, тыс.руб (варианты в форме интервалов) |
До 5,0 |
5,0 -10,0 |
10,0 -15,0 |
15,0 -20,,5 |
20,0 -25,0 |
Более 25,0 |
Итого |
||||||||
Численность рабочих |
Чел. (частоты) |
15 |
60 |
160 |
210 |
75 |
40 |
560 |
|||||||
% к итогу (частости) |
2,68 |
10,71 |
28,58 |
37,50 |
13,39 |
7,14 |
100,00 |
||||||||
Средние величины вариационного ряда.
В основе формирования множества средних величин вариационного ряда лежит важнейшее понятие математической статистики - степенная средняя:
, где
Наибольшее распространение получили следующие реализации степенной средней:
Средняя арифметическая (при ) , для которой имеем
Средняя гармоническая (при ) , для которой имеем
Средняя квадратическая (при ) , для которой имеем
Средняя кубическая (при ) , для которой имеем
Средняя геометрическая (при ) , для которой имеем
Сумма отклонений вариантов от степенной средней принимает различные значения и по знаку и по величине, согласно правила можорантрости степенных средних : .
Свойства средней арифметической.
,
что делает этот показатель наиболее предпочтительным из всех степенных средних
Если
 для всех
,
то
для всех
,
то

Если
 для всех
,
то
для всех
,
то

Если
 для всех
,
то
для всех
,
то
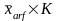
Если
 для всех
,
то
для всех
,
то