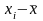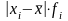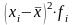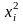- •При прочих равных условиях значение абсолютной величины определяется размером совокупности Виды абсолютных величин
- •Счет производства
- •Способы расчета дисперсии.
- •Расчет способом моментов
- •Классификация рядов динамики
- •Уровни ряда динамики Динамика явления по показателю
- •Методика исчисления среднего уровня ряда динамики
- •Способ моментов в расчете средней величины признака
- •Средние по положению Мода ( ) – вариант ( значение признака ) наибольшей численности (частоты).
- •3. Определение значения медианы:
- •Размах вариации - мерой различия вариантов служить не может. В случае ; ; , вариацию признака представляют:
- •Способы расчета дисперсии.
- •Расчет способом моментов
- •К расчету показателей вариации тарифного разряда
- •К расчету показателей вариации заработной платы работников
- •Виды дисперсии.
- •Сводка статистических данных
- •Виды сводки
- •Сводка состоит из следующих этапов:
- •Понятие и виды группировки
- •Группировка статистических данных
- •Виды группировок
- •Индекс цен
- •Индекс физического объема продукции.
- •Общий индекс исчисляется на основе категории стоимости продукции, когда . Агрегатный ; средний ;
- •Объект статистики страхования.
- •Уровни ряда динамики Динамика явления по показателю
- •Методика исчисления среднего уровня ряда динамики
- •Методика исчисления среднего уровня ряда динамики
- •Методика расчета среднего уровня ряда динамики (продолжение) Моментный ряд абсолютных суммарных величин
- •График состояния явления по показателю
- •Показатели изменения уровня ряда
- •Показатели изменения уровня ряда
- •К определению среднего темпа роста
- •1) Формула агрегатного индекса Пааше:
- •По методу начисления процентов различают:
- •При сроке пользования ссудой менее одного года:
- •2. Общий индекс валовой продукции:
- •3. Общий индекс численности поголовья:
Размах вариации - мерой различия вариантов служить не может. В случае ; ; , вариацию признака представляют:
; ; .
Потому мерой вариации может служить показатель – средняя из
Показатели вариации рассчитываются как средняя величина отклонений вариантов от средней.
Среднее линейное отклонение [ размерность признака]
для вариационного ряда - , где , для исходной совокупности - .
Дисперсия [безразмерная величина]
для вариационного ряда - ; для исходной совокупности - .
.
Способы расчета дисперсии.
Преобразуем .
Имеем:
где - средний квадрат вариантов.
.
Расчет способом моментов
Преобразование исходных значений признака : ;
Расчет средних величин - момента первого порядка: ; ,
- момента второго порядка: ; ;
3, расчет дисперсии по формуле .
Среднее квадратическое отклонение - [ размерность признака]
для вариационного ряда - ; для исходной совокупности - .
Соотношение показателей вариации: и
В случае двух признаков ( ) и ( ) не сопоставимы.
Поэтому конструируется относительный показатель – коэффициент вариации
признака , ; признака ,
Коэффициенты вариации различных распределений сопоставимы. В частности их можно сопоставить с коэффициентом вариации нормального распределения независимой случайной величины -
К расчету показателей вариации тарифного разряда
Тарифный разряд, |
Численность рабочих , |
|
|
|
|
|
|
1 |
10 |
-3,125 |
3,125 |
31,25 |
97,65625 |
1 |
10 |
2 |
20 |
-2,125 |
2,125 |
42,5 |
90,3125 |
4 |
80 |
3 |
130 |
-1,125 |
1,125 |
146,25 |
164,5313 |
9 |
1170 |
4 |
190 |
-0,125 |
0,125 |
23,75 |
2,96875 |
16 |
3040 |
5 |
150 |
0,875 |
0,875 |
131,25 |
114,8438 |
25 |
3750 |
6 |
60 |
1,875 |
1,875 |
112,5 |
210,9375 |
36 |
2160 |
итого |
560 |
х |
х |
487,5 |
681,25 |
х |
10210 |
Расчет
среднего линейного отклонения:
 ,
разряд.
,
разряд.
Расчет
дисперсии: 1)
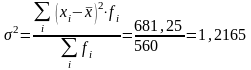
2)
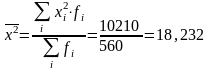
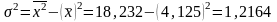
Расчет
среднеквадратического отклонения:
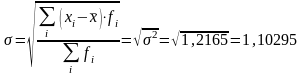 ,
разряд
,
разряд
Проверка:

Расчет
коэффициента корреляции:
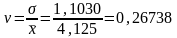 .
.