К определению среднего темпа роста

Место темпов роста в системе показателей ряда динамики:

.

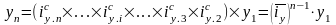Поэтому средний темп роста – есть средняя геометрическая из цепных темпов:

Учитывая, что и , имеем расчетную формулу:

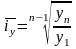
Темп прироста – показатель изменения уровня ряда в виде относительного величины абсолютного прироста:

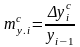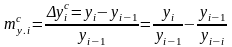цепной , причем и ;

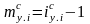базисны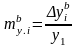й и

Как обобщение множества цепных темпов прироста базисный темп прироста может быть представлен только в такой форме:

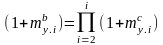
Как следствие, средний темп прироста - средняя из множества цепных может быть представлен в виде

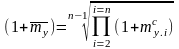
Поэтому рассчитывается как 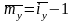, откуда .

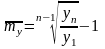Абсолютное значение 1% (цепного) прироста – показатель значимости относительной меры изменения уровня ряда.

Надо иметь в виду, что 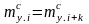[%] не означает , что ,

поскольку и , а .

Рассчитывается как ,

что следует из .

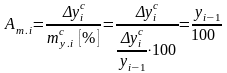Показатели динамики среднего расстояния перевозки пассажиров

Год	Среднее расстояние перевозки, км	Абсолютный прирост, км		Темп роста,%		Темп прироста, %		Абсолютн. значение 1% прироста, км
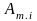
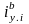
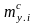
		цепной	базисный	цепной	базисный	цепной	базисный
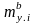
1	700
2	669	-31	-31	95,57	95,57	-4,43	-4,43	7,00
3	690	21	-10	103,14	98,57	3,14	-1,43	6,69
4	710	20	10	102,90	101,43	2,90	1,43	6,90
5	713	3	13	100,42	101,86	0,42	1,86	7,10
Итого	Х	13	Х	Х	Х	Х	Х	Х

где, например:

; … ; ;

;

;

; … ; ; ;

;

; ; …

…; ; ; ; ;

; … ;

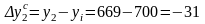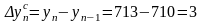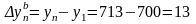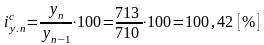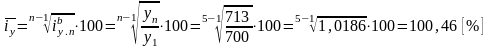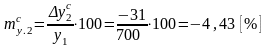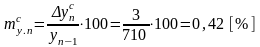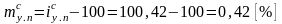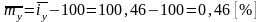
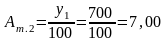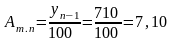
№2.

1.Основные методологии статистики финансов.

Основы методологии статистики финансов.

Почему финансы становятся объектом статистики и более того без статистики управлять финансами невозможно?

Вся совокупность финансовых отношений, складывающихся в связи с осуществлением массовых экономических операций в их большом разнообразии – есть множество взаимосвязанных и взаимообусловленных явлений, каждое из которых представляет собой статистическую совокупность.

Познать такие явления можно, только опираясь на меру, обеспечивающую возможность обобщения всего множества фактов проявления конкретных явлений, и отразить поведение этих явлений на уровне законов и их проявления в конкретных условиях места и времени. Как следствие, познание финансов в процессе управления ими основано на категории статистического показателя.

Категория статистического показателя требует строгого определения конкретных явлений в их схожести и различиях. Поэтому в статистике явления в сфере финансов получают строгую определенность, а затем и строгое измерение.

Финансовые отношения, как и финансы в целом складываются под влиянием большого числа факторов, представляющих как деятельность собственно финансовой системы, так и происходящее вовне, в том числе факторы места и времени. Отразить механизмы влияния факторов можно, только опираясь на количество в единстве с качеством явлений, так как количество динамично при сохранении качественной определенности.

Описать механизм взаимосвязи между явлениями и определяющими их поведение факторами можно, только опираясь на систему показателей.

Поэтому в статистике финансов используются все элементы статистической методологии, связанной с познанием, в широком смысле, количественной стороны явлений и процессов в сфере финансов. Это

· массовое статистическое наблюдение,

· группировки единичных фактов проявления конкретных явлений, и исчисление статистических показателей объемных в виде абсолютных величин, и качественных, в виде средних и относительных величин, включая показатели вариации, корреляции и регрессии,

· построение динамических и статических рядов и исчисление показателей динамики и сравнения, в том числе и динамических и статических индексов,

· расчеты показателей влияния факторов на динамику и различия явлений в статике с использованием аппарата моделирования на основе информационных моделей явлений,

· исчисление показателей основной тенденции и неравномерности развития во времени и т.п.

2.Уравнение регрессии и его структура.Метод наименьшего квадрата-параметры уравнения регрессии.

Эмпирическая линия регрессии, построенная по точкам:

 

 

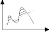
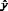 – сглаженная линия (уравнение прямой) – теоретические значения.

Регрессионный анализ заключается в нахождении формулы для выражения функции 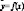 , причем эта функция должна быть приведена таким образом, чтобы расхождения между фактическими данными и полученными по формуле были минимальными.

, где   – случайности отклонения, т.е.

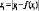
 – сглаживающая линия, 

Изломы этой линии (штрих) указывает на действия случайных факторов, которые не учитываются в модели.

Для того чтобы абстрагироваться от влияния случайных факторов используют выравнивание ломаной линии по некоторой плавной сглаживающей кривой.

Эту сглаживающую линию называют теоретической линией регрессии (линия регрессии).

Она отражает теоретическую формулу связи. Эта связь возникает при условии полного взаимопоглощения всех прочих факторов случайных по отношению к фактору x.

Уравнение, которое описывает теоретическую линию регрессии называют уравнением регрессии.

 

где f(x) – какая-то неизвестная функция, а   – средняя величина признака, которая изменяется.

f(x) – функция, которая устанавливает вид однозначной зависимости между этими величинами – это расчетные теоретические значения.

Наиболее часто используются следующие типовые функции: линейная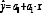   

параболическая связь  и другие.

Наиболее часто применяется линейная зависимость:  , где а0 – свободный член, а1 – коэффициент регрессии, который указывает на сколько единиц в среднем меняется результативный признак при изменении факторного значения на единицу его измерения.

В математической статистике доказано, что

 т.е. дает совпадение в сумме: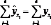 

Используя критерий минимизации можно получить значения неизвестных, коэффициент уравнения регрессии:

Система нормальных уравнений:

 

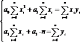
и, соответственно расчет коэффициента регрессии a1 и свободного члена a0:

 

При использовании других типовых функций образуются иные системы нормальных уравнений, для которых определены значения искомых параметров.

Решив уравнение регрессии и получив коэффициент уравнения, их необходимо проверить на неслучайность, т.е. статистическую значимость.

Метод наименьших квадратов один из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным. Метод основан на минимизации суммы квадратов остатков регрессии.

Необходимо отметить, что собственно методом наименьших квадратов можно назвать метод решения задачи в любой области, если решение заключается или удовлетворяет некоторому критерию минимизации суммы квадратов некоторых функций от искомых переменных. Поэтому метод наименьших квадратов может применяться также для приближённого представления (аппроксимации) заданной функции другими (более простыми) функциями, при нахождении совокупности величин, удовлетворяющих уравнениям или ограничениям, количество которых превышает количество этих величин и т. д.

Пусть задана некоторая (параметрическая) модель вероятностной (регрессионной) зависимости между (объясняемой) переменной y и множеством факторов (объясняющих переменных) x

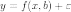
где   — вектор неизвестных параметров модели

 — случайная ошибка модели.

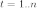Пусть также имеются выборочные наблюдения значений указанных переменных. Пусть   — номер наблюдения ( ). Тогда   — значения переменных в  -м наблюдении. Тогда при заданных значениях параметров b можно рассчитать теоретические (модельные) значения объясняемой переменной y:

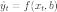
Тогда можно рассчитать остатки регрессионной модели — разницу между наблюдаемыми значениями объясняемой переменной и теоретическими (модельными, оцененными):

Величина остатков зависит от значений параметров b.

Сущность МНК (обычного, классического) заключается в том, чтобы найти такие параметры b, при которых сумма квадратов остатков 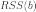  (англ. Residual Sum of Squares^[1]) будет минимальной:

где:

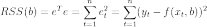
В общем случае решение этой задачи может осуществляться численными методами оптимизации (минимизации). В этом случае говорят о нелинейном МНК (NLS или NLLS — англ. Non-Linear Least Squares). Во многих случаях можно получить аналитическое решение. Для решения задачи минимизации необходимо найти стационарные точки функции  , продифференцировав её по неизвестным параметрам b, приравняв производные к нулю и решив полученную систему уравнений:

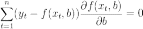
Если случайные ошибки модели имеют нормальное распределение, имеют одинаковую дисперсию и некоррелированы между собой, МНК-оценки параметров совпадают с оценками метода максимального правдоподобия (ММП).

Билет9.

1.счета накопления.

Все  счета  условно делятся на две группы:  счета  текущих операций и  счета   накопления . К первой группе текущих операций относятся  счета  производства, распределения первичных и вторичных доходов, распределения доходов в натуральной форме, использования располагаемого дохода, использования скорректированного дохода. К группе  счетов   накопления  относятся  счет  операций с капиталом, финансовый  счет ,  счет  переоценки и  счет  других изменений в активах.

Финансовый счет – это счет макроэкономического характера, составляющийся параллельно с другими счетами СНС.

Финансовый счет включается в группу счетов накопления. Правая сторона счета – это операции по принятию финансовых обязательств. Левая сторона – операции по приобретению финансовых активов.

Регистрация операций в финансовом счете осуществляется по изменениям за период финансовых активов и операций, а не по их абсолютной величине.

Информация, получаемая на основе СНС, нужна органам государственного управления, предприятиям и международным организациям.

Создается для развития и повышения эффективности внешнеторговой деятельности система внешнеторговой информации, управление которой производится федеральным органом исполнительной власти.

2.индексы.понятие и виды.

В статистике индек-

сом называют показатель относительного изменения данного уровня исследуемого явле-

ния по сравнению с другим его уровнем, принятым за базу сравнения. В качестве такой

базы может быть использован или уровень за какой-либо прошлый период времени (ди-

намический индекс), или уровень того же явления по другой территории (территориаль-

ный индекс). Индексы являются незаменимым инструментом исследования в тех случаях,

когда необходимо сравнить во времени или пространстве две совокупности, элементы

которых непосредственно суммировать нельзя.

В целом, индексный метод направлен на решение следующих задач:

1) характеристика общего изменения уровня сложного социально-экономического

явления;

2) анализ влияния каждого из факторов на изменение индексируемой величины пу-

тем элиминирования воздействия прочих факторов;

3) анализ влияния структурных сдвигов на изменение индексируемой величины.

В дальнейшем изложении индексного метода будут использоваться следующие

общепринятые обозначения:

i – индивидуальный индекс;

I – сводный индекс;

p – цена;

q – количество;

1 – текущий период;

0 – базисный период.

Простейшим показателем, используемым в индексном анализе, является индиви-

дуальный индекс, который характеризует изменение во времени экономических величин,

относящихся к одному объекту:

p i =

0

1

p

p – индекс цены,

где 1 p – цена товара в текущем периоде;

0 p – цена товара в базисном периоде;

Изменение физической массы проданного товара в натуральном

Все экономические индексы можно классифицировать по сле­дующим признакам:

• степень охвата явления;

• база сравнения;

• вид весов (соизмерителя);

• форма построения;

• характер объекта исследования;

• объект исследования;

• состав явления;

• период исчисления.

По степени охвата явления индексы бывают индивидуаль­ные и сводные. Индивидуальные индексы служат для харак­теристики изменения отдельных элементов сложного явления. Их примером могут быть изменения объема производства от­дельных видов продукции (телевизоров, электроэнергии и т. д.), а также цен на акции какого-либо предприятия. Для измерения динамики сложного явления, составные части которого непос­редственно несоизмеримы (изменения физического объема продукции, включающей разноименные товары, индекса цен, акций предприятий региона и т. п.), рассчитывают сводные, или общие, индексы.

Если индексы охватывают не все элементы сложного явления, а только часть их, то такие индексы называются групповыми или субиндексами, например индексы физического объема продукции по отдельным отраслям промышленности, индексы цен по груп­пам продовольственных и непродовольственных товаров. Группо­вые индексы отражают закономерности в развитии отдельных ча­стейизучаемых явлений. В таких индексах проявляется их связь с методом группировок.

По базе сравнения все индексы можно разделить на две груп­пы: динамические и территориальные. Первая группа индексов отражает изменение явления во времени. Например, индекс цен на продукцию в 1996 г. по сравнению с предыдущим годом; индекс стоимости потребительской корзины в августе по сравнению с июлем 1997 г.

При исчислении динамических индексов происходит сравнение значения показателя в отчетный период со значением этого же показателя за предыдущий период, который называют базисным. Однако в качестве последнего могут быть использованы и прогноз­ные, и плановые показатели. Динамические индексы бывают базисные и цепные.

Вторая группа (территориальные) применяется для межрегиональных сравнений. Большое значение эти индексы име­ют в международной статистике при сопоставлении показателей социально-экономического развития различных стран. Например, индекс цен на фототовары в Италии по сравнению с Германией, индекс стоимости потребительской корзины в Москве по сравне­нию с Санкт-Петербургом.

По виду весов индексы бывают с постоянными и переменны­ми весами.

В зависимости от формы построения различаются индексы агрегатные и средние. Последние делятся на арифметические и гармонические. Агрегатная форма общих индексов является основ­ной формой экономических индексов. Средние индексы - производные, они получаются в результате преобразования агрегатных индексов.

По характеру объема исследования общие индексы подраз­деляются на индексы количественных (объемных) и качественных показателей. В основе такого деления индексов лежит вид индек­сируемой величины. К первой группе индексов относятся, напри­мер, индексы объема продаж долларов США на Московской меж­банковской валютной бирже, а ко второй - индекс курса немецкой марки.

По объекту исследования индексы бывают: производительно­сти труда, себестоимости, физического объема продукции, стоимо­сти продукции и т. д.

По составу явления можно выделить две группы индексов: постоянного (фиксированного) состава ипеременного состава. Деление индексов на эти две группы используется для анализа динамики средних показателей.

По периоду исчисления индексы подразделяются на годовые, квартальные, месячные, недельные.

 

4. Виды оценок показателей системы национальных счетов

В практике составления СНС и межотраслевого баланса (МОБ) применяются следующие виды цен:

• рыночные цены — цена производителя и цена покупателя;

• основные цены;

• факторные цены.

Процесс формирования цен, используемых в СНС и в МОБ, их состав по элементам, их связь и отличия отражает рис. 6.2.

Факторная цена используется в межотраслевом балансе. Цены потребителя (конечного потребления) представляют собой рыночные цены. Показатели СНС оцениваются преимущественно в РЫНОЧНЫХ ценах.

Рис. 6.2. Формирование цены в СНС

Рыночные цены — это цены производителей, основные цены и цены покупателей. Применение той или иной цены определяется по фактическому их использованию при осуществлении тех или иных операций.

Рыночная цена производителя — это цена, получаемая производителем за реализуемую единицу продукта или услуги, включающая налоги на продукты (кроме налога на добавленную стоимость и налогов на импорт) и исключающая субсидии на продукты (налоги, за исключением субсидий, представляют собой чистые налоги).

Рыночная цена покупателя — цена, уплаченная покупателем за продукты и услуги, включая все чистые налоги на продукты и торгово-транспортную наценку.

Основная рыночная цена — цена, получаемая производителем за единицу реализованного продукта или услуги, без налогов на продукты, но с включением субсидий на продукты. Она применяется для устранения влияния различных ставок налогов и субсидий в различных отраслях экономики.

Оценка осуществляется в СНС по ценам, фактически используемым в операциях (т. е. в текущих ценах).

Производство и использование валового внутреннего продукта оцениваются в текущих рыночных ценах, преобладающих в период, к которому относится его производство или использование.

Все показатели в текущих ценах, в том числе показатели изменения запасов материальных оборотных средств и потребления основного капитала, исчисляются в средних ценах рассматриваемого периода.

ВВП (как и ВНП) может оцениваться по факторной стоимости и в рыночных ценах покупателя. Оценка по факторной стоимости включает в себя только, издержки производства, т. е. потребление основного капитала, оплату труда и прибыль. В рыночной цене сверх того учитываются также чистые косвенные налоги.

Важным аспектом оценки продукции является отнесение расходов по доставке на счет производителя или потребителя. Так, цена производства равняется стоимости товара на предприятии производителя, т. е. не включает затраты на доставку товара потребителю. Цена потребления, наоборот, включает и торговые, и транспортные наценки, относящиеся к реализации данного товара. Понятия «цена производства» и «цена потребления» относятся к рыночным ценам.

Добавленная стоимость по основным ценам складывается из оплаты труда, прибыли и чистых косвенных налогов на производство.

Она отличается от добавленной стоимости по факторным ценам на сумму чистых косвенных налогов на производство. Если добавленную стоимость по основным ценам увеличить на сумму чистых косвенных налогов на продукты и на импорт, то образуется добавленная стоимость по рыночным ценам. Этот показатель в СНС 1993 является центральным показателем, характеризующим конечные результаты экономической деятельности хозяйствующих субъектов РФ.

В СНС ООН 1993 г. уточнены методы оценки отдельных элементов товаров и услуг, принимаемых во внимание в расчетах ВВП. В первую очередь это относится к оценке валового выпуска товаров и услуг. Так, наряду с традиционной оценкой этого показателя в ценах производителя рекомендуется оценивать валовой выпуск в основных ценах, которые включают субсидии на продукты, но не включают налоги на продукты.

Прежде всего основные цены больше подходят для оценки ресурсов, получаемых производителями товаров и услуг.

Надо, однако, подчеркнуть, что следствием оценки указанных потоков в основных ценах является то, что сумма валовой добавленной стоимости (ВДС) в основных ценах всех отраслей народного хозяйства не равна ВВП в ценах конечного использования (рыночных ценах).

Взаимосвязь между показателями, рассчитанными в различных ценах, можно представить следующим образом:

1. Промежуточное потребление + оплата труда + валовая прибыль = ВДС в факторных ценах.

2. ВДС в факторных ценах + косвенные налоги на производство - субсидии на производство = ВДС в основных ценах.

3. ВДС в основных ценах + косвенные налоги на продукты - субсидии на продукты = ВДС в ценах производителя.

4. ВДС в ценах производителя + торгово-транспортная наценка =  ВДС в рыночных ценах (ВВП в рыночных ценах).

Продукты, предназначенные к реализации и не принимающие форму товара, оцениваются по рыночным ценам на аналогичные товары, реализуемым на рынке, или по себестоимости, если рыночная цена отсутствует; нерыночные услуги оцениваются в размере фактических текущих затрат на их производство; промежуточное потребление в составе валового выпуска отраслей оценивается в ценах покупателя; разность между валовым выпуском по основным ценам и промежуточным потреблением позволяет получить добавленную стоимость по основным ценам.

Переоценка в сопоставимые цены проводится как по произведенному валовому внутреннему продукту, так и по показателям его использования.

С учетом специфических условий развития российской экономики, высокой инфляции и недостатка первичной информации переоценка показателей производства ВВП в сопоставимые цены осуществляется с использованием метода прямого дефлятирования (переоценка добавленной стоимости отраслей с использованием индекса цен выпуска каждой отрасли) или метода экстраполяции базисного уровня добавленной стоимости отрасли по каким-либо индексам физического объема или натуральным индикаторам, адекватно отражающим динамику развития производства в данной отрасли. В качестве таких индикаторов применяются либо показатели численности занятых в данной отрасли (например,  численность занятых в органах государственного управления и численность военнослужащих использовалась для экстраполяции показателей добавленной стоимости в отраслях «Управление» и «Оборона»), либо натуральные показатели, характеризующие основную деятельность этой отрасли (например, численность детей, обучающихся в школах, использовалась для переоценки добавленной стоимости в отрасли «Образование»).

Для переоценки в сопоставимые цены показателей использования ВВП применяются:

• индекс потребительских цен — для расходов на конечное потребление домашних хозяйств;

• натуральные индикаторы и численность занятых в отраслях — для расходов государственных учреждений и некоммерческих организаций, обслуживающих домашние хозяйства;

• индекс цен капитальных вложений — для накопления основного капитала;

• индексы цен в промышленности и сельском хозяйстве — для изменения запасов материальных оборотных средств;

• индексы цен на экспортную и импортную продукцию с учетом изменения обменного курса рубля — для экспорта и импорта.

Основные понятия статистики: статистическая совокупность и признак

1. Статистическая совокупность – это множество единиц изучаемого явления, объединенных единой качественной основой, общей связью, но отличающихся друг от друга отдельными признаками. Таковы, например, совокупность домохозяйств, совокупность семей, совокупность предприятий, фирм, объединений и т.п.

Совокупность называется однородной, если один или несколько изучаемых существенных признаков ее объектов являются общими для всех единиц.

Совокупность, в которую входят явления разного типа, считается разнородной. Совокупность может быть однородна в одном отношении и разнородна в другом. В каждом отдельном случае однородность совокупности устанавливается путем проведения качественного анализа, выяснения содержания изучаемого общественного явления.

2. Признак – это качественная особенность единицы совокупности.

По характеру выражения различают атрибутивные и

количественные признаки:

• атрибутивные (описательные) – выражаются словесно, например, пол, национальность, образование и др. По ним можно получить итоговые сведения о количестве статистических единиц, обладающих даннымзначением признака;

• количественные – выражаются числовой мерой (возраст, стаж работы, объем продаж, размер дохода и т.д.) По ним можно получить итоговые данные о количестве единиц, обладающих конкретным значением признака, и суммарное или среднее значение признака по совокупности.

По характеру вариации признаки делятся на:

• альтернативные - могут принимать только одно из двух возможных значений признака. Это признаки обладания или не обладания чем-либо. Например, пол, семейное положение, в маркетинговых или политологических исследованиях - ответ на вопрос в форме «да или нет»;

• дискретные – количественные признаки принимающие только отдельные значения, без промежуточных между ними - как правило целочисленные, например, разряд рабочего, число детей в семье и т.д.);

• непрерывные – количественные признаки, принимающие любые значения. На практике они, как правило, округляются в соответствии с принятой точностью (например: бухгалтерская прибыль по балансу в рублях, налоговая по налоговым регистрам – в тыс. руб.

По отношению ко времени различают:

• моментные признаки, характеризующие единицы совокупности на критический момент временинапример, стоимость основных производственных фондов (ОПФ) определяется на 01.01. и 31.12 соответствующего года как стоимость ОПФ на начало и конец отчётного года;

• интервальные признаки, характеризующие явление за определённый временной период ((год, квартал, месяц и т.д.), например, сменная выработка, дневная выручка, годовой объём продаж и т.д.

По характеру взаимосвязи признаки делятся на:

• факторные, вызывающие изменения других признаков, либо создающие возможности для изменений значений других признаков. Факторные признаки подразделяются соответственно на признаки причины и признаки условия;

• результативные (признаки следствия), зависящие от вариации других признаков. Например, стоимостной объём выпуска продукции является результативным признаком, величина которого зависит от факторных признаков - численности работников и производительности труда.

20.  Показатели использования оборотных средств

Оборотные средства — это средства, авансируемые организациями для поддержания непрерывности процесса производства и обращения и возвращающиеся в организации в составе выручки от реализации продукции в той же денежной форме, с которой они начали свое движение.

Для оценки эффективности использования оборотных средств применяются показатели оборачиваемости оборотных средств. Основными из них являются следующие:

• средняя продолжительность одного оборота в днях;

• количество (число) оборотов, совершаемых оборотными средствами в течение определенного периода времени (год, полугодие, квартал), иначе — коэффициент оборачиваемости;

• сумма занятых оборотных средств, приходящихся на 1 рубль реализованной продукции (коэффициент загрузки оборотных средств).

Если оборотные средства проходят все стадии кругооборота, например, за 50 дней, то первый показатель оборачиваемости (средняя продолжительность одного оборота в днях) составит 50 дней. Этот показатель приблизительно характеризует среднее время, которое проходит от момента приобретения материалов до момента реализации продукции, изготовленной из этих материалов. Данный показатель может быть определен по следующей формуле:

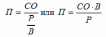
• П — средняя продолжительность одного оборота в днях;

• СО — средний остаток оборотных средств за отчетный период;

• Р — реализация продукции за этот период (за вычетом налога на добавленную стоимость и акцизов);

• В — число дней в отчетном периоде (в году — 360, в квартале — 90, в месяце — 30).

Итак, средняя продолжительность одного оборота в днях исчисляется как отношение среднего остатка оборотных средств к однодневному обороту по реализации продукции.

Показатель средней продолжительности одного оборота в днях может быть исчислен и другим способом, как отношение числа календарных дней в отчетном периоде к количеству оборотов, совершенных оборотными средствами за этот период, т.е. по формуле: П = В/ЧО, где ЧО — число оборотов, совершенных оборотными средствами за отчетный период.

Второй показатель оборачиваемости — число оборотов, совершаемых оборотными средствами за отчетный период (коэффициент оборачиваемости) — также может быть получен двумя способами:

• как отношение реализации продукции за вычетом налога на добавленную стоимость и акцизов к среднему остатку оборотных средств, т.е. по формуле: ЧО = Р/СО;

• как отношение числа дней в отчетном периоде к средней продолжительности одного оборота в днях, т.е. по формуле: ЧО = В/П .

Третий показатель оборачиваемости (сумма занятых оборотных средств, приходящихся на 1 рубль реализованной продукции или иначе — коэффициент загрузки оборотных средств) определяется одним способом как отношение среднего остатка оборотных средств к обороту по реализации продукции за данный период, т.е. по формуле: СО/Р.

Этот показатель выражается в копейках. Он дает представление о том, сколько копеек оборотных средств затрачивается для получения каждого рубля выручки от реализации продукции.

Наиболее распространенным является первый показатель оборачиваемости, т.е. средняя продолжительность одного оборота в днях.

Наиболее часто оборачиваемость исчисляется за год.

Принципы построения общих индексов

Индексом в статистике называют относительный показатель,

характеризующий изменение величины какого-либо явления (про­стого или сложного,

состоящего из соизмеримых или несоизмери­мых элементов) во времени,

пространстве или по сравнению с лю­бым эталоном (нормативом, планом, прогнозом

и тд.). Когда рассматривается сопоставление уровней изучаемого явления во

времени, то говорят об индексах динамики, в про­странстве — о

территориальных индексах, при сопоставлении с уровнем, например, договорных

обязательств — об индексах вы­полнения обязательств и т.д. Основным

элементом индексного отношения яв­ляется индексируемая величина.

Индексный метод имеет свою терминологию и символику. Каждая индексируемая

величина имеет обозначение: q - количество (объем) какого-либо продукта в

натуральном выражении (от латинского слова quantitas); р - цена единицы

товара (от латинского слова pretium); z - себестоимость единицы

продукции; t - затраты времени на производство единицы продукции

(трудоемкость); w - выработка продукции в стоимостном выражении на одного

работни­ка или в единицу времени;

v - выработка продукции в натуральном выражении на одного работни­ка или в

единицу времени; - Т - общие затраты времени (Г = tq) или численность

работников;

П -_ посевная площадь; У - урожайность отдельны* культур и т.д. .pq -

общая стоимость произведенной продукции данного вида или про­данных товаров

данного вида (товарооборот, выручка); zq - затраты на производство всей

продукции (издержки производства); УП - валовой сбор отдельной культуры.

Чтобы различать, к какому периоду относятся индексируе­мые величины, принято

возле символа индекса внизу справа ставить подстрочные знаки: 1 - для

сравниваемых (текущих, от­четных) периодов и 0 — для периодов, с которыми

производит­ся сравнение (базисных периодов). Если изменение явлений изучается

за ряд периодов, то каждый из периодов обозначается соответственно

подстрочными знаками 0, 1, 2, 3 и т.д.

Индивидуальные индексы обозначаются буквой / и снабжаются подстрочным

знаком индексируемого показателя: так i_q — ин­дивидуальный

индекс объема произведенной продукции отдель­ного вида или количества (объема)

проданного товара данного вида, i_p — индивидуальный индекс

цен и т.д.

Общий индекс обозначается буквой J_p и также

сопровождает­ся подстрочным знаком индексируемого показателя: Например, J

_p — общий индекс цен; J_z — общий индекс

себестоимости.

Индивидуальные индексы относятся к одному элементу (явлению) и не требуют

суммирования данных. Они представляют собой отно­сительные величины

динамики, выполнения обязательств, сравнения. Выбор базы сравнения

определяется целью исследования.

Расчет индивидуальных индексов прост, их определяют вы­числением отношения

двух индексируемых величин:

Индивидуальный индекс физического объема продукции iq рассчитывается по

формуле .

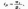где q1, q0 — количество (объем)

произведенного одноименного то­вара в текущем (отчетном) и базисном периодах

соот­ветственно.

Индивидуальный индекс цен:

где q1, p0 — цена единицы

одноименной продукции в отчетном и базисном периодах соответственно.

Индивидуальные индексы других показателей строятся аналогично. С аналитической

точки зрения индивидуальные индексы характе­ризуют изменения

индексируемой величины в текущем периоде по сравнению с базисным, т. е. во

сколько раз она возросла (умень­шилась) или сколько процентов составляет ее

рост (снижение). Значения индексов выражают в коэффициентах или процентах.

Каждый качественный показатель связан с тем или иных объемным показателем, в

расчете на единицу которого он исчисляется. Так, с объемом произведенной

(проданной)" продукции связаны такие качественные показатели, как цена р,

себестоимость z и трудоемкость t.

Рассмотрим принципы построения агрегатных индексов качественных

показателей на примере индекса цен.

Поскольку этот индекс характеризует изменение цен, индек­сируемой величиной

в нем будет цена товара. Влияние количества проданных товаров должно

быть устранено, а это возможно только в том случае, если количество продаваемых

товаров не­изменно в оба периода, т. е. количество товаров одного из пе­риодов

принято в качестве весов индекса.

При построении индекса цен в качестве весов индекса обыч­но берут

количество товаров, проданных в текущем (отчетном) периоде. Это

объясняется тем, что такое исчисление индекса цен позволяет определить не

только относительное изменение цен (путем деления числителя индекса

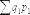
на его знамена­тель ,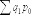

но и абсолютную экономию (-) или абсолютный перерасход (+) денежных средств

покупателей в результате из­менения цен на эти товары (как разность между

числителем и знаменателем индекса):

.

Агрегатный индекс с отчетными весами впервые предложен в 1874 г.

немецким экономистом Г. Паше и носит его имя: