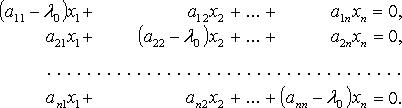AiG_voprosy_1

48. Матрица линейного оператора, ее преобразование при переходе к новому базису.

 Матрица линейного оператора 

     Матрица линейного оператора   в базисе ( ) - матрица

столбцами которой являются столбцы образов базисных векторов   оператора f, т.е.  

  Линейный оператор называется невырожденным, если 

49. Действия с линейными операторами.

Операторы A и B, действующие из X в Y называются равными, если A(x) = B(x) для всех x из X :

A: X → Y,  B: X → Y,  A = B  если  A(x) = B(x), ∀x∈X.

Операторы A и B действуют из X в Y . Оператор C, действующий из X в Y, называется суммой операторов A иB, если C(x) = A(x) + B(x) для всех x из X :

A: X → Y,  B: X → Y,  C = A + B  если C: X → Y, и  C(x) = A(x) + B(x) , ∀x∈X.

Оператор A действует из X в Y . Оператор C, действующий из X в Y, называется произведением оператора A на число α, если C(x) = α·A(x) для всех x из X :

A: X → Y,   C = α·A если C: X → Y, и  C(x) = α·A(x) , ∀x∈X.

Оператор A действует из X в Y, оператор B действует из Y в Z. Оператор C, действующий из X вZ, называетсяпроизведением операторов A и B, если C(x) = A(B(x) ) для всех x из X :

A: X → Y,  B: Y→Z,  C = B·A если C: X →Z, и  C(x) = B(A(x)) , ∀x∈X.

Сумма A + B линейных операторов, произведение линейного оператора на число α·A и произведениеB·Aлинейных операторов — линейные операторы.

Для операторов A + B , α·A и A·B , действующих в соответствующих пространствах, справедливо:

A + (B + C) = (A + B) + C;

α· (A + B) = α· A + α·B;

α· (B·A) =  (α·B) ·A;

(A·B)·C = A·(B·C);

(A + B)·C = A ·C+ B·C;

A·(B + C)= A·B + A·C;

A·I = I ·A.

50. Собственные векторы и собственные значения линейного оператора. Характеристический многочлен линейного оператора.

Собственные векторы и собственные значения линейного оператора      Ненулевой вектор   называется собственным вектором линейного оператора  , если  (  для комплексного  ), такое, что   Число   называется собственным числом (собственным значением) оператора f, соответствующим этому собственному вектору.

     Если в некотором базисе оператор f имеет матрицу А и в том же базисе вектор   имеет координатный столбец X, то   или 

     Собственные числа   линейного оператора   - корни характеристического уравнения  , где   - матрица оператора f,   - символ Кронекера.

     Для каждого собственного значения   соответствующие собственные векторы могут быть найдены из матричного уравнения   или соответствующей ему системы линейных уравнений

     Линейный оператор называется оператором простой структуры, если существует базис, состоящий из собственных векторов этого оператора. Матрица линейного оператора в этом базисе имеет вид

где   - соответствующие собственные значения.