AiG_voprosy_1
.docx
Матрица – математический объект, записываемый в виде прямоугольной таблицы, которая представляет собой совокупность строк и столбцов на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают её размерность.
Матрицы широко применяются в математике для компактной записи систем линейных уравнений. В этом случае количество строк матрицы соответствует числу уравнений, а количество столбцов количеству неизвестных. В результате решение Слау сводится к операциям над матрицами. Операции над матрицами: Сложение матриц, имеющих один и тот же размер. Сложение матрицы А+В есть операция нахождения матрицы С, все элементы которой равны попарной сумме всех соответствующих элементов матриц А и В, то есть каждый элемент матрицы С равен
Умножение матриц – есть операция вычисления матрицы С, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.
Транспонирование
матрицы – при транспонировании
матрицы, её строки заменяются столбцами,
а столбцы строками
|
Численная характеристика квадратной матрицы называется ее определителем. Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:
Для матрицы 2 на 2 детерминант определяется как:
Для матрицы определитель задаётся рекурсивно:
В частности, формула вычисления определителя матрицы 3 на 3 такова:
|
1). При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится. 2). Если две строки (столбца) матрицы совпадают, то её определитель равен нулю. 3). Если две или несколько строк (столбцов) матрицы линейно зависимы, то её определитель равен нулю 4). Общий множитель какого-либо ряда определителя можно вынести за знак определителя. 5). Если хотя бы одна строка (столбец) определителя нулевая, то определитель равен нулю. 6). Сумма произведений любой строки на их алг. Дополнения равна определителю. 7). Сумма произведений всех элементов любого ряда на алг. Дополнения соответствующих элементов параллельного ряда равна нулю. 8). Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей. 9). Определитель транспонированной матрицы равен определителю исходной.
|
a11a22a33 − a11a23a32 − a12a21a33 + a12a23a31 + a13a21a32 − a13a22a31
|
Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей. |
1). Найти определитель матрицы
2).
3).
4).
|
Обратной матрице А, называется такая матрица В, что при умножении А на В в результате получается единичная матрица. Для того чтобы найти обратную матрицу необходимо и достаточно, чтобы определитель исходной матрицы не равнялся нулю. Алгоритм нахождения обратной матрицы 1). Найти определитель матрицы, если он не равен нулю, то 2). К каждому из элементов исх. Матрицы найти их алг. Дополнения 3). Сформировать из алг. Дополнений матрицу и домножить её на 1\det результатом будет являться обратная матрица. |
1).
2).
3).
4).
5). Если необходимо решить систему линейных уравнений Ax=b (b-ненулевой
вектор), где x
– искомый вектор, и если
|
N – мерным вектором называется последовательность n чисел. Эти числа называются координатами вектора. Число координат вектора n называется размерностью вектора. Вектор записывается в виде строки или столбца:
Условие
равенства векторов: Два вектора
и Коллинеарные
векторы: Векторы А и В называются
коллинеарными если
Если > 0 то направления векторов совпадают Если < 0 то направления векторов противоположны Пример:
А и В коллинеарны и их направления совпадают т.к. = 2 > 0. Действия над векторами: Умножение вектора на число: любой n – мерный вектор А можно умножить на любое число , при этом все его координаты умножаться на это число. Сложение векторов: Два вектора одинаковой размерности можно сложить, при этом их соответствующие координаты складываются. Свойства линейных операций: А + В= В + А; (А+В)+С=А+(В+С); (А+В)= А+ В ( m)A= (mA) Скалярное произведение векторов: Скалярным произведение вектором называется число вычисляемое по формуле :
Свойства произведения: АВ=ВА (А+В)С=АС+ВС (АВ)= АВ Модуль (длина) вектора
Угол
между векторами
|
Определение линейной зависимости векторов Система
векторов А,А,А.А… называется линейно
зависимой, если существует ненулевой
набор чисел
Набор чисел является ненулевым если хотя бы одно из чисел лямбда отлично от нуля. Определение линейной зависимости: Система векторов является линейно зависимой при =0 |
Максимальная линейно независимая подсистема векторов – базис. Если все векторы подсистемы линейно независимы, а в любой вектор системы через них линейно выражается - В 0-ом пространстве базис не существует. -в 1-ом пространстве базис состоит из одного ненулевого вектора. -Во 2-ом пространстве – пара неколлинеарных векторов. -В 3-ем пространстве – упорядоченная тройка неколлинеарных векторов. |
Рангом матрицы А называется наибольший из порядков миноров матрицы А отличных от нуля. (Теорема) Ранг матрицы равен наибольшему числу линейно независимых строк (или столбцов) матрицы.
|
Теорема: Если в линейном пространстве есть базис из n векторов, то и любой другой базис состоит из n векторов. Определение: Линейное пространств, в котором существует базис из n векторов, называется n-мерным, а число n – размерностью пространства. Размерность пространства обозначается буквой& обозначается dim & В нулевом пространстве нет базиса, так как система из однородного нулевого вектора линейно зависима. Размерность нулевого пространства по определению считаем равной нулю. Может случиться такое, что каково бы ни было натуральное число m, в пространстве найдется m линейно независимых векторов. Такое пространство называется бесконечномерным. Базиса в нем не существует: если бы был базис из n векторов, то любая система из n+1 векторов была бы линейно зависимой по предложению 8 (если в линейном пространстве существует базис из n векторов, то любая система из m>n векторов линейно зависима) |
При вычислении ранга матрицы первым способом (способом окаймляющих миноров) следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D k-го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (k+1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен k. |
Ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы. Назовем элементарными преобразованиями матриц следующие действия над ними: 1) перестановка строк или столбцов; 2) умножение строки или столбца на число отличное от нуля; 3) добавление к одной из строк другой строки, умноженной на число или добавление к одному из столбцов другого столбца, умноженного на число. При элементарных преобразованиях ранг матрицы не меняется.
|
Теорема: Система уравнений совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы. Доказательство.
1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А®А* не изменяют ранга.
2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.
Доп к теореме: 1) Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение. 2) Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений. |
|
Однородная система всегда совместна, так как всегда имеется тривиальное решение.
Согласно общей теории, если r = n , то единственным является тривиальное решение.
Если же r < n, то решений бесконечно много, и все они, кроме одного, нетривиальные. Теорема: Однородная линейная система с квадратной матрицей имеет нетривиальное решение тогда и только тогда, когда определитель системы равен нулю. По теореме Крамера (5.1) detA=/0 тогда и только тогда, когда система с квадратной матрицей имеет единственное решение (т.е. векторы – столбцы системы (7.1) – линейно зависимы). В случае если задана система линейных однородных уравнений, это решение – тривиальное (0,0,…0). Значит, нетривиальные решения имеются тогда и только тогда, когда detA=0 (т.е. решений системы бесконечное множество). |
Всякая линейно независимая система (n-r) решений системы линейных однородных уравнений называется фундаментальной системой решений. Теорема: Однородная линейная система с квадратной матрицей имеет нетривиальное решение тогда и только тогда, когда определитель системы равен нулю. Док-во: По теореме Крамера (5.1) detA=/0 тогда и только тогда, когда система с квадратной матрицей имеет единственное решение (т.е. векторы – столбцы системы (7.1) – линейно зависимы). В случае если задана система линейных однородных уравнений, это решение – тривиальное (0,0,…0). Значит, нетривиальные решения имеются тогда и только тогда, когда detA=0 (т.е. решений системы бесконечное множество). |
Рассмотрим систему неоднородных уравнений
Ax = B (7.4) Пусть . rank A = rank A_ = r Пусть X0 – решение этой системы, т.е. AX0 = B (7.5)
Вычитая из (7.4) выражение (7.5), получим: A(X-X0) = 0 .
(X-X0) является решением соответствующего однородного уравнения.
Согласно (7.3) .
В нашем случае или (7.4).
Таким образом: Теорема 7.2
Общее решение представляется в виде суммы произвольного частного решения этой системы и общего решения соответствующей ей однородной системы. Следствие 1 Разность двух произвольных решений систем линейных неоднородных уравнений является решением соответствующей системы линейных однородных уравнений .
Следствие 2 Сумма любого частного решения системы линейных неоднородных уравнений с любым частным решением соответствующей системы линейных однородных уравнений дает частное решение системы линейных неоднородных уравнений . |
Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные |
Отрезок называется направленным, если указано какая из его граничных точек является началом, а какая концом. Основное соотношение: Рассмотрим на оси три точки О, М1, и М2 ОМ1+М1М2=ОМ2 Отрезок называется направленным, если указано какая из его граничных точек является началом, а какая концом. Если
известны координаты точек
То
Расстояние
между двумя точками на плоскости
определяется по формуле
|
Полярная система координат – двумерная система координат, в которой каждая точка на плоскости определяется двумя числами – это углом и расстоянием.
Полярная система координат особенно полезна в случаях, когда отношения между точками, проще изобразить в виде расстояний и углов, в более распространенной, декартовой или прямоугольной системе координат, такие отношения можно установить только путем применения тригонометрических уравнений.
Полярная система координат задается лучом, который называют нулевым (или полярной осью). Точка из которой он выходит называют началом координат или полюсом.
Любая точка на плоскости определяется двумя полярными координатами. Радиальной и угловой. Радиальная координата (обычно обозначается r) соответствует расстоянию от точки до начала координат. Угловая координата также называется полярным углом или азимутом и обозначается f(фи), равна углу, на который нужно повернуть против часовой стрелки полярную ось, чтобы попасть в эту точку.
Связь между полярными координатами и декартовыми.
Пару полярных координат r и f можно перевести в декартовы x и y путем применения тригонометрических формул X = r cos f Y= r sin f В то время как декартовы координаты x и y можно перевести в полярную координаты r
Для опрелеления угловой координаты f следует принять во внимание два следующих соображения 1). Для r = 0 , f может быть произвольным действительным числом 2). Для r =/ 0, чтобы получить уникальное значение f, следует ограничиться интервалом в 2п Обычно выбирают интервал [0,2п) или (-п, п] Для вычисления f в интервале [0,2п] Используют следующие уравнения
|
Свободный вектор – вектор, у которого известна длина и направление, но неизвестно положение в пространстве.
Проекция вектора на ось равна длине этого вектора, умноженной на косинус угла между вектором и осью
|
Зная координаты начала и координаты конца вектора, можно определить координаты самого вектора. Если точки заданы своими координатами А(x,y,z), B(x`,y`,z`), то AB(x`-x,y`-y,z`-z). Док-во: Очевидно соотношение OB=OA+AB откуда AB=OB-OA, так как по определению координаты точки совпадают с координатами её радиус вектора, то OB=(x,y,z) OA=(x`,y`,z) => AB=(x`-x,y`-y,z`-z);
Направляющие косинусы Углы, образуемые вектором а с координатными осями Ox Oy Oz определяются из формул
Косинусы определяемые по этим формулам называются направляющими Косинусами Для направляющих косинусов вектора имеет место формула
Т.е сумма квадратов косинусов углов образуемых вектором с тремя взаимно перпендикулярными осями, равна единице. |
Длина вектора – расстояние между началом и концом вектора. Расстояние между двумя точками пространства
|
Линейными операциями над векторами называются сложение векторов, и умножение вектора на число. Сложением двух векторов А и В называется такой вектор С. При этом складываются соответствующие координаты векторов А и В. Умножением вектора А на число m называется такой вектор С. При этом координаты этого вектора равны координатам вектора А умноженным на это число. |
1). Проекция суммы векторов на какую-нибудь ось равна сумме ее проекций на эту же ось. 2). При умножении вектора на число его проекция умножается на то же число.
|
Каким
бы ни был вектор
Коэффициент
этого разложения является координатами
вектора
|
Скалярным произведением векторов a и b и называют число, равное |a|*|b|*cos f , где — угол между векторами a и b. Обозначения: (a,b) или a*b .
Если один из векторов является нулевым, то несмотря на то, что угол f не определён, произведение равно нулю. Свойства скалярного произведения векторов: 1). Ab=ba 2). A(b+c)=ab+ac 3). K(a,b)=(ka,b) 4). (a,a)=|a|^2 Геометрически скалярное произведение есть произведение длины одного из сомножителей на ортогональную проекцию другого на направление первого (или наоборот). Скалярное произведение какого-то вектора A с единичным вектором есть ортогональная проекция вектора A на направление единичного вектора. |
Векторным произведением вектора a на вектор b называется вектор c, удовлетворяющий следующим требованиям: длина вектора c равна произведению длин векторов a и b на синус угла φ; между ними |c|=|a|*|b| sin f вектор c ортогонален каждому из векторов a и b вектор c направлен так, что тройка векторов abc является правой. Геометрически векторное произведение a на b есть ориентированная площадь параллелограмма, построенного на векторах , представленная псевдовектором, ортогональным этому параллелограмму. Свойства векторного произведения: 1). При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е 2). Векторное произведение обладает сочетательным свойством относительно скалярного множителя, то есть 3). Векторное произведение обладает распределительным свойством |
Смешанное произведение векторов (a,b,c) – это скалярное произведение вектора a на векторное произведение векторов b и c. Иногда смешанное произведение называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр). Геометрически смешанное произведение (a,b,c) есть (ориентированный) объем параллелепипеда, построенного на векторах .a,b и c. |
Общее уравнение прямой
Общее уравнение прямой линии на плоскости в декартовых координатах: Ax+By+C=0 где A, B и C — произвольные постоянные, причем постоянные A и B не равны нулю одновременно. Вектор с координатами (A,B) называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором.
При C = 0 прямая проходит через начало координат. Также уравнение можно переписать в виде : A(x-x0)+B(y-y0)=0 |
Уравнение прямой в отрезках
Прямая линия, пересекающая ось Ox в точке (а,0) и ось Oy в точке (0,b) :
В этом виде невозможно представить прямую, проходящую через начало координат. |
Нормальное
уравнение прямой где
p — длина перпендикуляра, опущенного
на прямую из начала координат, а θ —
угол (измеренный в положительном
направлении) между положительным
направлением оси Ox и направлением
этого перпендикуляра. Если p = 0, то
прямая проходит через начало координат,
а угол
Если прямая задана общим уравнением Ax + By + C = 0, то отрезки a и b, отсекаемые ею на осях, угловой коэффициент k, расстояние прямой от начала координат p, cosθ и sinθ выражаются через коэффициенты A, B и C следующим образом:
Во избежание неопределённости знак перед радикалом выбирается так, чтобы соблюдалось условие p > 0. В этом случае cosθ и sinθ являются направляющими косинусами положительной нормали прямой — перпендикуляра, опущенного из начала координат на прямую. Если C = 0, то прямая проходит через начало координат и выбор положительного направления произволен. |
Общее уравнение (полное) плоскости
где
A,B,C
и D
— постоянные, причём A.B
и C
одновременно не равны нулю; в векторной
форме: где r — радиус-вектор точки M(x,y,z), вектор N(A,B,C) перпендикулярен к плоскости (нормальный вектор). Направляющие косинусы вектора N:
Если один из коэффициентов в уравнении П. равен нулю, уравнение называется неполным. При D=0 П. проходит через начало координат, при A=0 (или B=0, C=0 ) П. параллельна оси Ox (соответствённо Oy или Oz). При A=B=0 (A=C=0, или B=C=0) П. параллельна плоскости Oxy (соответственно Oxz или Oyz). |
Уравнение плоскости в отрезках:
где a= -D/A , b= - D/B ,c= -D/C — отрезки, отсекаемые П. на осях Ox, Oy и Oz. |
Нормальное (нормированное) уравнение плоскости:
Расстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. Известно, что расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость. Расстояние
p
от точки M(x,y,z),
до плоскости, заданной уравнением
ax+by+cz+d=0,
вычисляется по формуле:
|
Каноническое уравнение получается из параметрическиx уравнений делением одного уравнения на другое:
Где ax,ay — координаты x и y направляющего вектора прямой, x0 и y0 координаты точки, принадлежащей прямой. |




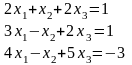 Решение
:
Решение
:
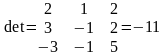


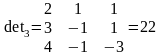

 ,
где (det)
– обозначает «определитель»
,
где (det)
– обозначает «определитель» - для любых двух обратимых матриц A
и B.
- для любых двух обратимых матриц A
и B. , где
, где
 обозначает транспонированную матрицу
обозначает транспонированную матрицу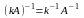 для
любого коэффициента
для
любого коэффициента

 существует, то
существует, то
 .
В противном случае либо размерность
пространства решений больше нуля,
либо их нет вовсе.
.
В противном случае либо размерность
пространства решений больше нуля,
либо их нет вовсе.

 равны
между собой если они имеют одинаковую
размерность и их соответствующие
координаты равны.
равны
между собой если они имеют одинаковую
размерность и их соответствующие
координаты равны.
 - некоторое число:
- некоторое число: и
и


 если вектор равен
1 то он называется единичным и
обозначается через
если вектор равен
1 то он называется единичным и
обозначается через

 или
или

 -
называется линейной комбинацией
векторов A1,A2,…,An
с коэффициентами
-
называется линейной комбинацией
векторов A1,A2,…,An
с коэффициентами

 при котором линейная комбинация
векторов равна ненулевому вектору,
то есть система уравнений имеет
ненулевое решение.
при котором линейная комбинация
векторов равна ненулевому вектору,
то есть система уравнений имеет
ненулевое решение.
 ,
,




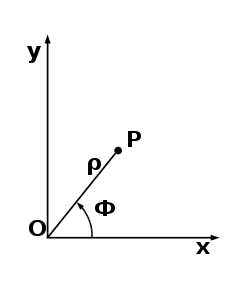
 (
по теореме Пифагора).
(
по теореме Пифагора).






 ,
он может быть разложен по азису i,
j,
k.
Т.е. может быть представлен в виде
,
он может быть разложен по азису i,
j,
k.
Т.е. может быть представлен в виде