5. Теорема сложения вероятностей.

Сформулируем и докажем для схемы случаев теорему сложения вероятностей.

Вероятность суммы несовместных событий равна сумме вероятностей этих событий, т.е.

P(A + B) = P(A) + P(B). (1)

Доказательство для схемы случаев. Пусть N — общее число элементарных событий. Считаем, что событиям A и B благоприятствуют M и K эле- ментарных события соответственно.

Согласно классическому определению вероятности в схеме случаев для вероятности событий A и B имеем:

. (2) P(A)=M\N ; P(B)=K\N

Поскольку события A и B несовместны, сумме этих событий благоприятствует M + K элементарных события. В этом случае, учитывая классическое определение вероятности, вероятность события A + B можно оценить по формуле:

. (3) P(A+B)=M+K\N

Подставляя (2), (3) в (1) получаем тождество, что и доказывает теорему сложения вероятностей для схемы случаев.

Теорема сложения вероятностей легко обобщается на случай несколь- ких несовместных событий A1, …, An. В этом случае имеем

.

Из формул (1), (1) легко вывести следующие два следствия.

Следствие №1. Если события A1, …, An образуют полную группу несовместных событий, то сумма их вероятностей равна единице, т.е.

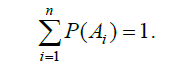
Следствие №2. Сумма вероятностей противоположных событий равна единице, т.е.

P(A)+P(вектор A)=1

6. Теорема умножения вероятностей

Вероятность события A, вычисленная при условии наступления другого

события B называется условной вероятностью события A и обозначается:

P(A|B). (1)

Учитывая обозначение (1), условие независимости событий A и B вы- глядит в виде:

P(A|B) = P(A). (2)

И, наоборот, события A и B зависят, когда

P(A|B) ≠ P(A). (2)

Теорема умножения вероятностей формулируется следующим образом.

Вероятность произведения пары событий равна произведению первого на условную вероятность второго, при условии, что первое событие имело место:

P(AB) = P(A)*P(B|A). (3)

Симметричное (3) выражение можно записать в виде:

P(AB) = P(B)*P(A|B). (3)

Часто используют следующие обозначения: P(A|B) = PB(A) = P(A)B.

Докажем теорему умножения вероятностей для схемы случаев. Пусть определены два события А, В, такие, что Р(А) ≠ 0 и P(B) ≠ 0, и пусть из всех возможных N исходов событию А благоприятствуют М исходов, событию В благоприятствуют К исходов, событию А и В благоприятствуют L исходов. Вероятности событий А, В, А·В соответственно равны Р(А) = M/N, Р(В) = K/N, Р(А·В) = L/N.

Подсчитаем условную вероятность события В|А. Событию В|А будут благоприятствовать L исходов из М исходов. Тогда Р(В|А) = = L/M. Разделим числитель и знаменатель дроби на N и получим

, (4) где Р(А) ≠ 0.

Вероятность наступления события В, вычисленная при условии, что событие А уже произошло, равна вероятности события АВ, деленной на вероятность события А. Из формулы (4) следует (3). Тем самым, теорема доказана.

7. Формула полной вероятности. Формула Бейеса.

2 Пусть требуется определить вероятность некоторого события A, которое может произойти вместе с одним из событий H1,…,HN, образующих полную группу несовместных событий. События H1,…,HN принято называть гипотезами.

Докажем, что верно следующее равенство:

т.е. вероятность события A вычисляется как сумма произведения вероятности каждой гипотезы на условную вероятность события A при выполнении дан- ной гипотезы.

Формула (19) называется формулой полной вероятности.

Доказательство. Поскольку гипотезы H1,…,HN образуют полную группу, постольку событие A может появиться вместе с одной из этих гипотез, т.е.

A = A*H1 + A*H2 + … + A*HN. (20)

Поскольку гипотезы H1,…,HN несовместны, постольку и произведения A*H1, …, A*HN также являются несовместными. По этой причине можно применить к (20) теорему сложения вероятностей, т.е.

. (21)

Применяя к произведениям A*Hi , i = 1,…,N теорему умножения вероятностей, получим формулу (19), что и требовалось доказать.

2

Следствием теоремы умножения вероятностей и формулы полной вероятности является так называемая теорема гипотез или формула Бейеса.

Пусть имеется полная группа несовместных гипотез H1,…,HN. Вероятность этих гипотез до опыта известна и равна P(H1), …, P(HN) (априорная вероятность). Пусть в результате опыта наступило событие A. Вопрос: как следует изменить вероятности гипотез H1,…,HN, чтобы учесть появление события A? Другими словами, в терминах условных вероятностей нас интересуют апостериорные вероятности P(H1|A), …, P(HN|A).

Из теоремы умножения вероятностей имеем

Выражая в (30) P(A) с помощью формулы полной вероятности, получим

Формулу (31) принято называть теоремой гипотез или формулой Бейеса.

8. Теоретико-множественная трактовка теории вероятностей

Основные понятия теории вероятностей могут быть истолкованы с точки зрения теории множеств, одного из самых абстрактных разделов математики.

Пусть U — множество возможных исходов некоторого испытания, опыта, эксперимента. Каждый элемент u множества U по определению назы-вается элементарным исходом, элементарным событием. В теории множеств принадлежность элемента u множеству U принято обозначать в виде: u  U. В этом случае множество U называется пространством элементарных исхо-дов или выборочным пространством.

9. Серии повторных опытов. Биномиальное распределение

На практике часто имеют дело с сериями опытов, испытаний, экспериментов, в которых условия проведения опытов могут не меняться, но могут и меняться. Точнее говоря, в зависимости от решения тех или иных задач, в некоторых случаях можно считать, что условия проведения опыта не изменились, в других случаях этого сказать нельзя. Конечно же, не существует двух одинаковых опытов. Изменения от опыта к опыту происходят всегда, хотя обнаружить эти изменения не всегда удается.

Пример №1. Рассмотрим стрельбу (рис.1,а) по мишени (рис.1,б). Когда имеет смысл говорить о неизменности условий стрельбы? До известной степени о неизменности условий опыта можно говорить, когда стрельба производится одиночными, прицельными выстрелами. При этом считается, что вся стрельба протекает в течение разумного времени, стрелок при этом не очень устает, погодные условия не слишком сильно меняются, оружие остается прежним, патроны используются одного и того же калибра и пр.

Как только стрелок пытается поразить мишень сериями выстрелов, говорить о независимости отдельных выстрелов уже нельзя. Выстрелы в серии связаны друг с другом.

Итак, в серии опытов может появиться или не появиться некоторое событие A. К классу задач под названием ―серия повторных опытов, ―повторные испытания, ―испытания Бернулли и пр. относят задачи вычисления вероятности наступления события A заданное количество раз. Эти задачи легко решаются, когда события независимы.

Испытания в серии считаются независимыми, если вероятность появление интересующего нас события не зависит от вероятности наступления этого события в других испытаниях серии.