8. Условная вероятность. Пример вычисления условной вероятности в классической схеме. Свойства условной вероятности.

Условной вероятностью Р(А|B) события А относительно события В, если Р(В) > 0, называется вероятность осуществления события А при условии, что событие В уже произошло. Условная вероятность определяется формулой Р(А|B) = (по определению) P(AB)/P(B). Рассмотрим опыт G, сводящийся к схеме случаев, и предположим, что событиям А, В, АВ благоприятствуют соответственно m_A, m_B > 0, m_AB случаев из всех n возможных. Допустим, что событие В уже произошло. Это означает, что из всех возможных n случаев реально могло появиться только m_B случаев, причем из них только m_AB случаев благоприятствуют событию А. Тогда Р(А|B) = m_AB/m_B.

P(AB)=P(A)P(B|A)=P(B)P(A|B). Свойства условной вероятности:

- Р(А|) = Р(А).

- Если события А и В несовместны, то Р(А|B)=0.

- Если события А и В независимы, то Р(А|B) = P(A). События независимы тогда и только тогда, когда условная вероятность совпадает с безусловной.

- Условная вероятность обладает всеми свойствами вероятности.

- Если В  А, то Р(А|B)=1.

Пример: Пусть опыт G состоит в подбрасывании монеты. Монету подбросили. В первый раз выпала решка. Какова вероятность того, что и во второй раз выпадет решка? Решение: Обозначим событие А (в первый раз выпала решка) и событие В (во второй раз выпала решка). Р(B|A)=P(AB)/P(A)=(1/4)/(1/2)=1/2. Обратим внимание, что Р(В|A)=P(B), что говорит о том, что события А и В независимы.

9. Полная группа гипотез. Формула полной вероятности. Пример.

События H₁, …, H_n в опыте G образуют полную группу несовместных событий, если они попарно несовместны (H_iH_j =  i  j) и в результате опыта произойдет хотя бы одно из событий H_i, i = 1,n, т.е. H₁+…+H_n=. События H₁, …, H_n называются гипотезами, если они образуют полную группу несовместных событий и Р(H_i) > 0, i = 1,n. Для полной группы событий характерно P(H₁) + … + P(H_n) = 1. Пусть с опытом G связаны гипотезы Н₁, …, Н_n. Тогда вероятность появления произвольного события А в опыте G выражается формулой полной вероятности:

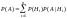
Формула полной вероятности позволяет выразить вероятность сложного события А через вероятности составляющих его более простых событий АH_i, i=1,n. Данная формула используется в опытах, не сводящихся к схеме случаев. Пример: В торговую фирму поступают телевизоры от трёх фирм изготовителей в соотношении 2:5:3. Телевизоры, поступающие от первой фирмы, требуют ремонта в течение гарантийного срока в 15% случаев, от второй и третьей – соответственно в 8% и 6% случаев. Найти вероятность того, что проданный телевизор потребует ремонта в течение гарантийного срока. Решение: Событие А заключается в том, что проданный телевизор потребовал гарантийного ремонта. Введем гипотезы: H₁ - телевизор изготовлен первой фирмой, Н₂ и Н₃. Вероятности этих гипотез 0,2, 0,5 и 0,3 соответственно. Условные вероятности тоже известны. P(A|H₁) = 0,15; P(A|H₂)=0,08; P(A|H₃)=0,06. По формуле полной вероятности P(A) = 0,20,15 + 0,50,08 + 0,30,06 = 0,088.

10. Формула умножения. Формула Байеса. Примеры.

Вероятность одновременного появления событий A1, …, An выражается формулой умножения вероятностей: P(A₁A₂…A_n)=P(A₁)P(A₂|A₁)…P(A_n|A₁…A_n-1), в которой вероятность каждого следующего по порядку события вычисляется при условии, что в рассматриваемом опыте произошли все предыдущие события. Пусть с опытом G связаны гипотезы H₁, …, H_n. Предположим, что при проведении опыта произошло событие А, вероятность которого была Р(А) > 0. Пусть до опыта G были известны лишь априорные вероятности гипотез Р(H_i), i=1,n, и соответствующие им условные вероятности события А. В этом случае условная вероятность P(H_i|A) гипотезы Hi при условии, что событие А произошло, вычисляется по формуле Байеса:

Даная формула вытекает из свойств условной вероятности. Рассмотрим пример: После осмотра больного врач считает, что равновозможно одно из двух заболеваний С или D. Для уточнения диагноза больного направляют на анализ, исход которого дает положительную реакцию при заболевании C в 30% случаев, а при заболевании D – 20% случаев. Анализ дал положительную реакцию. Какое заболевание становится более вероятным? Решение: Событие А заключается в том, что анализ дал положительную реакцию. Гипотезы H₁ и Н₂ заключаются в том, что пациент болен заболеванием C или D соответственно. P(H₁) = P(H₂) = 0,5. P(A|H₁) = 0,3; P(A|H₂) = 0,2. Найдем полную вероятность.

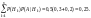
Р(H₁|A)=0,15/0,25=0,6; P(H₂|A)=0,1/0,25=0,4. Более вероятно заболевание C.

11. Случайные величины. Закон распределения случайной величины. Дискретные случайные величины: ряд распределения и его свойства. Непрерывные случайные величины: функция плотности и ее свойства. Вероятность попадания случайной величины в множество.

Случайной величиной (СВ) Х() называется функция элементарного события  такая, что событие {: X()  x} принадлежит -алгебре F при любом действительном x. Значения x функции Х() называются реализациями СВ Х(). Законом распределения случайной величины называется любое правило (таблица, функция), позволяющее находить вероятности всех возможных событий, связанных с СВ. СВ называется дискретной, если множество ее возможных значений конечно или счетно. Простейшей формой закона распределения дискретной СВ с конечным множеством значений является ряд распределения p_k = (по определению) P{X = x_k}, k=0,n, который задается аналитически или таблицей. В полученном ряду распределения сумма всех вероятностей равна единице. СВ Х с непрерывной функцией распределения F_x(x) называется непрерывной. Плотностью распределения (плотностью вероятности) СВ Х называется неотрицательная кусочно-непрерывная функция f_x(x), для которой при любом x  R¹ выполняется соотношение:

Свойства f_x(x):

- f(x)  0 для всех x  R¹, т.е. выполняется условие неотрицательности плотности.

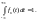- (Условие нормировки плотности).

-

- F`(x)=f(x) в точках непрерывности плотности f(x).

12. Функция распределения случайной величины и ее свойства. Вероятность попадания случайной величины в промежуток. Связь функции распределения с плотностью вероятности (в непрерывном случае).

Функция распределения F(x) является одной из форм закона распределения для СВ всех типов и однозначно определяет СВ.

Свойства F(x):

- F(x) определена для всех x  R¹.

- 0  F(x)  1 для всех x  R¹.

- F(-) = 0; F() = 1.

- F(х₂) – F(х₁) = Р{х₁ < Х  х₂}, если х₂ > х₁.

- F(x) не убывает.

- Если F(x) непрерывна, то F(х₂) – F(х₁) = Р{х₁  Х  х₂}.

- F`(x)=f(x) в точках непрерывности плотности f(x).

13. Квантиль и медиана случайной величины. Медиана симметричного распределения. Пример нахождения квантили нормальной случайной величины.

Квантилью уровня p функции распределения F(x) СВ Х называется минимальное значение x_p, при котором функция распределения F(x) не меньше значения p, где p  (0,1). Если функция распределения строго монотонна и непрерывна, то квантиль является единственным решением уравнения F(x_p) = p. Квантиль уровня p = ½ называется медианой. Если плотность распределения существует, симметрична относительно оси Оу и строго положительна на связном множестве (отрезке или оси Ох), то х_р = -х_1-р. Пример нахождения квантили нормальной СВ: Для нормальной случайной величины функция распределения F(X) = Ф((x-m)/) = ½ + Ф₀((x-m)/). Для функции Ф₀ (функции Лапласа) имеется таблица значений. Найдем квантиль уровня ¾. Для этого найдем решение уравнения F(x_p) = ¾. Ф₀((x-m)/) = ¼. Воспользовавшись таблицей значений функции Лапласа получаем, что ((x-m)/)  0,675. Для стандартной нормальной СВ, у которой m=0 и ²=1 полученное значение 0,675 является квантилью уровня ¾.

Квантили стандартного нормального распределения:

р	Квантиль уровня р
0,01		-2,326348
0,025		-1,959964
0,05		-1,644854
0,1		-1,281552
0,3		-0,524401
0,4		-0,253347
0,5		0
0,6		0,253347
0,7		0,524401
0,8		0,841621
0,9		1,281552
0,95		1,644854
0,975		1,959964
0,99		2,326348