Библиотека 5баллов.ru Соглашение об использовании Материалы данного файла могут быть использованы без ограничений для написания собственных работ с целью последующей сдачи в учебных заведениях. Во всех остальных случаях полное или частичное воспроизведение, размножение или распространение материалов данного файла допускается только с письменного разрешения администрации проекта www.5ballov.ru.  РосБизнесКонсалтинг

1. Понятие случайности, изучаемое теорией вероятностей. Частотное определение вероятности.

Теория вероятностей – раздел математики, изучающий закономерности случайных явлений, наблюдаемых при многократном повторении опыта. Под опытом G понимается воспроизведение какого-либо комплекса условий для наблюдения исследуемого явления (события). Обычно считается, что событие случайно в опыте, если при неоднократном воспроизведении этого опыта оно иногда происходит, а иногда – нет, причем нельзя заранее предсказать возможный исход (событие) этого опыта. При этом наблюдается свойство устойчивости частоты случайного события: с увеличением числа повторений опыта значение частоты появления случайного события стабилизируется около некоторого случайного числа. Пусть при n-кратном повторении опыта G событие А произошло m_А раз. Частотой W_n(А) события А называется соотношение W_n(A) = m_А/n. Cвойства частоты W_n(А):

- W_n(А)  0, так как m_А  0 и n > 0;

- W_n(А)  1, так как m_А  n;

- Если при n-кратном повторении опыта несовместные события A и B появились соответственно m_А и m_B раз, то

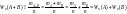
Априори (заранее, до опыта) частота W_n(A) является случайной, т.е. нельзя предсказать точное ее значение до проведения данной серии из n опытов. Однако природа случайных событий такова, что на практике наблюдается эффект устойчивости частот. Его суть заключается в том, что при увеличении числа опытов значение частоты практически перестает быть случайным и стабилизируется около некоторого неслучайного числа Р(А), соответствующего данному конкретному событию А в опыте G. Число Р(А) первоначально при становлении теории вероятностей называлось вероятностью события A в опыте G. Введенное понятие указывает на то, что вероятность Р(А) характеризует частоту появления события А при многократном повторении опыта G.

2. Основные понятия теории вероятностей на основе аксиоматического подхода: пространство элементарных исходов, алгебра случайных событий, вероятность и аксиомы, которым она подчиняется.

Алгебра событий F, включающая в себя результаты сложения и умножения счетного числа своих элементов (т.е. замкнутая относительно этих операций), называется -алгеброй. Элементы -алгебры (т.е. подмножества пространства ) называются случайными событиями (или просто событиями). Вероятностью события А называется числовая функция Р(А), определенная на -алгебре и удовлетворяющая следующим четырем аксиомам теории вероятностей:

- Каждому событию А  F ставится в соответствие неотрицательное число Р(А), т. е. Р(А)  0 для любого А  F.

- Вероятность достоверного события равна единице, т. е. Р() = 1.

- Для любых несовместных событий А и В из F справедливо равенство Р(А + В) = Р(А) + Р(В).

- Для любой убывающей последовательности А₁  А₂  …  А_n  … событий из F, такой что A₁A₂A₃  ...  A_n  …=  , имеет место равенство

Аксиоматические свойства вероятности:

- Если Р(А) = 1, но А не равно , то говорят, что событие А в опыте G происходит почти наверное.

- Если Р(А) = 0, то говорят, что событие А почти никогда не происходит в опыте G.

3. Простейшие свойства вероятности: монотонность, формула сложения, вероятность разности событий.

Если А  В, то Р(А)  Р(В), т.е. вероятность монотонна. Представим множество В как В = А + B\A (см. рисунок 1). По построению А(В\А)=, следовательно, события А и В\А несовместны. Поэтому по аксиомам конечной аддитивности^* и неотрицательности вероятности имеем Р(В) = Р(А) + Р(В\А)  Р(А).

Р(А)  1 для любого А  F. Так как A  , то из свойства монотонности и аксиомы нормировки вероятности следует Р(А)  Р() = 1. Формула сложения и вероятность разности событий:

Р(А+В) = Р(А) + Р(В) – Р(АВ) для любых А, В  F. Представим А в виде А = А\В + АВ (см. рисунок 2). Очевидно, что события А\В и АВ несовместны. Тогда по аксиоме конечной аддитивности вероятности имеем Р(А) = Р(А\В) + Р(АВ),откуда Р(А\В)=Р(А)-Р(АВ). Аналогичным образом поступим с событием А+В. Имеем А+В = В + А\В, причем события В и А\В несовместны. Тогда из аксиомы конечной аддитивности вероятности следует Р(А+В)=Р(В)+Р(А\В). Подставляя в данное выражение формулу для Р(А\В), получаем требуемое. Р(А+В)=Р(А)+Р(В)-Р(АВ).

^* Аксиома: Для любых несовместных событий А и В из F справедливо равенство Р(А + В) = Р(А) + Р(В).