Міністерство освіти України

Інститут змісту і методів навчання

Вінницький державний технічний університет

С.Г.Авдєєв

ЗБІРНИК ЗАДАЧ З ФІЗИКИ

ЧАСТИНА 2

(коливання і хвилі, хвильова та квантова оптика)

Міністерство освіти України

Інститут змісту і методів навчання

Вінницький державний технічний університет

ISBN 5 - 7763 - 8728 - 0

С.Г.Авдєєв

Збірник задач з фізики

ЧАСТИНА 2

(коливання і хвилі, хвильова та квантова оптика)

Навчальний посібник для студентів технічних спеціальностей вищих навчальних закладів

Рекомендовано міністерством освіти України

ВІННИЦЯ 1997

УДК 530,1(075.8)

Авдєєв С.Г. Збірник задач з фізики. Частина 2, (коливання і хвилі, хвильова та квантова оптика);

Навчальний посібник /В. ВДТУ,: 1997 - 150 с. Укр. мовою/.

Посібник охоплює розділи “Коливання і хвилі” і “Хвильова та квантова оптика”, які традиційно викладаються в одному семестрі. Кожен розділ супроводжується невеликими теоретичними викладками у вигляді законів і формул, а також прикладами розв’язування задач.

Посібник складено у відповідності з діючою програмою курсу фізики в технічних вузах з можливістю широкого залучення творчої самостійної роботи студентів при плануванні і проведенні практичних занять.

Іл. 18. Табл. 4.Бібліогр.: 11 назв.

Рецензенти: П.М. Зузяк, доктор ф.м.н., професор

О.Г. Бунтар, доктор ф.м.н., професор

ISBN 5 - 7763 - 8728 - 0  C.Авдєєв,1997

МЕХАНІЧНІ КОЛИВАННЯ

Основні формули

1. Зміщення, швидкість і прискорення матеріальної точки при гармонічних коливаннях визначаються рівняннями:

х = А cos ( t + ₀),

v = - A  sin (t + ₀),

a = - A ²cos (t + ₀) = - ² x,

де А - амплітуда коливань,  - циклічна частота, ₀ - початкова фаза коливань.

2. Зв’язок циклічної частоти  з періодом коливань Т і частотою :

 = = 2  .

3. Сила, яка діє на тіло при вільних гармонічних коливаннях (квазіпружна сила):

F = ma = - m ² x = - k x,

де k = m² - коефіцієнт квазіпружної сили, який вимірюється силою, що визиває зміщення х = 1.

4. Кінетична, потенціальна і повна енергії гармонічних коливань матеріальної точки:

,

,

.

5. Диференціальні рівняння малих коливань:

а) математичний маятник

a+ x=0, де , звідки T = 2 ;

б) пружинний маятник

a+ x=0, де , звідки Т = 2 ;

в) фізичний маятник

a+ x = 0, де , звідки T = 2 ,

де І - момент інерції маятника відносно осі коливань; l - відстань від осі коливань до центра мас маятника.

При відсутності опору середовища циклічна частота коливань  називається власною циклічною частотою і позначається через ₀.

6. При додаванні двох однаково направлених гармонічних коливань однакового періоду одержуємо гармонічне коливання того ж періоду, амплітуда якого А і початкова фаза ₀ визначаються рівняннями:

,

tq ₀ = ,

де А₁ і А₂ - амплітуди коливань, що складаються; ₁ і ₂ - початкові фази цих коливань.

7. При додаванні двох однаково направлених гармонічних коливань однакової амплітуди і близьких частот (₁  ₂) одержуємо биття, яке описується рівнянням:

x = cos ,

де - амплітуда биття.

Періодичність зміни амплітуди визначається періодичністю зміни модуля косинуса, тому період биття дорівнює:

T_б =  , звідки T_б = .

8. При додаванні двох взаємно перпендикулярних гармонічних коливань з однаковою частотою в напрямі координатних осей х і у матимемо рівняння траєкторії результуючого руху матеріальної точки:

cos(₂ - ₁) = sin² (_{2 -} ₁),

де А₁ і А₂ - амплітуди коливань, що додаються; _{2 -} ₁ - різниця фаз цих коливань.

9. Диференціальне рівняння затухаючих коливань :

0, або a+2 x+ x =0,

де  = - коефіцієнт затухання; r - коефіцієнт опору середовища; - власна циклічна частота коливань.

10. Загальний розв’язок диференціального рівняння для затухаючих коливань має вигляд:

x = A₀e^-t cos (t + ),

де А₀е^-t - амплітуда затухаючих коливань;  - циклічна частота затухаючих коливань.

11. Швидкість зменшення амплітуди затухаючих коливань характеризують логарифмічним декрементом затухання

 = ln ,

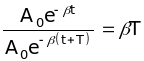де  - логарифмічний декремент затухання;  - коефіцієнт затухання; Т - період затухаючих коливань.

12. Циклічна частота затухаючих коливань

 = , або  = .

13. Період затухаючих коливань:

T = , або Т = .

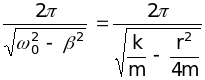14. Добротність коливальних систем

 = 2 , або  = ,

де W_t - повна енергія, яку має коливальна система на момент часу t;

W_(t+T) - втрати енергії коливальної системи за один період;  - логарифмічний декремент затухання;  - коефіцієнт затухання; ₀ - власна частота коливань; Т - період затухаючих коливань (при малих затуханнях Т  Т₀).

15. Диференціальне рівняння вимушених коливань

,

або

де F₀ - змушувальна сила;  - циклічна частота вимушених коливань.

16. Загальний розв’язок диференціального рівняння вимушених коливань, які протягом певного часу встановлюються під дією змушувальної сили має вигляд:

x = A cos (t + )

де А - амплітуда вимушених коливань;  - зсув за фазою вимушених коливань і змушувальної сили.

17. Амплітуда вимушених коливань

A = ,

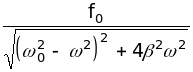де f₀ = ; ₀ - власна частота коливань системи;  - циклічна частота змушувальної сили.

18. Зсув фази вимушених коливань:

tg = - .

19. Резонансна частота і резонансна амплітуда:

_рез = ;

А_рез = .