43. Каноническое уравнение эллипсоида

Общий вид

Свойства

Эллипсоид – ограниченная поверхность, поскольку из его уравнения следует, что     

Эллипсоид обладает

• центральной симметрией относительно начала координат,

• осевой симметрией относительно координатных осей,

• плоскостной симметрией относительно начала координат.

В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается эллипс.

44. Каноническое уравнение

Общий вид

Свойства

Однополостный гиперболоид - неограниченная поверхность, так как из его канонического уравнения слудует, что Z (-∞;+∞)

Однополостный гипербалоид обладает

- центральной симметрией относительно начала координат

- осевой симметрией относительно всех координатных осей

- плоскостной симметрией относительно всех координатных плоскостей

В сечении однополостного гиперболоида плоскостью, ортогональной оси Oz, получается эллипс , а плоскостями, ортогональными осям Ox и Oy – гипербола.

45. Каноническое уравнение двуполостного гиперболоида

Общий вид

Свойства

Двуполостный гиперболоид неограниченная поверхность , поскольку из его канонического уравнения следует, что и не ограничен сверху.

Двуполостный гиперболоид обладает

-центральной симметрией относительно начала координат

-осевой симметрией относительно всех координатных осей

-симметрией относительно всех координатных плоскостей

В сечении двуполостного гиперболоида плоскостью, ортогональной оси координат Ох, при

Получается эллипс, а плоскостями ортогональными осям Оy и Oz – гипербола.

46.

Уравение:  Общий вид: Основное свойство конуса: если точка M0(x0, y0, z0) лежит на конусе второго порядка, то и вся прямая OM0 также лежит на нем, где O - вершина конуса, точка M0 отлична от вершины конуса. 47. 

Координатные плоскости Оyz и OXZ являются плоскостями симметрии: при замене х на - х, у на - у уравнение не меняется. Поверхность проходит через начало координат и расположена над плоскостью Оху, так как z ≥ 0.  При сечениях z = h получаются эллипсы ,полуоси которых , растут с ростом h. При сечении плоскостями х = 0 и у = 0 получаются параболы , 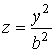, точки которых являются вершинами указанных выше эллипсов. При a=b параболы становятся равными, эллипсы обращаются в окружности и параболоид становится поверхностью порождаемой вращением параболы около ее оси (параболоид вращения). 48. 

Координатные плоскости Оyz и OXZ являются плоскостями симметрии: при замене х на − х, у на − у уравнение не меняется.  При сечении поверхности плоскостью х = 0 в сечении получается парабола  При сечении поверхности плоскостью у = 0 в сечении получается парабола  . При сечении поверхности плоскостью z = 0 в сечении получается пара пересекающихся прямых  Сечение плоскостями z = h даёт гиперболы с уравнениями  При h > 0 ветви гипербол расположены вдоль оси Ох, при h < 0 ветви гипербол расположены вдоль оси Оу. 49.

Цилиндрической поверхностью называется поверхность, полученная движением прямой (образующей), перемещающейся параллельно некоторому вектору и пересекающей во время движения фиксированную линию (направляющую). Уравнение F(x, y) = 0 определяет цилиндрическую поверхность с образующей параллельной оси Oz.  Уравнение определяет эллиптический цилиндр.   Уравнение определяет гиперболический цилиндр.  Уравнение определяет параболический цилиндр.  50.

Часто приходится встречаться с объектами, над которыми производятся операции сложения и умножения на числа. Приведем несколько примеров.  1. В геометрии объектами такого рода являются векторы в трехмерном пространстве, т.е. направленные отрезки 2. В алгебре мы встречаемся с системами чисел (например, строки матрицы, совокупность коэффициентов линейной формы и т.д.).  3. В анализе определяются операции сложения функций и умножения их на числа.  В приведенных примерах одни и те же операции сложения и умножения на числа производятся над совершенно разными объектами. Для того чтобы изучить все такие примеры с единой точки зрения, мы введем понятие линейного, или аффинного, пространства.  Пусть М- множество элементов произвольной природы, для которых определены операции сложения и умножения на действительное число:  паре элементов множества , отвечает элемент , называемый суммой и ;  паре , отвечает элемент , называемый произведением числа и элемента .  Будем называть множество M линейным пространством, если для всех его элементов определены операции сложения и умножения на действительное число и для любых элементов и произвольных чисел справедливо:  1. , сложение коммутативно;  2. , сложение ассоциативно;  3. существует единственный нулевой элемент такой, что , ;  4. для каждого элемента существует единственный противоположный элемент такой, что ,  5. , умножение на число ассоциативно;  6. , ;  7. , умножение на число дистрибутивно относительно сложения элементов;  8. , умножение вектора на число дистрибутивно относительно сложения чисел.  Пусть — линейное пространство. Векторы называются линейно зависимыми, если существуют такие числа , из которых хотя бы одно отлично от нуля, что  Линейное пространство называется n-мерным, если в нем существует n линейно независимых векторов и нет большего числа линейно независимых векторов. Линейные пространства X и Y называются изоморфными, если между их элементами можно установить такое взаимно однозначное соответствие, что если векторам X и X’ из X соответствуют векторы Y и Y’ из Y, то вектору X+X’ соответствует вектор Y+Y’ и при любом вектору соответствует вектор . 51. Совокупность n линейно независимых векторов -мерного пространства называется базисом в  Теорема. Каждый вектор из n-мерного пространства можно представить, и при том единственным образом, как линейную комбинацию векторов базиса. 52. Пусть и — два базиса n-мерного пространства. Пусть, далее, каждый вектор выражается через векторы первого базиса формулами

  Тогда переход от первого базиса ко второму задается матрицей , определитель которой отличен от нуля .  Обозначим через координаты вектора x в первом базисе, а через — его координаты во втором базисе. Найдем, как выражаются координаты через .  Мы имеем: 

Подставив в это равенство вместо их выражения через , получим: 

Так как линейно независимы, то коэффициенты при них в правой и левой частях равенства одинаковы. Получаем: 

Сравним формулы (16) и (17). Между ними есть два существенных отличия: во-первых, поменялись местами штрихованные и нештрихованные буквы и, во-вторых, в формулах (16) при суммировании меняется первый индекс, а в формулах (17) второй.  Таким образом, координаты вектора x в первом базисе выражаются через координаты того же вектора x во втором базисе с помощью матрицы , транспонированной к . 

53.

Будем говорить, что в вещественном пространстве определено скалярное произведение, если каждой паре векторов поставлено в соответствие действительное число, которое обозначим через причем это соответствие обладает следующими свойствами (удовлетворяет следующим аксиомам):

1 , т.е. скалярное произведение симметрично.  2 , где — действительное число.  3 (дистрибутивность скалярного произведения).  4 Скалярное произведение вектора с самим собой неотрицательно: , и обращается в нуль, лишь если .  Аффинное пространство, в котором определено скалярное произведение, удовлетворяющее условиям 1 -4 , мы называем евклидовым. Число называется длиной векторa X ;  число — расстоянием между векторами X Y;  угол , косинус которого , — углом между векторами X, Y, , .  Свойства скалярного произведения:. - коммутативность - линейность - линейность и - невырожденность Неравенство Коши--Буняковского (6) Чтобы доказать его, рассмотрим вектор , где t — произвольное действительное число. Согласно аксиоме 4 скалярного произведения  т.е. для любого t Мы видим, что стоящий слева квадратный относительно t трехчлен принимает лишь неотрицательные значения. Следовательно, дискриминант уравнения 

не может быть положительным, т.е.  что и требовалось доказать.