28.Разложение векторов на компоненты.

Если и — два неколлинеарных вектора в плоскости, а — произвольный вектор в той же плоскости, то всегда существуют такие числа и , что . В этом случае говорят, что вектор разложен по векторам .

Если — неколлинеарные единичные векторы (т. е. вектора, модуль которых равен единице) , , то произвольный вектор плоскости может быть представлен в виде . В этом случае говорят, что вектор имеет в системе и координаты .

Если векторы взаимно перпендикулярны, причем вектор может быть получен из вектора поворотом против часовой стрелки, то говорят, что прямые, в которых лежат , образуют декартову прямоугольную систему координат, а числа называются декартовыми координатами вектора .

29.Скалярное произведение векторов и их свойства.

30.Векторное произведение векторов и их свойства.

Три некомпланарных вектора a, b и с, взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора с кратчайший поворот от первого вектора а ко второму вектору b виден совершающимся против часовой стрелки, и левую, если по часовой (см. рис. 16).

Векторным произведением вектора а на вектор b называется вектор с, который:

1. Перпендикулярен векторам a и b, т. е. с^а и с^b;

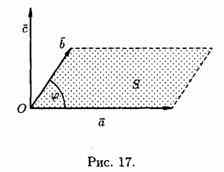
2. Имеет длину, численно равную площади параллелограмма, построенного на векторах а и b как на сторонах (см. рис. 17), т. е.

3.Векторы a, b и с образуют правую тройку.

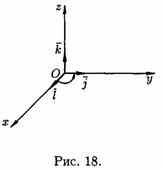
Векторное произведение обозначается а х b или [а,b]. Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами i , j и k (см. рис. 18):

i х j = k, j х k = i, k х i = j.

Докажем, например, что iхj=k.

1) k^i, k^j;

2) |k|=1, но | i * j| = |i| • |J| • sin(90°)=1;

3) векторы i , j и k образуют правую тройку (см. рис. 16).

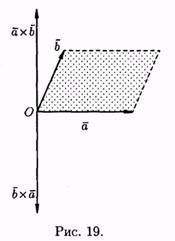
1. При перестановке сомножителей векторное произведение меняет знак, т.е. а хb =(b хa ) (см. рис. 19). Векторы ахb и b ха коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены (тройки а , b , а * b и a , b , b*a противоположной ориентации). Стало быть a*b = -(b*a ). 2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. 1(а *b ) = (1а ) * b = а * (1b ).

Пусть l>0. Вектор l(ахb ) перпендикулярен векторам а и b . Вектор ( lа)хb также перпендикулярен векторам а и b (векторы а, lа лежат в одной плоскости). Значит, векторы l(ахb ) и ( lа)хb коллинеарны. Очевидно, что и направления их совпадают. Имеют одинаковую длину:

Поэтому 1(a хb )= 1ахb . Аналогично доказывается при 1<0.

3. Два ненулевых вектора а и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е. а||b <=>ахb =0.

В частности, i *i =j *j =k *k =0.

4. Векторное произведение обладает распределительным свойством:

(a+b) *с= а*с+b * с.

31. Смешанное произведение векторов. Свойства

Сме́шанное произведе́ние   векторов   — скалярное произведение вектора   на векторное произведение векторов   и  :

.

Свойства: :

• Если какие-то два вектора коллинеарны, то с любым третьим вектором они образуют смешанное произведение, равное нулю.

• Если три вектора . компланарны, лежат в одной плоскости(линейно зависимы ), то их смешанное произведение равно нулю.

• Геометрический смысл — Смешанное произведение   по абсолютному значению равно объёму параллелепипеда , образованного векторами   и  ; знак зависит от того, является ли эта тройка векторов правой или левой.