23.Понятие свободного вектора. Теорема о проекции вектора на ось.

Своодные векторы -  векторы, которые коллинеарны, одинаково направлены и имеют одинаковые длины.

Теорема о проекции вектора на ось:  проекция вектора на ось равна длине этого вектора, умноженной на косинус угла между векторами и осью.

Проекция суммы двух векторов на ось равна сумме проекций векторов на ту же ось.

.

Если вектор умножается на число , то его проекция на ось также умножается на это число.

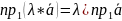
Следствие: равные вектора имеют равные проекции на одну ось.

24.Координаты вектора и их вычисление по координатам его начала и конца. Направляющие косинусы.

координаты вектора 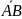  равны разности соответствующих координат точек его конца и начала, то есть, на плоскости , а в трехмерном пространстве  .

Направляющие косинусы - это косинусы углов, которые вектор образует с положительными полуосями координат. Направляющие косинусы однозначно задают направление вектора.

.

25.Длина вектора и формула для вычисления расстояния между двумя точками пространства.

Длина вектора  обозначается как  и называется модулем вектора.

Если на плоскости заданы точки и 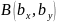, то его длина вычисляется по формуле(следствие из теоремы Пифагора):

.

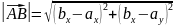26.Линейные операции над векторами.

Суммой двух векторов называется вектор, который идет из начала вектора в конец вектора при условии, что вектор приложен к концу вектора (правило треугольника).

Наряду с правилом треугольника часто пользуются (равносильным ему) правилом параллелограмма: если векторы приведены к общему началу и на них построен параллелограмм, то сумма есть вектор, совпадающий с диагональю этого параллелограмма, идущей из общего начала . Отсюда сразу следует, что .

Разность двух векторов называется вектор, который в сумме с вектором составляет вектор . Если два вектора приведены к общему началу, то разность их 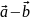есть вектор, идущий из конца («вычитаемого») к концу («уменьшаемого»). Два вектора равной длины, лежащие на одной прямой и направленные в противоположные стороны, называются взаимно обратными: если один из них обозначен символом , то другой обозначается символом 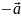. Легко видеть, что . Таким образом, построение разности равносильно прибавлению к «уменьшаемому» вектора, обратного «вычитаемого».

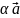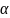Произведение вектора на число называется вектор, модуль которого равен произведению модуля вектора на модуль числа ; он параллелен вектору или лежит с ним на одной прямой и направлен так же, как вектор , если - число положительное, и противоположно вектору , если - число отрицательное.

Сложение векторов и умножение вектора на число называются линейными операциями над векторами.

27.Основные теоремы о проекциях векторов.

Теорема 1. Проекция суммы векторов на какую-либо ось равна сумме проекций слагаемых векторов на ту же ось.

Теорема справедлива при обоих смыслах термина “проекция вектора” и при любом числе слагаемых; так, при трёх слагаемых:

Пр(а1+а2+а3)=Пра1+Пра2+Пра3 (1)

пр(а1+а2+а3)=пра1+пра2+пра3. (2)

Формула (1) вытекает из определения сложения векторов, формула(2)-из правила сложения положительных и отрицательных чисел.

Теорема 2. Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:

.
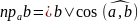