15. Вычисление ранга матрицы методом элементарных преобразований.
Ранг канонической матрицы равен числу единиц на главной диагонали. На этом основан способ вычисления матрицы методом элементарных преобразований.
Пример. Найти ранг матрицы
А =
~
~
~
~
~
~
~
Таким образом, ранг матрицы А равен r(A) = 2.
16. Теорема Кронекера-Капелли. Решение систем на основе теоремы Кронекера-Капелли.
Теорема. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.
Пример. Определить
совместность системы линейных уравнений:
A
= 
~ 
. 
RgA
= 2.
A* = 
RgA*
= 3.
17. Однородная система линейных уравнений. Свойства её решений.
Однородная
система всегда совместна (r(A)
= r(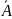
)),
она имеет нулевое(тривиальное) решение
х1
= х2
= … = хn
= 0.
Условия, при которых однородная система имеет ненулевые решения:
Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг r её основной матрицы был меньше числа n неизвестных, т.е. r < n.
Для того, чтобы однородная система n линейных уравнений с n неизвестными имела ненулевые решения, необходимо и достаточно, чтобы её определитель Δ был равен нулю, т.е. Δ = 0.
18. Фундаментальная система решений однородной системы линейных уравнений и теорема о числе решения в её составе.
Совокупность решений системы линейных однородных уравнений называется фундаментальной системой решений, если эта совокупность состоит из линейно независимых решений и любое решение системы является линейной комбинацией этих решений.
Теорема. Если ранг r матрицы системы меньше числа n неизвестных, то существует фундаментальная система решений, состоящая из (n-r) решений.
19. Связь решений линейной неоднородной и соответствующей ей однородной систем.
Сумма любого решения неоднородной системы и любого решения соответствующей однородной системы является решением неоднородной системы.
Разность любых двух решений неоднородной системы является решением соответствующей однородной системы.
20. Метод Гаусса решения линейных уравнений.
Метод Гаусса состоит в последовательном исключении неизвестных. Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе(прямой ход) система приводится к ступенчатому(в частности, треугольному) виду. На втором этапе(обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы.
21. Основное соотношение между величинами направленных отрезков на числовой оси. Координаты на прямой, плоскости и в пространстве. Формула для вычисления величины направленного отрезка на прямой через координаты его начала и конца.
22. Полярные координаты на плоскости и их связь с декартовыми прямоугольными координатами.
Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом.
Связь между декартовыми и полярными координатами
Пару полярных
координат 
и 
можно
перевести в Декартовы
координаты 
и 
путём
применения тригонометрических
функций синуса и косинуса:
в то время как две декартовы координаты и могут быть переведены в полярную координату :
(по теореме
Пифагора).
Для определения угловой координаты следует принять во внимание два следующие соображения:
Для
,
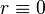может
быть произвольным действительным
числом.Для
,
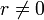чтобы получить уникальное значение
,
следует ограничиться интервалом в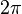 
.
Обычно выбирают интервал 
или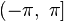 
.
Для вычисления
в
интервале
,
можно воспользоваться такими уравнениями
(
обозначает
обратную функцию к тангенсу):
Для вычисления в интервале , можно воспользоваться такими уравнениями:
Учитывая, что для вычисления полярного угла не достаточно знать отношение к , а ещё нужны знаки одного из этих чисел, многие из современных языков программирования имеют среди своих функций помимо функции atan, определяющей арктангенс числа, ещё и дополнительную функцию atan2, которая имеет отдельные аргументы для числителя и знаменателя. В языках программирования, поддерживающих необязательные аргументы (например, в Common Lisp), функция atan может получать значение координаты .