9.Показатели надежности невосстанавливаемых объектов. Средняя наработка

Показатель надежности - количественная характеристика одного или нескольких свойств надежности. Формы показателей: вероятностный, статистический.

t-время работы до отказа,

случайная величина .

Показатели надежности невосстанавливаемых объектов:

1. Функция распределения , функция надежности , плотность распределения вероятности ;

2. Вероятность отказа , вероятность безотказной работы ;

3. Интенсивность отказа ;

4. Средняя наработка до отказа .

Средняя наработка до отказа – числовая характеристика 1-го порядка, математическое ожидание наработки до отказа .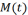

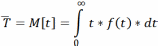
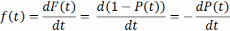
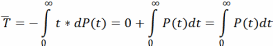
Статистическая формула для средней наработки:

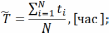
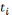– наработка до отказа показанная 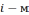устройством.

Дисперсия средней наработки – степень разбросанности показателя относительно среднего значения показателя.

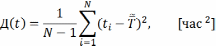
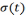- cреднее квадратическое отклонение.

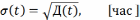
8. Показатели надежности невосстанавливаемых объектов. Интенсивность отказов

Показатель надежности - количественная характеристика одного или нескольких свойств надежности. Формы показателей: вероятностный, статистический.

t-время работы до отказа,

случайная величина .

Показатели надежности невосстанавливаемых объектов:

5. Функция распределения , функция надежности , плотность распределения вероятности ;

6. Вероятность отказа , вероятность безотказной работы ;

7. Интенсивность отказа ;

8. Средняя наработка до отказа .

Интенсивность отказов: -условная плотность вероятности отказа устройства в момент времени t при условии, что до этого момента отказы не возникали.

Вероятность безотказной работы на интервале:

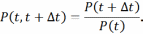
Найдем вероятность отказов на интервале :

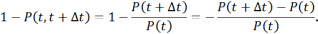
Разделим на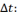

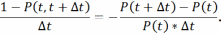
Найдем предел

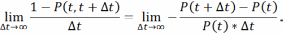
В левой части по определению – условная плотность вероятности отказов.

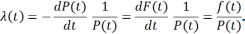
λ(t) ≥f(t)

Статистическая интенсивность отказов:

8*.

Зависимость между интенсивностью отказов и вероятностью безотказной работы:

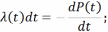
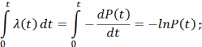
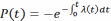
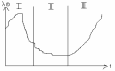
Зависимость интенсивности отказов от времени жизни изделия

только для техн. аппаратных ср-в

I-период приработки – это период от момента сбора устр-ва до начала эксплуатации. Проявляются внезапные отказы, связанные с дефектами элементной базы, монтажа.

II-период нормальной эксплуатации λ(t)=λ=const

В начальный период отказы внезапны, к концу периода появляются постепенные отказы.

III- период старения – постепенные отказы, связанные с изменением характеристик элементов.

10. Законы распределения наработки до отказа невосстанавливаемых объектов (ступенчатый, дискретный).

Закон распределения – это правило, по которому можно установить значение случайной величины. Закон распределения случ. вел. устанавливается по статистическим данным полученным в процессе испытаний, на основе процессов вызывающих отказы. Дискретная вел. может быть задана таблицей вероятности. Если случ. величина непрерывна, то ее задают ф-ей плотности распределения. Если время работы до отказа вел. дискретная, то она может быть описана законами: 1) ступенчатое распределение

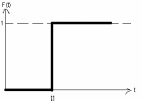
F(t)= 0, 0<t<t₁

1, t≥t₁

Вид означает, что ресурс устройства истощается мгновенно. Характерно для объектов состоящих из однотипных элементов.

2) дискретное распределение

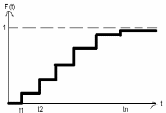
0, 0<t<t₁

F(t)= ∑от n до i=1 F_i(t), t_i≤t<n

1, t≥t_n