2.4 Обработка опытных данных

Любому специалисту в своей практической и теоретической деятельности приходится изучать зависимости между различными параметрами исследуемых объектов, процессов или систем. Изо всех способов задания зависимости между различными величинами наиболее удобным является аналитический способ (т.е. задание в виде явных функций), но в практической деятельности специалист очень часто получает зависимости между интересующими его данными экспериментально в виде таблицы. В результате возникают различные задачи по обработке опытных данных.

Интерполирование функции

Пусть дана табличная функция: y_i = f(x_i), (i = 0, n), т.е. таблица, в которой для некоторых дискретных значений аргумента x_i, расположенных в порядке возрастания, заданы соответствующие значения функции (Таблица 2.2).

Таблица 2.2 Форма табличной функции

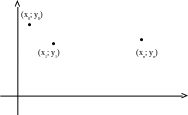
i	x	y
0	x0	y0
1	x1	y1
2	x2	y2
:	:	:
n	xn	yn

Фиг. 2.5 Расположение узловых точек на графике.

Точки с координатами (x_i, y_i) называются узловыми точками или узлами. Количество узловых точек N = n + 1. На Фиг. 2.5 табличная функция представляет собой совокупность узлов.

Задача интерполирования табличной функции (интерполяция) состоит в том, чтобы найти ее значение для любой промежуточной точки x_k  [x₀; x_n]. Задача экстраполирования функции (экстраполяция) состоит в том, чтобы найти значение функции для аргумента, лежащего вне отрезка [x₀; x_n]. Эта задача называется задачей прогноза. Обе эти задачи решаются с помощью определения некоторой аналитической функции P(x), которая приближала бы заданную табличную функцию, а в узловых точках x_i принимала бы значения y_i. Обычно искомая функция P(x) выбирается из класса алгебраических многочленов. Степень многочлена n зависит от числа узловых точек и равна n = N – 1, а интерполяционный многочлен имеет общий вид:

. (2.25)

Линейная интерполяция (y = ax + b) выполняется всего по 2-м точкам (x_i, y_i) и (x_{i + 1}, y_{i +1}) и очевидно получаем систему 2-х линейных уравнений:

(2.26)

с неизвестными a и b. Откуда:

Квадратичная интерполяция (y = ax² + bx + c) выполняется по 3-м точкам (x_i, y_i), (x_{i + 1}, y_{i +1}) и (x_{i + 2}, y_{i +2}) и получается система 3-х линейных уравнений:

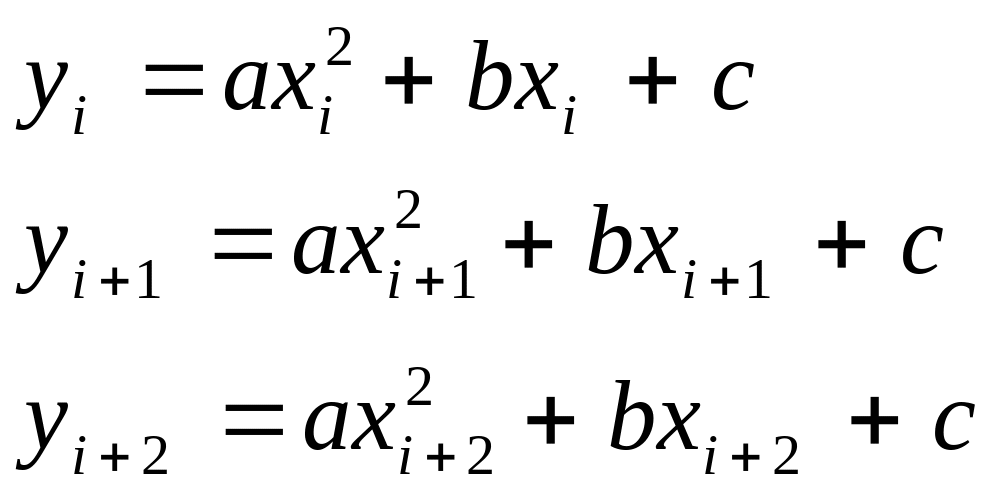(2.27)

Решая эту систему, например методом Гаусса, находим неизвестные коэффициенты a, b, c.

Аппроксимация опытных данных

Пусть мы провели некоторый эксперимент (определение длины тормозного пути автомобиля – L_т в зависимости от скорости W) в результате которого получена табличная функция, представленная на Фиг. 2.6. совокупностью узловых точек.

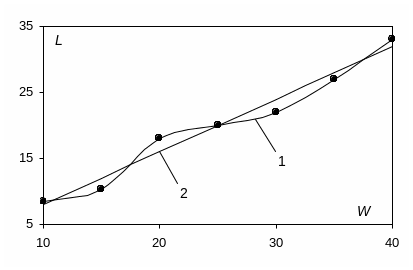
Фиг. 2.6 Длина тормозного пути автомобиля L в зависимости от скорости W.

1 – интерполяция по экспериментальным точкам; 2 – линейная аппроксимация

Для этих опытных данных необходимо решить задачу аппроксимации какой-либо аналитической зависимостью. Сущность аппроксимации опытных данных состоит в нахождении аналитического выражения некоторой функции F(x) (аппроксимирующей кривой), которая приближала бы полученную табличную функцию. Если мы попытаемся применить интерполяционный полином, то получим линию типа 1. Но эта линия не отражает суть явлений, которые мы моделируем.

Дело в том, что в эксперименте разброс результатов неизбежен и наблюдаемая величина на самом деле зависит не только от того аргумента, который у нас в таблице, а ещё и от многих других случайных факторов (изменения температуры окружающей среды, погрешностей измерительных приборов, квалификации и самочувствия работников и т.д.). Многие из этих факторов меняются по своим собственным случайным законам, которые никак не связаны с интересующей нас функцией. Все это обуславливает случайную осцилляцию табличной функции. В результате аппроксимировать опытные данные с помощью интерполяционного многочлена (особенно для высоких степеней) не целесообразно.

Метод наименьших квадратов

На практике чаще всего применяется другой метод аппроксимации опытных данных – метод наименьших квадратов (МНК). Сущность метода состоит в том, что опытные данные аппроксимируют кривой F(x), которая необязательно должна проходить через все узлы, а должна сгладить все случайные помехи табличной функции. При этом аппроксимирующую кривую F(x) стремятся провести так, чтобы все ее отклонения от табличной функции были минимальными (Фиг.2.7). Обозначим эти отклонения в виде: ₀ = F(x₀) - y₀; ₁ = F(x₁) - y₁; … _i = F(x_i) - y_i. Тогда для табличных данных, полученных в результате эксперимента, следует отыскать аналитическую зависимость кривой F(x), сумма квадратов отклонений которой по всем узлам была бы минимальной:

(2.28)

При этом аппроксимирующий многочлен (P_m) будем представлять в виде

(2.29)

Фиг. 2.7 Аппроксимация экспериментальных данных методом наименьших квадратов.

Этот аппроксимирующий многочлен не проходит через все узлы, поэтому степень многочлена не зависит от количества узлов. Как правило, степень аппроксимирующего многочлена задается, при этом всегда m < n.

Если m=1, то задача называется "линейная регрессия".

Если m=2, то задача называется "квадратичная аппроксимация".

Если m=3, то задача называется "кубическая аппроксимация".

Перепишем соотношение (2.28) в виде:

(2.30)

Необходимым условием существования минимума функции S является равенство нулю ее частных производных:

(2.31)

Дифференцируя S по каждой переменной, получаем систему линейных уравнений:

(2.32)

Порядок системы равен m + 1.

k = (0, 2m) (2.33)

j = (0, m) (2.34)

a_j (j = 0, m) – коэффициенты аппроксимирующего многочлена (неизвестные).

Решая полученную систему (например, методом Гаусса), определяем значения коэффициентов аппроксимирующего многочлена степени m. После этого следует:

• найти отклонение в каждой точке ;

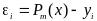• определить сумму квадратов отклонений по всем узлам ;

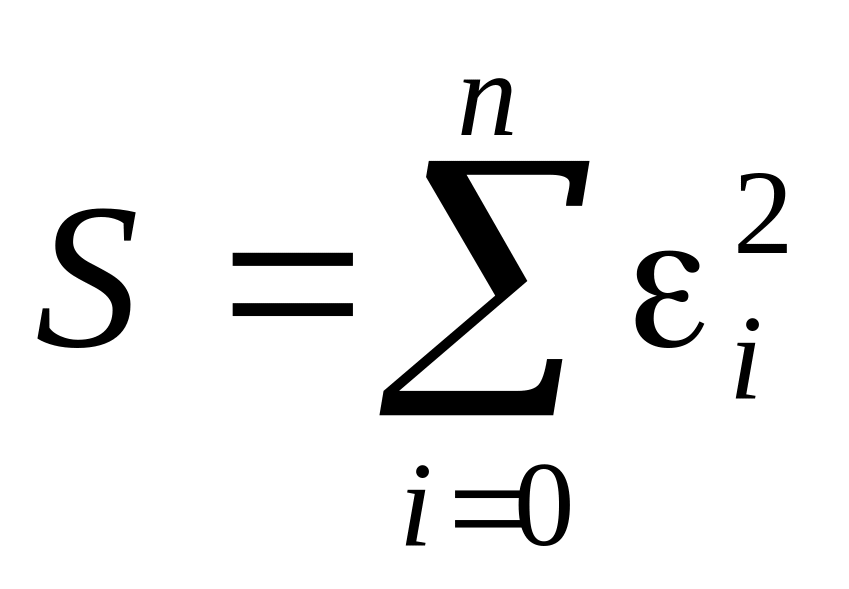• вычислить остаточную дисперсию по формуле:

. (2.35)

Контрольные вопросы.

1. Приведите пример постановки задачи для создания математической модели:

а) охлаждения двигателя легкового автомобиля;

б) износа дорожного покрытия (асфальта);

в) обтекания грузового автомобиля;

г) оптимизации расписания занятий в институте.

2. Какая разница между параметрами и характеристиками математической модели?

3. Почему постановка задачи является важным этапом математического моделирования?

4. Для чего необходимы допущения в физической схеме? В чем их смысл?

5. Проанализируйте допущения и базовые уравнения задачи о нейтрализаторе. Дайте варианты ответов:

а) если убрать допущение о превращении NO только в каталитическом слое, то какие уравнения необходимо скорректировать и надо ли вводить новые уравнения?

б) если убрать допущение о пренебрежимости падения давления вне каталитического слоя, то какие уравнения необходимо скорректировать?

в) если убрать допущение о равенстве температур продуктов сгорания и каталитического слоя, то какие уравнения необходимо скорректировать и надо ли вводить новые уравнения?

6. Проанализируйте допущения и базовые уравнения задачи об охлаждении мастерской. Дайте варианты ответов:

а) какие уравнения должны измениться, если отбросить допущение о равенстве температуры воздуха и оборудования?

б) если стены мастерской сконструированы из 2-х различных материалов (например, дерево и бетон), то какие уравнения должны измениться?

в) какие уравнения должны измениться, если учитывать, что тепло уходит через пол и потолок?

7. Охарактеризуйте величины и зависимости типа “черный ящик”.

8. Какие величины имеют свойства “черного ящика”:

- в задаче о нейтрализаторе;

- в задаче об охлаждении мастерской;

- в задаче о соотношении зарплаты и числа работающих.

9. Найти размерности величин, фигурируемых в уравнениях (2.8, 2.9).

10. Привести в систему СИ следующие величины:

- коэффициент теплоотдачи ;

- коэффициент динамической вязкости ;

- константа скорости химической реакции .

11. Перевести из системы СИ:

- коэффициент теплопроводности в единицы ;

- теплоемкость в единицы ;

- коэффициент динамической вязкости в единицы .

12. Мощность автомобиля W_a = 70 л.с., мощность ТЭЦ W_т = 80000квт. Определить во сколько раз мощность ТЭЦ больше W_a?

13. Дано уравнение:

(К1)

где [Q] = дж/сек; λ – коэффициент теплопроводности; F – площадь стенки; T – температура; [x] – м. Проверяя размерность показать, что уравнение (К1) неверно. Дать вариант правильного уравнения.

14. В уравнении состояния Ван дер Ваальса найти размерности величин a, b, R. Учесть, что н∙м = дж; p – давление; [v] = м³/кг; T – температура.

15.Какая разница между интерполяцией и экстраполяцией?

16. Какая разница между интерполяцией и аппроксимацией?

17.Дана таблица результатов экспериментов (энтальпия вещества в зависимости от температуры).

N˚ точек	т0	т1	т2	т3	т4	т5
T(K)	300	600	900	1200	1500	1800
H(кдж/кг)	2,1	272,1	542,4	809,3	1080	1349

Необходимо выполнить:

а) линейные интерполяции энтальпии между точками т₀ и т₅ а также между точками т₂ и т₃.Определить средние теплоемкости для каждого интервала по формуле:

C_p = (H_j – H_i)/( T_j - T_i )

б) выполнить квадратичную интерполяцию по точкам т₀, т₃, т₅, т.е. определить коэффициенты a, b, c в зависимости : H = aT² + bT + c

18.Изложите идею метода наименьших квадратов. Почему в нем используется не отклонение ε, а квадрат отклонения ε² ?

19.Дана экспериментальная зависимость изменения зарплаты p(t) с возрастом.

Возраст(лет)	20	24	28	32	36	40
Зарплата(тыс.руб)	4,5	6,9	9,4	11,6	13,1	15,1

Выполнить линейную аппроксимацию (m = 1) по МНК, т.е. найти коэффициенты аппроксимации и дисперсию.