2.3 Соотношения между единицами измерения

Несмотря на наличие международной системы СИ в разных странах и разных сферах деятельности используются различные “региональные” системы единиц измерения. Например, в англо-язычных странах используется собственная система единиц. Ниже показана связь этой системы с системой СИ:

1 фут (ft) = 0,305 м; 1 дюйм (in) = 25,4 мм; 1миля (сухопутная) = 1609 м;

1 ярд (jd) = 0,914 м; 1 фунт (pd) = 0,3454 кг.

Кроме того, до сих пор используются внесистемные единицы, например:

а) T(F) = t(C) + 32; t(C) = T(K) – 273 (2.10)

где T(F) – температура по Фаренгейту; t(C) - температура по Цельсию, отсюда можно получить, что 1˚F = 5/9˚C = 5/9˚K.

б) 1 калория = 0,001 Ккал = 4,184 дж; 1 л.с. = 75 кГм/сек (2.11)

1 кГм = 9,81 дж; 1кГ = 9,81 ньютон (н) и т.д. (2.12)

На этапе создания физической схемы или математической модели часто используется справочная информация во внесистемных или региональных единицах. Поэтому необходимо уметь переводить величины из одной системы в другую, принятую в создаваемой математической модели, иначе можно допустить грубую ошибку. Этот перевод не является сложным, но его надо проводить аккуратно. Ниже мы даем простую технику этого перевода и соответствующие примеры:

а) допустим требуется перевести давление, заданное в технических атмосферах (P = 15 кГ/см²) в Паскали (Pa = н/м²). Зная, что 1кГ = 9,81 н и 1м = 100 см проведем замену “кГ” на “9,81 н” и “см” на “0,01м”, тогда получим:

(2.13)

б) перевести мощность двигателя, выраженную в лошадиных силах, W = 60л.с. в киловатты (1квт = 1000ватт), учитывая (2.11, 2.12):

(2.14)

в) перевести коэффициент теплопроводности, выраженный во внесистемных единицах , в единицы системы СИ, учитывая (2.10, 2.11) и что 1 час = 3600 сек. Заменяя соответствующие единицы, легко получим:

(2.15)

г) перевести плотность железа в единицы системы СИ. Учитывая, что 1г = 0,001кг, получим:

(2.16)

д) можно также проводить “обратные” преобразования из системы СИ во внесистемные единицы. Так в химии часто используется универсальная газовая постоянная . Получим это значение зная, что и учитывая (2.11):

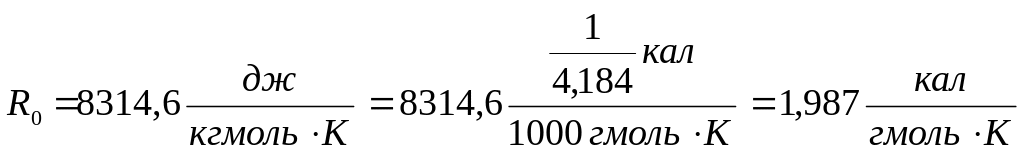(2.17)

что и требовалось определить.

В физических (концептуальных) схемах и математических моделях используются соотношения, где символы в основном обозначают какую-либо размерную величину. Эту особенность можно использовать для контроля за правильностью математических преобразований. Имеется ряд свойств, которые позволяют на основе учета размерностей локализовать некоторые ошибки при выводе уравнений. Среди этих свойств можно указать следующие:

1) Слагаемые в уравнениях должны иметь одинаковые размерности. Например, в уравнении Бернулли:

(2.18)

- для первого слагаемого имеем: , где [ ] – означает операцию извлечения размерности;

- для второго слагаемого имеем: ;

- для третьего слагаемого имеем: ,

т.е. все 3 слагаемые имеют одинаковые размерности и если в каком-либо полученном вами уравнении окажутся слагаемые с разными размерностями, то это означает, что где-то при выводе (или при “списывании”), была допущена ошибка.

2) В дифференциальных уравнениях символы d,  считаются не имеющими размерности, т.е. . Например, из уравнения:

(2.19)

имеем: ; ;

где размерности: энтропии ; удельной энтальпии ; удельного объема .

3) В дифференциальных операторах символы также не имеют размерности, а операторы типа имеют размерности . Например, из уравнения:

(2.20)

имеем: .

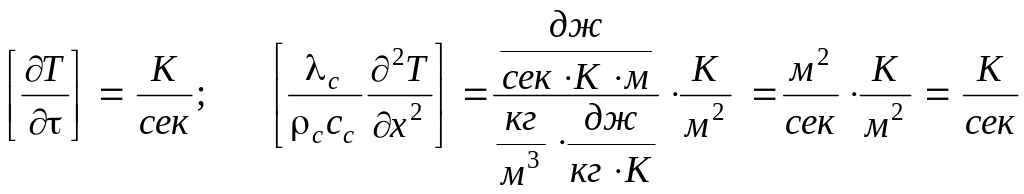4) Если в формулах или уравнениях фигурируют операции типа: sin(x), log(x), exp(x) и т.д., то аргументы x должны быть безразмерными (угловые градусы и радианы считаются безразмерными величинами). Примеры:

- уравнение гармонических колебаний:

(2.21)

где [] = 1/сек; [] = сек, т.е. [] – безразмерная величина;

- формула для константы скорости поверхностной реакции:

(2.22)

где размерность энергии активации [E] = кал/гмоль; . Тогда - безразмерная величина. Логарифмируя (2.22) получим:

(2.23)

Так как k и A имеют размерности [k] = [A] = 1/сек, то кажется, что относительно логарифма правило безразмерности аргумента нарушается, но однако в уравнениях математических моделей (базирующихся на физических законах) в формулах типа (2.23) всегда встречается разность логарифмов, которая обеспечивает безразмерность логарифма. Действительно из (2.23) имеем: , откуда следует, что x = k/A - безразмерная величина.

5) В физических схемах и математических моделях часто встречаются интегралы, размерность которых определяются по формуле: . Например:

(2.24)

Проверим размерности обеих частей соотношения (2.24), считая [x] = [S] = м; .

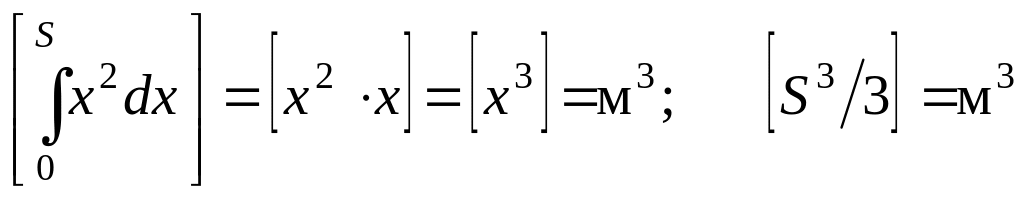Рассмотрим интеграл и его явное выражение: . Кажется, что размеры правой и левой частей – различны. Но учитывая, что аргументы тригонометрических функций должны быть безразмерные величины, приходим к выводу, что в этом выражении нарушение по размерности отсутствует.