26

Тема 2. Постановка задачи и создание физической (концептуальной) схемы

2.1 Постановка задачи: примеры и варианты.

Этап постановки задачи, несмотря на кажущуюся простоту, является очень важным, весьма сложным этапом, требующим интуиции и опыта. Если задача поставлена неправильно, то в последующем это приводит к потере времени и средств и к досадному чувству зря выполненной работы. Постановка задачи, как правило, связана с некоторым риском, требует глубокого осмысления, прогнозирования времени и средств, необходимых на создание модели. Очень важным на этом этапе является поиск и изучение уже решенных задач (прототипов), близких к создаваемой модели. Конечно же, существуют достаточно простые “стандартизированные” постановки задач, например, задание на курсовой проект или на типовой дипломный проект.

Но значительно чаще предлагаются сложные задачи: оптимальный раскрой материала, рациональный выбор автобусных междугородных маршрутов, уменьшение токсичности выхлопных газов из двигателя, моделирование работы сушильных агрегатов, очистка сточных вод, модель автоматического управления химическим реактором и т.д.

Постановка задачи – это не есть высказанное желание что-то сделать (например, если директор агропредприятия сказал, что надо увеличить производительность сушилки зерна с применением методологии математического моделирования это не означает, что он поставил задачу создания математической модели сушки зерна). При постановке задачи необходимо, по крайней мере, составить перечень характеристик, которые должны вычисляться по планируемой математической модели и сформировать набор параметров, от которых должны зависеть эти характеристики. Рассмотрим некоторые примеры постановки задач в различных областях знаний.

A. Нейтрализатор NO_x продуктов сгорания автомобильного двигателя.

В постановке задачи должна быть задана принципиальная схема нейтрализатора (Рис. 2.1).

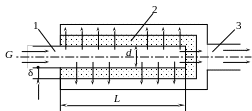
Фиг. 2.1 Схема нейтрализатора продуктов сгорания.

1 –вход продуктов сгорания; 2 – блок катализатора; 3 – выход очищенных продуктов сгорания.

В блоке катализатора находится вещество (катализатор), которое инициирует протекание реакций типа: NO + NO  N₂ + O₂ при низких температурах. Известно, что чем больше толщина этого блока, тем полнее протекает реакция и тем меньше концентрация NO_x на выходе из нейтрализатора. Однако, чем больше величина  и расход G, тем больше потери давления (P_н) в нейтрализаторе. Кроме схемы нейтрализатора заданы также: тип катализатора; состав, расход (G) и температура продуктов сгорания на входе (T_в); толщина каталитического слоя () и его диаметр (d) и длина (L). Оговариваются также финансовые ресурсы и время, необходимое для разработки модели. Необходимо определить следующие характеристики: концентрация NO_x на выходе из нейтрализатора ( ) и потери давления в нейтрализаторе (P) в зависимости от параметров G, , d, , L, T_в.

B. Охлаждение помещения мастерской по ремонту автомобилей.

Пусть имеется некоторая мастерская с оборудованием, работающая в зимних условиях (Рис. 2.2). Помещение обогревается батареями центрального отопления, с нормальной температурой внутри (например, T_п = 20С) и низкой температурой снаружи (T_а = - 20С).

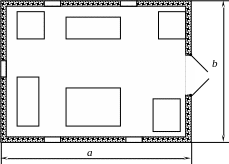
Фиг. 2.2 Схема мастерской для ремонта автомобилей

Известны геометрические размеры всего помещения, масса, находящегося в нем оборудования, и теплофизические свойства материалов внешних стен. Допустим, что внезапно прекращается подача тепла. Тогда необходимо определить за какое время температура в помещении понизится до критической (Т_кр = 0С). В этой задаче параметрами являются: геометрия помещения, масса имеющегося оборудования, теплофизические свойства материалов стен, температуры (Т_кр, Т_а), а характеристика, которую надо определить, является зависимость изменения Т_п по времени.

C. Изменение зарплаты и занятости.

Рынок труда, на котором взаимодействуют работодатели и наемные рабочие, характеризуется зарплатой р(t) и числом занятых N(t). Пусть на нем существует равновесие, т. е. ситуация, когда за плату р_u > 0 согласны работать N_u > 0 человек. Если по каким-то причинам это равновесие нарушается (например, когда часть работников уходит по возрасту на пенсию либо у предпринимателей возникают финансовые трудности), то функции р(t) и N(t) отклоняются от значений р_u, N_u. Необходимо описать изменения величин р(t) и N(t) при внезапном отклонении одной из этих характеристик от равновесия (например, p₀ < p_u). Как правило, совокупность параметров в таких задачах будет полностью определена лишь после набора статистических данных или выполнения углубленного обзора по прототипам.

D. Рационализация питания учащихся техникума.

Пусть в некотором учебном заведении учащиеся обедают за счет средств муниципалитета. На эти средства приобретаются разнообразные продукты: хлеб, мясо, масло, овощи, крупы и т.д. Набор этих продуктов задан. При этом допускается варьирование количества закупаемых продуктов, например, можно больше купить масла и меньше овощей, больше круп и меньше хлеба и т.д. Цены на 1 кг каждого продукта известны, известно также количество полезных веществ (белков, жиров, углеводов и витаминов) в каждом типе продукта. Заданы также (согласно медицинским нормам) среднее количество полезных веществ, требуемых для каждого учащегося в течение недели (см Таблицу 2.1). Число учащихся является известным. Необходимо найти наиболее рациональное (в финансовом смысле) распределение между закупаемыми продуктами.

Таблица 2.1 Распределение полезных веществ в продуктах, цены на продукты и количество полезных веществ в неделю, необходимое на одного учащегося.

	Мясо	Крупа	Масло	Овощи	Хлеб	Кол-во*
Белки	0,7	0,2	0,01	0,05	0,1	≥ 0,9
Жиры	0,15	0,05	0,7	0,05	0,05	≥ 0,3
Углеводы	0,1	0,7	0,01	0,7	0,75	≥ 1,8
Витамины	0,05	0,05	0,1	0,2	0,1	≥ 0,3
Цена (руб/кг)	180	20	100	40	15

* - количество полезных веществ в неделю, необходимое на одного учащегося

Параметрами задачи будут величины, приведенные в Таблице 2.1, а характеристиками (т.е. искомыми величинами) – количество мяса, масла, крупы, овощей и хлеба, которые надо закупить на 1 неделю, а также суммарные затраты за этот период.

E. Система вентиляции в ремонтной мастерской.

Допустим, что необходимо разработать математическую модель вентиляционной системы мастерской по ремонту автомобилей. В принципе в этой модели требуется по заданному расходу воздуха и заданной схеме трубопроводов определить площади и длины трубопроводов, места расположения и площади выходных каналов (Рис. 2.3).

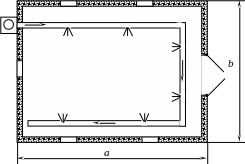
Фиг. 2.3 Схема системы вентиляции в мастерской

Расположение выходных каналов должно обеспечивать эффективную продувку помещения. Чем больше площадь трубопроводов, тем меньше потери давления на различных участках и тем менее мощный требуется вентилятор. В зависимости от условий, в которых разрабатывается математическая модель (располагаемых резервов времени и финансовых ресурсов), а также от желания заказчика можно сформировать (в качестве примера) несколько вариантов этой задачи.

е1) “Учебный” вариант - дипломный проект (времени на создание модели мало, финансовые ресурсы отсутствуют). Заданы средние скорости W_i на каждом участке и на выходах, места расположения выходных каналов и общий расход воздуха. Характеристики вентилятора определять не требуется. Надо определить длины и площади трубопроводов, потери давления на каждом участке P_i и суммарные потери P_.

е2) “Производственный” вариант (время на создание математической модели значительно больше, чем в варианте е1, имеются небольшие финансовые ресурсы на разработку модели). Задается геометрия помещения и общий расход (G). Надо определить W_i, P_i, P_, длины и площади трубопроводов, а также число и места расположения выходных каналов и характеристики вентилятора.

е3) “Научный” вариант (время и финансовые ресурсы на создание модели еще больше, чем в варианте е2). Задаются размеры помещения, расположение оборудования, расход G. Необходимо определить: W_i, P_i, P_, длины и площади трубопроводов, места расположения выходных каналов, а самое главное, поле течения воздуха в помещении с целью исключения застойных зон.