3.1.9. Проводники в электрическом поле

3.1.9.1. Распределение избыточного заряда на проводниках в состоянии равновесия

К проводникам относятся вещества, проводящие электрический ток. В них имеются свободные заряды, которые способны перемещаться по проводнику под действием внешнего электрического поля. В металлических проводниках свободными зарядами являются электроны, они образуют газ, заполняющий кристаллическую решетку положительно заряженных ионов.

Рассмотрим, что произойдет, если проводнику сообщить избыточный заряд. При этом положительному заряду металлического проводника соответствует недостаток свободных электронов, а отрицательному заряду – их избыток. В условиях равновесия избыточного заряда справедливы следующие утверждения:

1.Электрическое поле внутри проводника отсутствует, а объем проводника и его поверхность являются эквипотенциальными

(3.41)

Действительно, если равенства (2.39) не выполняются, то тогда свободные заряды в проводнике будут перемещаться, так как работа сил электрического поля не будет равна нулю ( ). Это противоречит условию равновесия избыточного заряда: в условиях равновесия они должны быть неподвижными.

2.Избыточный заряд распределяется только по внешней поверхности проводника, так как из-за кулоновского отталкивания одноименных зарядов они стараются разойтись на максимально возможные расстояния друг от друга.

Это утверждение можно доказать, используя теорему Гаусса. Выберем внутри проводника произвольную замкнутую поверхность (рис.3.14,а) и рассчитаем поток вектора через нее в условиях равновесия. Учтем, что связанных зарядов в металле не возникает (q' =0) и поэтому из формулы (3.27) следует

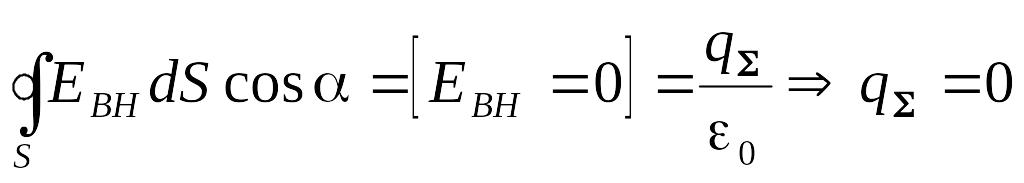
т.е. внутри такой поверхности избыточного заряда нет, так как этот заряд одного знака. Следовательно, он располагается только на внешней поверхности проводника.

3.Распределение избыточного заряда по внешней поверхности проводника является неравномерным: модуль вектора и поверхностная плотность заряда σ больше в тех точках поверхности проводника, где ее кривизна больше.

Кривизну поверхности в какой-либо ее точке можно определить радиусом R вписанной вблизи этой точки сферы, а именно, кривизна поверхности обратно пропорциональна R.

Докажем третье утверждение. Для этого отметим, что выводы об электрическом поле равномерно заряженной по поверхности сферы, сделанные в параграфе 3.1.8, справедливы и в случае заряженной металлической сферы или шара, так как кривизна поверхности во всех ее точках одинакова, т.е. избыточный заряд распределяется по ней равномерно.

Если учесть, что поверхность проводника можно представить в виде совокупности разных участков вписанных в нее сфер (рис.3.14,б) и использовать формулы (3.39) для Е и φ на поверхности сферы, то тогда можно записать:

(3.42а)

(3.42б)

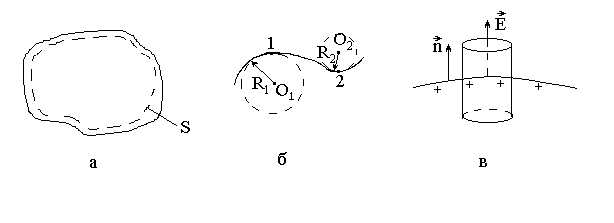
Рис.3.14

Согласно формуле (3.42б) модуль вектора вблизи какой-либо точки поверхности заряженного проводника пропорционален поверхностной плотности заряда σ в этой точке. Формулу (3.42б) можно было получить на основе теоремы Гаусса, выбирая вспомогательную замкнутую поверхность в виде цилиндра малого объема, образующая которого перпендикулярна к поверхности проводника (рис.3.14,в). Считая в пределах цилиндра электрическое поле однородным и применяя формулу (3.29) придем к выражению (3.42 б).

На рис. 3.15,а приведено графическое изображение с помощью линий электрического поля заряженного проводника сложной формы.

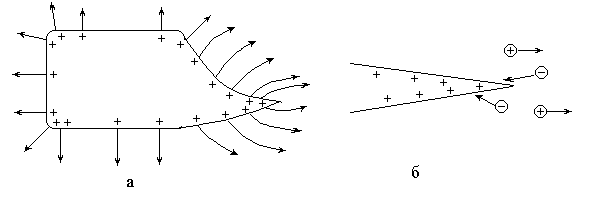
Рис.3.15

Нужно учесть, что линии во всех точках перпендикулярны к поверхности металла, так как она является эквипотенциальной поверхностью.

Вблизи острия модуль вектора может превысить значение, соответствующее ионизации молекул воздуха (Е_иониз≈310⁶ В/м при атмосферном давлении), и тогда возникает явление стекания зарядов, сопровождающееся электрическим ветром.

Образующиеся при ионизации молекул электроны движутся к острию и компенсируют на нем часть заряда, равновесие зарядов на проводнике нарушается и к острию подходят заряды с других участков поверхности проводника (рис.3.15,б). Это движение продолжается до тех пор, пока модуль напряженности электрического поля вблизи острия будет превышать Е_иониз. В

то же время положительные ионы молекул воздуха движутся в противоположном направлении, от острия, увлекают за собой нейтральные молекулы, создавая движения воздуха - электрический ветер.

Тот факт, что избыточные заряды в состоянии равновесия находятся только на внешней поверхности проводника, позволяет создать устройства, способные накапливать большие заряды и достигать разности потенциалов в несколько миллионов вольт. К ним можно отнести электростатический генератор Ван-де-Граафа.

Рис.3.16

Он представляет собой металлическую сферу 1, закрепленную на изолирующей колонне 2 (рис. 3.16). На металлическую щетку 3 поступаетположительный заряд от источника напряжения 4 в несколько десятков киловольт. Вблизи остриев щетки напряженность электрического поля превышает Еиониз молекул воздуха (радиус острия щетки r~1 мм, Е = 107 В/м) и заряд стекает на диэлектрический транспортер 5 – движущуюся замкнутую ленту из прорезиненной ткани. Эта лента подает заряд внутрь металлической сферы, он стекает на щетку и сразу поступает на внешнюю поверхность сферы. Максимально достижимая разность потенциалов Uмакс в таком устройстве ограничивается явлением стекания заряда с поверхности сферы, т.е. возникновением разряда в воздухе при Есф≥Еиониз. Величина Uмакс составляет порядка 10 мегавольт при радиусе сферы R=5 м

Электрические генераторы подобного типа используются главным образом в высоковольтных ускорителях заряженных частиц, а также в слаботочной высоковольтной технике.