3.1.4. Принцип суперпозиции электростатических полей. Примеры расчета вектора напряженности и потенциала для некоторых частных случаев распределения зарядов
Для
расчета
и
поля, созданного системой зарядов или
макроскопическим заряженным телом,
используют принцип суперпозиции, а
именно: вектор напряженности
(потенциал
)
электрического поля, созданного
несколькими зарядами, равен векторной
сумме напряженностей (алгебраической
сумме потенциалов) полей, созданных
каждым зарядом в отдельности (
)
(3.11)
В
случае макроскопического заряженного
тела для оценки
и
в какой- либо точке A (рис.3.3 а) разбивают
тело на малые объемы, которые можно
рассматривать как точечные заряды
;
находят по формулам (3.9) и (3.10) вектора
и потенциалы
от этих зарядов в т. А и затем суммируют
все
и
,
т.е. берут интеграл по объему V тела
Рис.3.3
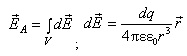(3.12)
(3.13)
Принцип
суперпозиции позволяет также рассчитывать
потенциальную энергию взаимодействия
зарядов. Так, для системы точечных
зарядов
(
)
можно записать
,
(3.14)
где
-
потенциал поля, созданного всеми
зарядами, кроме i – го заряда, в месте
расположения i – го заряда; коэффициент
(1/2) входит в формулу из-за того, что
взаимодействие двух зарядов в сумме
учитывается дважды.
Рассмотрим ряд конкретных примеров расчета электростатических полей по формулам (3.12) и (3.13).
1.
Поле диполя. Под электрическим диполем
понимают электронейтральную систему
близкорасположенных двух точечных
зарядов, отстоящих друг от друга на
расстояние l (рис.3.3,б).
Для описания электрического поля,
созданного диполем, вводят понятие
дипольного момента
:
это вектор, направленный по прямой от
заряда (+q) к заряду
(-q), т.е. по оси
диполя, и равный по модулю произведению
модуля одного из зарядов на расстояние
l между ними
(3.15)
Обычно при описании поля диполя рассматривают точки, находящиеся на расстоянии r значительно превышающие расстояние l между зарядами диполя (r >> l).
Рассчитаем
модуль вектора
и потенциал φ в точках А, В, С, отстоящих
от центра диполя (точка О) на расстоянии
r; линии ОА, ОВ и ОС составляют с осью
диполя углы 0,
и произвольный угол
(рис.3.4).
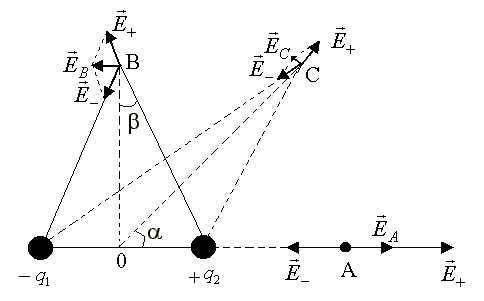
Рис.3.4
Используя
принцип суперпозиции (3.9), (3.10), найдем
направление и модули векторов
,
а также потенциалы
в этих точках.
Точка А: = 0.
;
.
Точка В: =90.
,
=
;
.
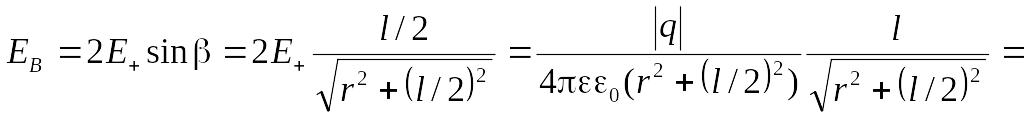
Для точки С, расположенной под произвольным углом , можно получить общее выражение, включающее в себя частные случаи для
точек А и В:
.
(3.16)
Из
формулы (3.16) следует, что модуль вектора
напряженности
и потенциал
поля диполя на расстояниях r >> l
определяются модулем его дипольного
момента
,
причем они уменьшаются в зависимости
от расстояния r быстрее, чем для поля
точечного заряда (формулы (3.9),(3.10)).
2.
Электрическое поле на оси равномерно
заряженного кольца. Пусть равномерно
заряженное по длине кольцо радиусом R
несет заряд q. Найдем
направление и модуль вектора
,
а также потенциал
поля кольца в точке А, расположенной на
оси кольца на расстоянии l
от его центра (рис.3.5).
Рис.3.5
Для
этого разбиваем кольцо на малые участки
– точечные заряды dq, определяем
направление векторов d
от всех зарядов dq в точке А и используем
для расчета
формулу (3.12). Из симметрии задачи видно,
что все вектора d
образуют конус векторов с углом
при его вершине и суммарный вектор
будет направлен вдоль оси, вверх. Тогда
;
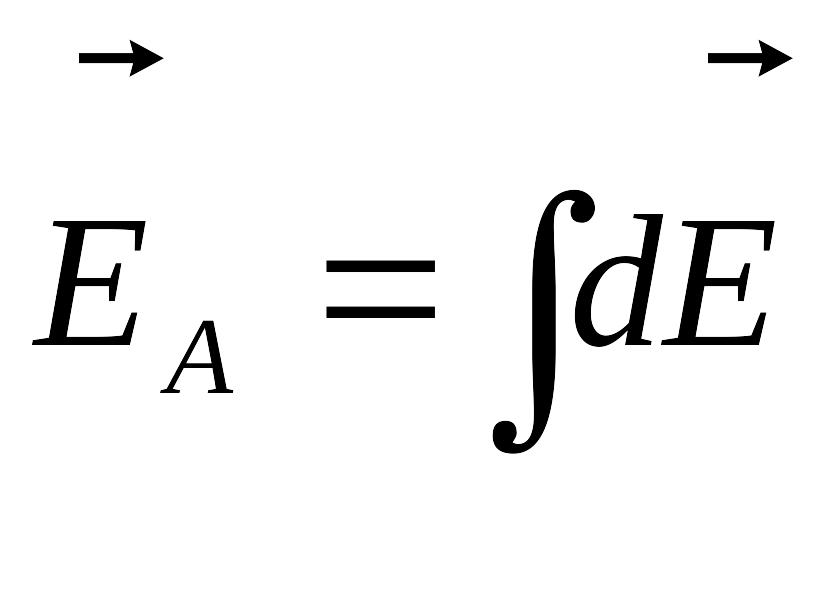Oy:
;
.
Итак,
(3.17)
Из формулы (3.17), в частности, следует, что в центре кольца, в точке О, (l=0)
(3.18)
На
расстояниях l, значительно превышающих
радиус R кольца (l >>R), его можно
рассматривать как материальную точку,
а электрическое поле кольца как поле
точечного заряда. Действительно,
пренебрегая в формулах (3.17)
по сравнению с
,
получим:
l>>R:
,
.