3.2. Постоянный электрический ток

3.2.1. Сила тока. Плотность тока

Под электрическим током понимают упорядоченное движение заряженных частиц, причем за направление тока принимают направление движения положительных зарядов.

Электрический ток существует при наличии свободных зарядов и электрического поля. Такие условия можно создать в вакууме и в различных средах, таких как твердые тела (металлы, полупроводники), жидкости (жидкие металлы, электролиты) и в газах. Обычно рассматривают протекание тока в металлических проводниках, где свободными носителями заряда являются электроны.

Протекание тока по проводнику характеризует сила тока I , определяемая по формуле

(3.70)

где - заряд, проходящий через поперечное сечение проводника за время .

Сила тока является алгебраической величиной, она может быть как больше, так и меньше нуля. Это, например, проявляется при расчетах сложных электрических цепей, где трудно указать правильное направление тока в каждой части цепи (см. параграф 3.2.4).

Для постоянного тока величина I остается одинаковой и по модулю и по направлению, что позволяет в формуле (3.69) выбирать конечные значения заряда и времени

(3.71)

Распределение тока по сечению проводника характеризует вектор плотности тока , направление, которого в каждой точке проводника совпадает с направлением тока, т.е. с направлением скорости упорядоченных положительных зарядов ( ). Модуль вектора равен

(3.72)

где - сила тока, протекающего в данной точке внутри проводника через элементарную площадку , расположенную перпендикулярно к направлению тока (рис.3.32,а).

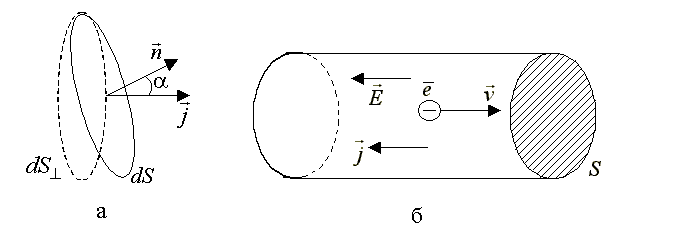
Рис.3.32

Введение вектора плотности тока позволяет найти силу тока, протекающего через любую поверхность S

(3.73)

В этой формуле угол α это угол между вектором и вектором нормали к элементарной площадке (рис.3.32,а).

Представляет интерес выразить вектор плотности тока через характеристики, описывающие движение свободных зарядов в проводнике. В качестве примера рассмотрим электрический ток в металле, где валентные электроны образуют газ свободных частиц, заполняющих кристаллическую решетку положительно заряженных ионов.

В отсутствии электрического поля электроны участвуют в тепловом движении со средней арифметической скоростью < >, составляющей при комнатной температуре величину порядка 100 км/с.

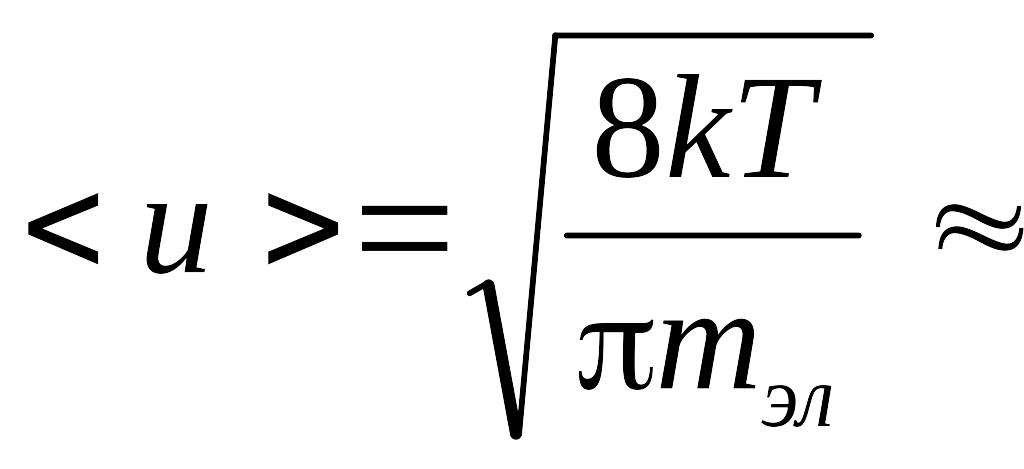1 105 м/с

Из-за хаотичности теплового движения электронов электрического тока не возникает ( =0), так как через поперечное сечение проводника в обе стороны проходит одинаковое число электронов и поэтому суммарный перенос заряда равен нулю.

При включении электрического поля у электронов появляется добавочная скорость   - скорость направленного движения под действием сил электрического поля; она по модулю примерно равна ~ 1 мм/с, что существенно меньше модуля скорости < >. Но именно скорость   обеспечивает наличие тока в проводнике. Образно говоря, при включении электрического тока в металле появляется электрический ветер, смещающий все хаотически движущиеся электроны в одном направлении.

Через поперечное сечение проводника площадью S за время t пройдут все электроны, находящиеся в цилиндре высотой (Vt) (рис.3.32,б). Если ввести характеристику металла – концентрацию n свободных электронов, то тогда можно получить:

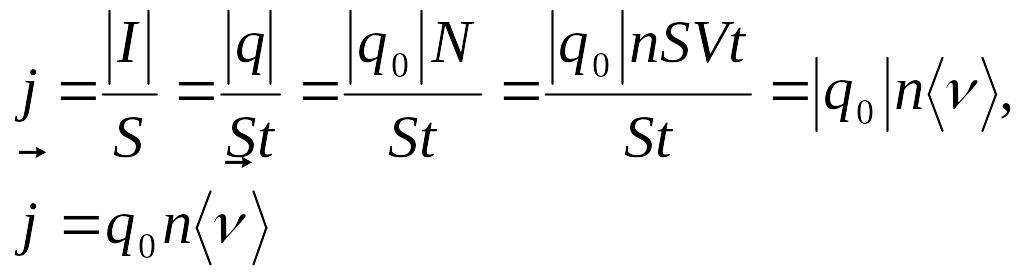(3.74)

где - это заряд электрона или, в общем случае, свободной заряженной частицы, участвующей в создании электрического тока;   - средняя скорость направленного движения заряженной частицы.

Формула (3.74) справедлива для любых модельных теорий описания электрического тока (классической или квантовой теории электронного газа), так как она была получена из общих представлений о движении заряда в проводниках. Это, несомненно, повышает ее ценность и значение.

В заключение этого параграфа приведем оценку числового значения модуля средней скорости   направленного движения свободных электронов в металле. Учитывая числовые значения концентрации свободных электронов в металле 1029 м-3 и предельно допустимую плотность тока в медном проводнике А/м2, из формулы (3.73) получим

м/с.