3.1.12.7. Пьезоэлектрики. Сегнетоэлектрики

Диэлектрики в науке и технике используются, прежде всего, как электроизоляционные материалы. Однако имеются и другие разнообразные применения диэлектриков из-за наличия у отдельных их групп необычных свойств.

Пьезоэлектрики. В этих диэлектриках наблюдается пьезоэлектрический эффект, а именно, деформация диэлектрика сопровождается его поляризацией (рис.2.30) и ,наоборот, поляризация диэлектрика приводит к его деформации.

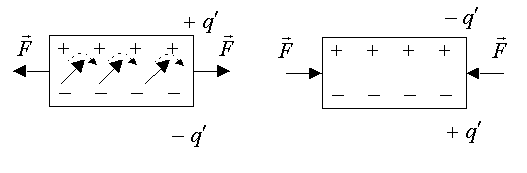
Рис. 3.28

Причем смена знака деформации (растяжение заменяется сжатием) приводит к смене знака поляризации (рис.3.28, изменяется знак поверхностных зарядов ) и наоборот. Поляризация пьезоэлектриков объясняется поворотом молекулярных диполей при их деформации (рис.3.28).

Нужно отличать пьезоэффект от явления электрострикции, который наблюдается у всех диэлектриков и состоит в изменении размеров диэлектрика под действием внешнего электрического поля. Но в случае электрострикции смена направления внешнего электрического поля не приводит к смене знака его деформации.

К пьезоэлектрикам относят, например, такие диэлектрики, как кварц, сегентовая соль, титанат бария и т.д., всего известно порядка 1500 пъезоэлектриков. Они нашли широкое применение в электроакустических приборах для преобразования механических (звуковых и ультразвуковых) колебаний в электрические и обратно, в датчиках давления и т.д.

Сегнетоэлектрики. К ним относят пьезоэлектрики, обладающие самопроизвольной (спонтанной) поляризацией в отсутствие внешнего электрического поля. Она может существенно изменяться под влиянием различных внешних факторов. Отметим ряд необычных свойств сегнетоэлектриков.

1. Относительная диэлектрическая проницаемость может достигать нескольких тысяч единиц, тогда как у обычных диэлектриков она достигает несколько сотен единиц.

2. Между молекулами устанавливается взаимодействие, которое приводит к параллельной ориентации дипольных моментов молекул в макроскопических областях, называемых доменами. Направление дипольных моментов молекул в разных доменах разное, поэтому в отсутствие электрического поля вектор поляризации сегнетоэлектрика равен нулю (рис.3.29,а).

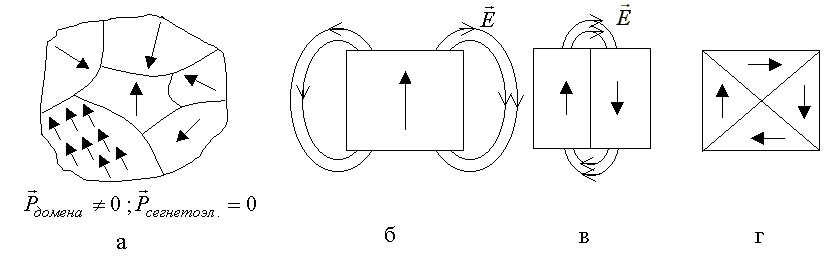
Рис.3.29

Размеры доменов устанавливаются за счет действия двух факторов:

1) энергетически выгодно увеличивать число доменов, так как уменьшается энергия для поддержания электрического поля за пределами сегнетоэлектрика (рис.3.29,б,в,г); 2) энергетически выгодно уменьшать число доменов из-за того, что уменьшается длина границ между доменами, на которых накапливается энергия электрического поля из-за резкого изменения направления дипольных моментов молекул соседних доменов.

3.Зависимость вектора поляризации от модуля напряженности электрического поля является нелинейной и в сравнительно слабых полях достигается насыщение. Это связано с тем, что вдоль поля устанавливаются сразу же все молекулы отдельных доменов.

Поляризация сегнетоэлектрика сопровождается сначала увеличением объемов доменов с выгодной ориентацией дипольных моментов молекул относительно электрического поля (для них угол между векторами и наименьший, рис.3.30 участок 0-1).

Рис.3.30

В итоге образец становится однодоменным (рис.3.30, состояние 1). Затем происходит поворот вектора ; он устанавливается вдоль вектора электрического поля (процесс вращения) и образец становится поляризованным до насыщения.

4. Для сегнетоэлектриков наблюдается явление гистерезиса –явление неоднозначной зависимости вектора поляризации от электрического поля .

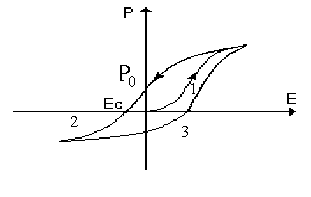
Рис. 3.31

Если после достижения состояния насыщения уменьшать модуль вектора , то изменение модуля будет отставать от изменения модуля (рис.3.31). При сегнетоэлектрик остается поляризованным, значение называется остаточной поляризованностью. Для того чтобы убрать остаточную поляризацию, необходимо приложить внешнее поле противоположного направления. Значение , при котором поляризация сегнетоэлектрика исчезает, называют коэрцитивной силой.

Если внешнее поле противоположного направления продолжать увеличивать, то через некоторое время наступает насыщение (кривая 2). При циклическом изменении внешнего поля получается замкнутая линия, называемая петлей гистерезиса.

5.Для сегнетоэлектрика существует температура, выше которой он теряет свои необычные свойства и превращается в обычный диэлектрик. Она получила название температуры Кюри . Для сегнетовой соли, которая дала название этой группе диэлектриков, существует две температуры Кюри С и С, выше и ниже этих температур он превращается в обычный диэлектрик.

Высокие значения относительной диэлектрической проницаемости позволяют использовать сегнетоэлектрики в качестве материалов для конденсаторов высокой удельной емкости. Нелинейная зависимость модуля вектора поляризации от напряженности внешнего поля находит применение при изготовлении нелинейных конденсаторов - варикондах, которые используются в системах автоматического контроля и управления.